
高校数学をプログラミングで解く(数学II編)「5-1 微分係数、導関数」
マガジンリスト > 数学Ⅱ編 5.微分法と積分法 > 5-1 微分係数、導関数
はじめに
今回は、数学IIで学ぶ「微分係数、導関数」について、微分係数や導関数をコンピュータで近似的に計算する3つの方法を紹介し、それらの結果の精度について比較するためのプログラムを作成します。
微分係数、導関数
まず、微分係数や導関数などについて解説しておきます。
平均変化率
$$
\frac{f(b)-f(a)}{b-a}
$$
微分係数(変化率)
$$
f'(a) = \lim_{h \to 0} \frac{f(a+h)-f(a)}{h} = \lim_{b \to a} \frac{f(b)-f(a)}{b-a}
$$
導関数
$$
f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}
$$
導関数の公式
① $${n}$$が正の整数のとき $${(x^n)'=n x^{n-1}}$$
② $${c}$$が定数のとき $${(c)' = 0}$$
③ $${k,l}$$が定数のとき $${ \{kf(x)+lg(x) \}' = kf'(x)+lg'(x) }$$
コンピュータで微分する(数値微分)
上記で、微分係数や導関数について解説しましたが、この微分をコンピュータで行うためには1つ問題があります。それは、$${h \to 0}$$や$${b \to a}$$などの極限処理をコンピュータで行うことができないことです。つまり、微分係数や導関数をコンピュータで厳密に計算することは難しいです。そこで、コンピュータで微分する場合、差分という処理で近似します。考え方は単純で、$${h \to 0}$$のような極限を取る代わりに、小さな正の値をもつ$${h (\ll 1)}$$に対して、
$$
\frac{f(a+h)-f(a)}{h} \mathrm{や} \frac{f(x+h)-f(x)}{h}
$$
を計算することで微分係数や導関数を近似するということを行います。この処理を数値微分と呼びます。
数値微分の方法としては、大きく3つの方法があります。順に紹介していきます。
前方差分
1つ目は前方差分です。
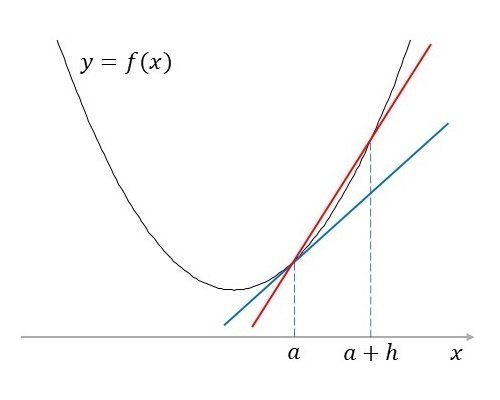
図1を見てください。青色の直線は関数$${f(x)}$$の$${x=a}$$での接線で、この接線の傾きが$${x=a}$$での微分係数$${f'(a)}$$となります。この微分係数$${f'(a)}$$を求めたいのですが、先ほども説明した通り、コンピュータでの極限処理が難しいので、厳密に$${f'(a)}$$を求めることはできません。
そこで、赤色の直線のように、$${x=a}$$での$${y=f(x)}$$のグラフ上の点$${(a, f(a))}$$と$${x=a}$$より少し前方の$${x=a+h}$$での点$${(a+h, f(a+h))}$$と結ぶ直線を考え、その直線の傾きを$${f'(a)}$$の近似値とします。
$$
f'(a) \approx \frac{f(a+h)-f(a)}{h}
$$
これを前方差分と呼びます。
後方差分
次に、後方差分です。
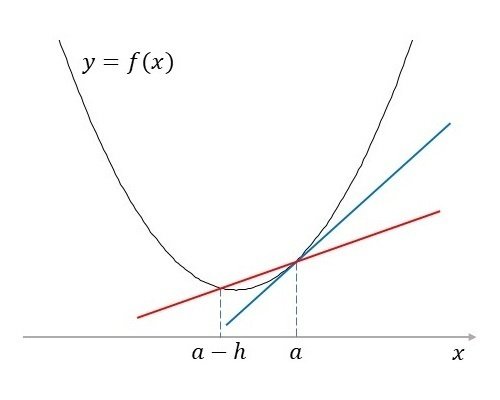
図2の赤色の直線を見てください。$${x=a}$$での$${y=f(x)}$$のグラフ上の点$${(a, f(a))}$$と$${x=a}$$より少し後方の$${x=a-h}$$での点$${(a-h, f(a-h))}$$と結ぶ直線を考え、その直線の傾きを$${f'(a)}$$の近似値とします。
$$
f'(a) \approx \frac{f(a)-f(a-h)}{h}
$$
これを後方差分と呼びます。
中心差分
最後は、中心差分です。
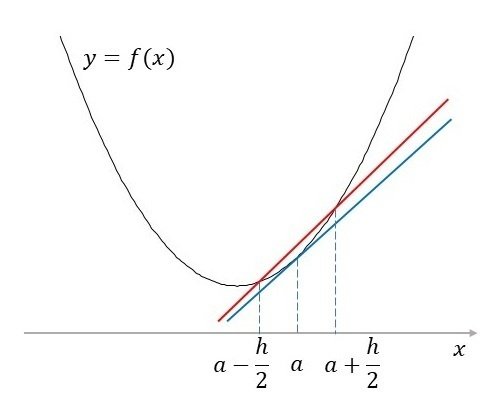
図3の赤色の直線を見てください。$${x=a}$$より少し後方の$${x=a-h/2}$$での点$${(a-h/2, f(a-h/2))}$$と$${x=a}$$より少し前方の$${x=a+h/2}$$での点$${(a+h/2, f(a+h/2))}$$と結ぶ直線を考え、その直線の傾きを$${f'(a)}$$の近似値とします。
$$
f'(a) \approx \frac{f(a+h/2)-f(a-h/2)}{h}
$$
これを後方差分と呼びます。
以下で、これら3つの方法の精度について比較してみます。
数値微分を比較してみる
以下の問題を考えます。
問題
$${f(x)=3x^2+2x+1}$$について、次の値を求めよ。
(1) $${f'(0)}$$
(2) $${f'(1)}$$
(3) $${f'(-1)}$$
(4) $${f'(2)}$$
問題の解法
この問題は、
$$
f'(x) = 6x+2
$$
となりますので、問題の値はそれぞれ (1) $${2}$$, (2) $${8}$$, (3) $${-4}$$, (4) $${14}$$と解析的に求めることができます。この結果と、3つの方法で求めた数値微分の結果を比較して、数値微分の精度について考察してみます。
プログラム
微分係数の真値と3つの数値微分の結果を比較するためのプログラムを作成します。
// 数値微分の精度比較
void setup(){
float h = 0.001; // 差分の大きさ
// (1) f'(0)
float a = 0.0;
float exact = f_prime(a);
float front = front_diff(a,h);
float back = back_diff(a,h);
float central = central_diff(a,h);
println("(1):", exact, "前方差分:", front, "後方差分:", back, "中心差分:", central);
// (2) f'(1)
a = 1.0;
exact = f_prime(a);
front = front_diff(a,h);
back = back_diff(a,h);
central = central_diff(a,h);
println("(2):", exact, "前方差分:", front, "後方差分:", back, "中心差分:", central);
// (3) f'(-1)
a = -1.0;
exact = f_prime(a);
front = front_diff(a,h);
back = back_diff(a,h);
central = central_diff(a,h);
println("(3):", exact, "前方差分:", front, "後方差分:", back, "中心差分:", central);
// (4) f'(2)
a = 2.0;
exact = f_prime(a);
front = front_diff(a,h);
back = back_diff(a,h);
central = central_diff(a,h);
println("(4):", exact, "前方差分:", front, "後方差分:", back, "中心差分:", central);
}
// f(x) =3x^2+2x+1
float f(
float x
){
return 3.0*x*x+2.0*x+1.0;
}
// f'(x) = 6x+2
float f_prime(
float x
){
return 6.0*x+2.0;
}
// 前方差分
float front_diff(
float a,
float h // 差分の大きさ
){
return (f(a+h)-f(a))/h;
}
// 後方差分
float back_diff(
float a,
float h // 差分の大きさ
){
return (f(a)-f(a-h))/h;
}
// 中心差分
float central_diff(
float a,
float h // 差分の大きさ
){
return (f(a+h/2.0)-f(a-h/2.0))/h;
}ソースコード1 微分係数の真値と3つの数値微分の結果を比較するためのプログラム
ソースコード1では、問題となっている関数$${f(x)=3x^2+2x+1}$$とその導関数$${f'(x) = 6x+2}$$をそれぞれ関数名 f と f_prime として定義し、その関数 f を利用して、前方差分の関数 front_diff 、後方差分の関数 back_diff 、中心差分の関数 central_diff を準備しました。なお、3つの差分の関数それぞれの引数に、差分の大きさを表す$${h}$$を導入して、差分の大きさを調整できるようにしました。
ソースコード1を、Processingの開発環境ウィンドウを開いて(スケッチ名を「calcThreeDifferences」としています)、テキストエディタ部分に書いて実行します。

図4のように、コンソールに各微分係数の値がそれぞれ真値、前方差分、後方差分、中心差分の順に出力されます。
(1): 2.0 前方差分: 2.0029545 後方差分: 1.9969939 中心差分: 2.0000339
(2): 8.0 前方差分: 8.003235 後方差分: 7.9970355 中心差分: 8.000374
(3): -4.0 前方差分: -3.996968 後方差分: -4.0032864 中心差分: -4.0000677
(4): 14.0 前方差分: 14.001845 後方差分: 13.998031 中心差分: 13.999938
今回、$${h=0.001}$$として計算した結果、数値微分としては中心差分が一番精度よく近似できていることがわかります。
まとめ
今回は、数学IIで学ぶ「微分係数、導関数」について、微分係数や導関数をコンピュータで近似的に計算する3つの方法を紹介し、それらの結果の精度について比較するためのプログラムを作成しました。
コンピュータでは、極限処理ができないため、厳密な意味での微分はできません。そこで、数値微分と呼ばれる差分の形で微分係数や導関数を近似的に求めます。差分の方法は、前方差分、後方差分、中心差分の3つの方法を紹介しました。
なお、今回の問題では、中心差分がよい精度で近似できていましたが、関数$${f(x)}$$や$${h}$$の大きさの取り方によっては精度が変わってきます。どういう関数のときにどのような$${h}$$の値を利用してどのような差分の方法がいいのか、など一度試しておくと数値計算の理解の助けになると思いますので、是非いろいろと試してみてください。
参考文献
改訂版 教科書傍用 スタンダード 数学II(数研出版、ISBN9784410209369)
