
高校数学をプログラミングで解く(数学I編)「1-3 平行移動、対称移動」
マガジンリスト > 数学Ⅰ編 1.2次関数 > 1-3 平行移動、対称移動
はじめに
今回は、数学Iで学ぶ「平行移動、対称移動」について、2次関数のグラフとともにその2次関数のグラフを平行移動したものや対称移動したものを描くプログラムを作成します。
2次関数(標準形)のグラフを描く
記事『高校数学をプログラミングで解く(数学I編)「1-2 2次関数のグラフ」』では、2次関数の一般形$${y=ax^2+bx+c}$$のグラフを描くプログラムを作成しました。今回は、2次関数の標準形
$$
y=a(x-p)^2+q (a \neq 0)
$$
を関数化して、2次関数のグラフを描くプログラムを準備しておきます。なお、2次関数を標準形で表した場合、2次関数の軸が直線$${x=p}$$、2次関数の頂点が点$${(p,q)}$$となります。
2次関数(標準形)のプログラム
2次関数の標準形のプログラムは以下のようになります。
// 2次関数の標準形
float quadraticfunction(
float a, // 2次の係数
float p, // 2次関数の軸
float q, // 頂点のy座標
float x
){
return a*(x-p)*(x-p) + q;
}今回は2次関数の標準形の係数やパラメータ$${a,p,q}$$をプログラムの関数の引数として与えています。
2次関数(標準形)を描くプログラム
上記の2次関数の標準形のプログラムを利用して、2次関数のグラフを描くプログラムを作成します。なお、今回は
$$
a=1, \ p=2, \ q=2
$$
として2次関数
$$
y=(x-2)^2+2
$$
のグラフを描きます。つまり、頂点が第1象限にくる、下に凸の2次関数のグラフを描きます。
// 2次関数の標準形y=a(x-p)^2+qのグラフを描く
void setup(){
size(500,500);
noLoop();
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
setAxes(x_range, y_range); // 座標軸の準備
noFill();
stroke(0,0,0);
// グラフの定義域
float x_l = -x_range; // 定義域の左端
float x_r = x_range; // 定義域の右端
int plot_num = 200; // グラフを描くための頂点の個数
// 2次関数(標準形)の係数
float a = 1.0;
float p = 2.0;
float q = 2.0;
// グラフを描画
float x, y; // 関数の座標
float X, Y; // キャンバス上の座標
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_l + (x_r - x_l) / plot_num * i; // 関数のx座標
y = quadraticfunction(a, p, q, x); // 関数の値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
// 軸と頂点をキャンバス上の座標に変換
float P, Q;
P = width / 2.0 / x_range * p;
Q = height / 2.0 / y_range * q;
// 2次関数の軸を描画
stroke(0,0,255);
line(P, -height/2.0, P, height/2.0);
// 2次関数の頂点を描画
stroke(255,0,0);
strokeWeight(5);
point(P, Q);
}
// 2次関数の標準形
float quadraticfunction(
float a, // 2次の係数
float p, // 2次関数の軸
float q, // 頂点のy座標
float x
){
return a*(x-p)*(x-p) + q;
}ソースコード1 2次関数の標準形$${y=a(x-p)^2+q}$$を描くプログラム
プログラムは、記事『高校数学をプログラミングで解く(数学I編)「1-0-2 グラフを描くための準備(その2)」』で作成したスケッチ「drawFunction」を再利用します。以下の zip ファイルをダウンロードして展開または解凍してください。
そして、スケッチの名前(フォルダ名)を「drawQuadraticFunctionVertexForm」と変更し、またスケッチ「drawQuadraticFunctionVertexForm」内の「drawFunction.pde」ファイルの名前を「drawQuadraticFunctionVertexForm.pde」に変更します。そして、pdeファイル「drawQuadraticFunctionVertexForm.pde」をダブルクリックしてスケッチ「drawQuadraticFunctionVertexForm」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「drawQuadraticFunctionVertexForm」タブを選択し、そのテキストエリアのソースコードを上記のソースコード1で書き換えます。
このプログラムを実行すると、図1のように、実行ウィンドウのキャンバスに2次関数のグラフが描かれます。
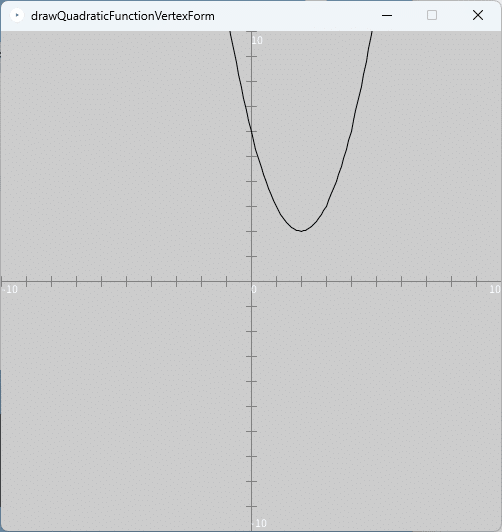
以下ではこの2次関数のグラフを平行移動や対称移動したグラフを描くプログラムについて説明していきます。
2次関数を平行移動する
ではまず、2次関数を平行移動するプログラムを作成していきます。
グラフの平行移動
一般に、$${x}$$軸方向に$${\Delta p}$$、$${y}$$軸方向に$${\Delta q}$$だけグラフを平行移動するとき、そのグラフの関数$${y=f(x)}$$は、
$$
y=f(x) \ \ \longrightarrow \ \ y=f(x- \Delta p)+\Delta q
$$
に変更されます。
グラフを平行移動するプログラム
それでは、ベースとなる2次関数のグラフとともにそのグラフを平行移動したグラフを描くプログラムを作成します。今回は平行移動の大きさとして、
$$
\Delta p= -4, \ \Delta q = 1
$$
とします。また、プログラムでは、$${\Delta p}$$を float 型の変数 dp 、$${\Delta q}$$を float 型の変数 dq としています。
// 2次関数の標準形y=a(x-p)^2+qのグラフを平行移動する
void setup(){
size(500,500);
noLoop();
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
setAxes(x_range, y_range); // 座標軸の準備
noFill();
stroke(0,0,0);
// グラフの定義域
float x_l = -x_range; // 定義域の左端
float x_r = x_range; // 定義域の右端
int plot_num = 200; // グラフを描くための頂点の個数
// 2次関数(標準形)の係数
float a = 1.0;
float p = 2.0;
float q = 2.0;
// グラフを描画
float x, y; // 関数の座標
float X, Y; // キャンバス上の座標
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_l + (x_r - x_l) / plot_num * i; // 関数のx座標
y = quadraticfunction(a, p, q, x); // 関数の値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
// 平行移動したグラフを描く
float dp = -4.0;
float dq = 1.0;
stroke(0,0,255); // 輪郭を青色にする
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_l + (x_r - x_l) / plot_num * i; // 関数のx座標
y = quadraticfunction(a, p, q, x-dp) + dq; // 平行移動した関数の値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
}
// 2次関数の標準形
float quadraticfunction(
float a, // 2次の係数
float p, // 2次関数の軸
float q, // 頂点のy座標
float x
){
return a*(x-p)*(x-p) + q;
}ソースコード2 平行移動した2次関数のグラフを描くプログラム
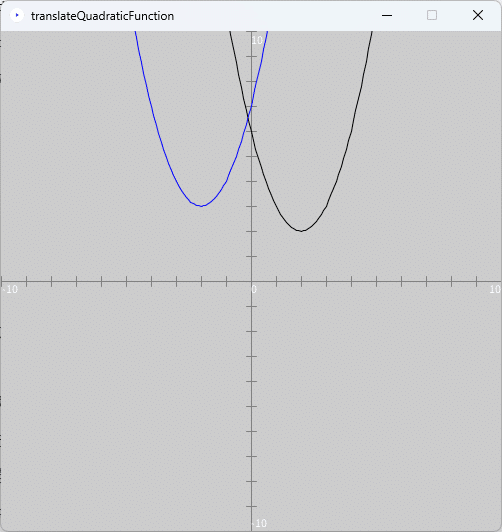
スケッチ「drawQuadraticFunctionVertexForm」をコピーして、そのスケッチ名を「translateQuadraticFunction」に変更し、またスケッチ「translateQuadraticFunction」内の「drawQuadraticFunctionVertexForm.pde」ファイルの名前を「translateQuadraticFunction.pde」に変更します。そして、pdeファイル「translateQuadraticFunction.pde」をダブルクリックしてスケッチ「translateQuadraticFunction」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「translateQuadraticFunction」タブを選択し、そのテキストエリアのソースコードを上記のソースコード2で書き換えます。このプログラムを実行すると、図2のように、実行ウィンドウのキャンバスに2次関数のグラフとそれを平行移動したグラフ(青色のグラフ)が描かれます。
実際、2次関数の頂点に注目すると、平行移動した2次関数(青色のグラフ)の頂点$${(-2,3)}$$が、ベースとなる2次関数(黒色のグラフ)の頂点$${(2,2)}$$を、$${x}$$軸方向に$${-4}$$、$${y}$$軸方向に$${1}$$だけ平行移動した点となっており、正しく平行移動されていることがわかります。
プログラムの解説
ソースコード2は、ソースコード1に対して、以下の平行移動したグラフを描くためのプログラムを追記しているだけです。
// 平行移動したグラフを描く
float dp = -4.0;
float dq = 1.0;
stroke(0,0,255); // 輪郭を青色にする
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_l + (x_r - x_l) / plot_num * i; // 関数のx座標
y = quadraticfunction(a, p, q, x-dp) + dq; // 平行移動した関数の値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();このプログラムの
y = quadraticfunction(a, p, q, x-dp) + dq; // 平行移動した関数の値に注目すると、これはベースとなる2次関数の関数 quadraticfunction を平行移動
$$
y=f(x) \ \ \longrightarrow \ \ y=f(x- \Delta p)+\Delta q
$$
の通りに変形しただけになっていることがわかります。
なお、この変形は今回2次関数を標準形に表したことで、
$$
\begin{array}{l}
y=a(x-p)^2+q \\ \longrightarrow \ \ y=a(x-p- \Delta p)^2+q+\Delta q=a(x-(p+ \Delta p))^2+(q+\Delta q)
\end{array}
$$
となるので、プログラムで
y = quadraticfunction(a, p+dp, q+dq, x); // 平行移動した関数の値としても同じ結果が得られます。
2次関数をx軸に関して対称移動する
次は、2次関数を$${x}$$軸に関して対称移動するプログラムを作成していきます。
グラフをx軸に関して対称移動
一般に、グラフを$${x}$$軸に関して対称移動するとき、そのグラフの関数$${y=f(x)}$$は、
$$
y=f(x) \ \ \longrightarrow \ \ y=-f(x)
$$
となります。
グラフをx軸に関して対称移動するプログラム
ベースとなる2次関数のグラフとともにそのグラフを$${x}$$軸に関して対称移動したグラフを描くプログラムを作成します。
// 2次関数の標準形y=a(x-p)^2+qのグラフをx軸に関して対称移動する
void setup(){
size(500,500);
noLoop();
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
setAxes(x_range, y_range); // 座標軸の準備
noFill();
stroke(0,0,0);
// グラフの定義域
float x_l = -x_range; // 定義域の左端
float x_r = x_range; // 定義域の右端
int plot_num = 200; // グラフを描くための頂点の個数
// 2次関数(標準形)の係数
float a = 1.0;
float p = 2.0;
float q = 2.0;
// グラフを描画
float x, y; // 関数の座標
float X, Y; // キャンバス上の座標
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_l + (x_r - x_l) / plot_num * i; // 関数のx座標
y = quadraticfunction(a, p, q, x); // 関数の値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
// x軸に関して対称移動したグラフを描く
stroke(0,0,255); // 輪郭を青色にする
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_l + (x_r - x_l) / plot_num * i; // 関数のx座標
y = -quadraticfunction(a, p, q, x); // x軸に関して対称移動した関数の値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
}
// 2次関数の標準形
float quadraticfunction(
float a, // 2次の係数
float p, // 2次関数の軸
float q, // 頂点のy座標
float x
){
return a*(x-p)*(x-p) + q;
}ソースコード3 $${x}$$軸に関して対称移動したグラフを描くプログラム
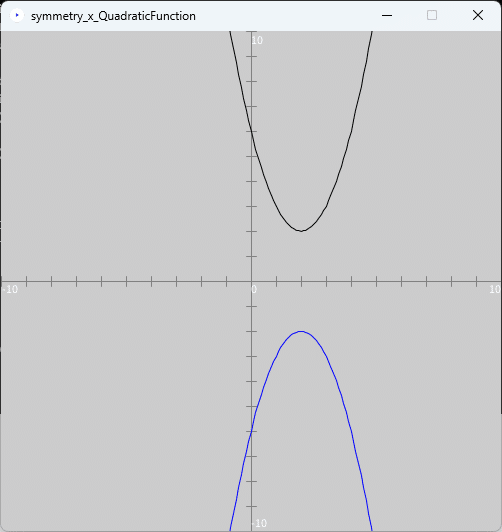
スケッチ「drawQuadraticFunctionVertexForm」をコピーして、そのスケッチ名を「symmetry_x_QuadraticFunction」に変更し、またスケッチ「symmetry_x_QuadraticFunction」内の「drawQuadraticFunctionVertexForm.pde」ファイルの名前を「symmetry_x_QuadraticFunction.pde」に変更します。そして、pdeファイル「symmetry_x_QuadraticFunction.pde」をダブルクリックしてスケッチ「symmetry_x_QuadraticFunction」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「symmetry_x_QuadraticFunction」タブを選択し、そのテキストエリアのソースコードを上記のソースコード3で書き換えます。このプログラムを実行すると、図3のように、実行ウィンドウのキャンバスに2次関数のグラフとそれを$${x}$$軸に関して対称移動したグラフ(青色のグラフ)が描かれます。
プログラムの解説
ソースコード3は、ソースコード1に対して、以下の$${x}$$軸に関して対称移動したグラフを描くためのプログラムを追記しているだけです。
// x軸に関して対称移動したグラフを描く
stroke(0,0,255); // 輪郭を青色にする
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_l + (x_r - x_l) / plot_num * i; // 関数のx座標
y = -quadraticfunction(a, p, q, x); // x軸に関して対称移動した関数の値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();このプログラムの
y = -quadraticfunction(a, p, q, x); // x軸に関して対称移動した関数の値に注目すると、これはベースとなる2次関数の関数 quadraticfunction を$${x}$$軸に関する対称移動
$$
y=f(x) \ \ \longrightarrow \ \ y=-f(x)
$$
の通りに変形しただけになっていることがわかります。
2次関数をy軸に関して対称移動する
次は、2次関数を$${y}$$軸に関して対称移動するプログラムを作成していきます。
グラフをy軸に関して対称移動
一般に、グラフを$${y}$$軸に関して対称移動するとき、そのグラフの関数$${y=f(x)}$$は、
$$
y=f(x) \ \ \longrightarrow \ \ y=f(-x)
$$
となります。
グラフをy軸に関して対称移動するプログラム
ベースとなる2次関数のグラフとともにそのグラフを$${y}$$軸に関して対称移動したグラフを描くプログラムを作成します。
// 2次関数の標準形y=a(x-p)^2+qのグラフをy軸に関して対称移動する
void setup(){
size(500,500);
noLoop();
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
setAxes(x_range, y_range); // 座標軸の準備
noFill();
stroke(0,0,0);
// グラフの定義域
float x_l = -x_range; // 定義域の左端
float x_r = x_range; // 定義域の右端
int plot_num = 200; // グラフを描くための頂点の個数
// 2次関数(標準形)の係数
float a = 1.0;
float p = 2.0;
float q = 2.0;
// グラフを描画
float x, y; // 関数の座標
float X, Y; // キャンバス上の座標
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_l + (x_r - x_l) / plot_num * i; // 関数のx座標
y = quadraticfunction(a, p, q, x); // 関数の値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
// y軸に関して対称移動したグラフを描く
stroke(0,0,255); // 輪郭を青色にする
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_l + (x_r - x_l) / plot_num * i; // 関数のx座標
y = quadraticfunction(a, p, q, -x); // y軸に関して対称移動した関数の値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
}
// 2次関数の標準形
float quadraticfunction(
float a, // 2次の係数
float p, // 2次関数の軸
float q, // 頂点のy座標
float x
){
return a*(x-p)*(x-p) + q;
}ソースコード4 $${y}$$軸に関して対称移動したグラフを描くプログラム
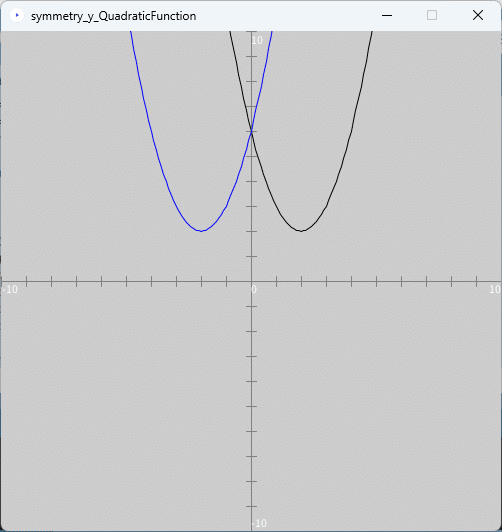
スケッチ「drawQuadraticFunctionVertexForm」をコピーして、そのスケッチ名を「symmetry_y_QuadraticFunction」に変更し、またスケッチ「symmetry_y_QuadraticFunction」内の「drawQuadraticFunctionVertexForm.pde」ファイルの名前を「symmetry_y_QuadraticFunction.pde」に変更します。そして、pdeファイル「symmetry_y_QuadraticFunction.pde」をダブルクリックしてスケッチ「symmetry_y_QuadraticFunction」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「symmetry_y_QuadraticFunction」タブを選択し、そのテキストエリアのソースコードを上記のソースコード4で書き換えます。このプログラムを実行すると、図4のように、実行ウィンドウのキャンバスに2次関数のグラフとそれを$${y}$$軸に関して対称移動したグラフ(青色のグラフ)が描かれます。
プログラムの解説
ソースコード4は、ソースコード1に対して、以下の$${y}$$軸に関して対称移動したグラフを描くためのプログラムを追記しているだけです。
// y軸に関して対称移動したグラフを描く
stroke(0,0,255); // 輪郭を青色にする
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_l + (x_r - x_l) / plot_num * i; // 関数のx座標
y = quadraticfunction(a, p, q, -x); // y軸に関して対称移動した関数の値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();このプログラムの
y = quadraticfunction(a, p, q, -x); // y軸に関して対称移動した関数の値に注目すると、これはベースとなる2次関数の関数 quadraticfunction を$${y}$$軸に関する対称移動
$$
y=f(x) \ \ \longrightarrow \ \ y=f(-x)
$$
の通りに変形しただけになっていることがわかります。
2次関数を原点に関して対称移動する
次は、2次関数を原点に関して対称移動するプログラムを作成していきます。
グラフを原点に関して対称移動
一般に、グラフを原点に関して対称移動するとき、そのグラフの関数$${y=f(x)}$$は、
$$
y=f(x) \ \ \longrightarrow \ \ y=-f(-x)
$$
となります。
グラフを原点に関して対称移動するプログラム
ベースとなる2次関数のグラフとともにそのグラフを原点に関して対称移動したグラフを描くプログラムを作成します。
// 2次関数の標準形y=a(x-p)^2+qのグラフを原点に関して対称移動する
void setup(){
size(500,500);
noLoop();
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
setAxes(x_range, y_range); // 座標軸の準備
noFill();
stroke(0,0,0);
// グラフの定義域
float x_l = -x_range; // 定義域の左端
float x_r = x_range; // 定義域の右端
int plot_num = 200; // グラフを描くための頂点の個数
// 2次関数(標準形)の係数
float a = 1.0;
float p = 2.0;
float q = 2.0;
// グラフを描画
float x, y; // 関数の座標
float X, Y; // キャンバス上の座標
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_l + (x_r - x_l) / plot_num * i; // 関数のx座標
y = quadraticfunction(a, p, q, x); // 関数の値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
// 原点に関して対称移動したグラフを描く
stroke(0,0,255); // 輪郭を青色にする
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_l + (x_r - x_l) / plot_num * i; // 関数のx座標
y = -quadraticfunction(a, p, q, -x); // 原点に関して対称移動した関数の値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
}
// 2次関数の標準形
float quadraticfunction(
float a, // 2次の係数
float p, // 2次関数の軸
float q, // 頂点のy座標
float x
){
return a*(x-p)*(x-p) + q;
}ソースコード5 原点に関して対称移動したグラフを描くプログラム
スケッチ「drawQuadraticFunctionVertexForm」をコピーして、そのスケッチ名を「symmetry_origin_QuadraticFunction」に変更し、またスケッチ「symmetry_origin_QuadraticFunction」内の「drawQuadraticFunctionVertexForm.pde」ファイルの名前を「symmetry_origin_QuadraticFunction.pde」に変更します。そして、pdeファイル「symmetry_origin_QuadraticFunction.pde」をダブルクリックしてスケッチ「symmetry_origin_QuadraticFunction」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「symmetry_origin_QuadraticFunction」タブを選択し、そのテキストエリアのソースコードを上記のソースコード5で書き換えます。このプログラムを実行すると、図5のように、実行ウィンドウのキャンバスに2次関数のグラフとそれを原点に関して対称移動したグラフ(青色のグラフ)が描かれます。

プログラムの解説
ソースコード5は、ソースコード1に対して、以下の原点に関して対称移動したグラフを描くためのプログラムを追記しているだけです。
// 原点に関して対称移動したグラフを描く
stroke(0,0,255); // 輪郭を青色にする
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_l + (x_r - x_l) / plot_num * i; // 関数のx座標
y = -quadraticfunction(a, p, q, -x); // 原点に関して対称移動した関数の値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();このプログラムの
y = -quadraticfunction(a, p, q, -x); // 原点に関して対称移動した関数の値に注目すると、これはベースとなる2次関数の関数 quadraticfunction を原点に関する対称移動
$$
y=f(x) \ \ \longrightarrow \ \ y=-f(-x)
$$
の通りに変形しただけになっていることがわかります。
まとめ
今回は、数学Iで学ぶ「平行移動、対称移動」について、2次関数のグラフとともにその2次関数のグラフを平行移動したものや対称移動したものを描くプログラムを作成しました。
平行移動や対称移動したグラフを描くことは比較的簡単で、ベースとなるグラフの関数に対して平行移動や対称移動する変形を行った関数を用意してそれをグラフとして描くだけになります。
今回のポイントとしては、平行移動や対称移動を行ったグラフを描く際に、関数 quadraticfunction の中身を一切変更せず、関数 quadraticfunction を再利用していることです。実際変更したのは、関数 quadraticfunction を呼び出す際に引数$${x}$$を$${x-\Delta p}$$や$${-x}$$に変えただけです。
今回のように、プログラムの関数をうまく再利用していくことは、プログラムを簡潔に書くことや、メンテナンス性にも優れたプログラムを書くことに役に立ちます。少しずつこのような書き方に慣れていってください。
読んだ感想などをお寄せください
本記事を読んだ感想や質問などを以下のお問い合せフォームからお寄せください。感想、質問をいただいた方には本記事の演習問題の解答をプレゼントします。(お問合せフォームの本文に、本記事のタイトルを入れてください。)
参考文献
改訂版 教科書傍用 スタンダード 数学I(数研出版、ISBN9784410209178)
演習問題
2次関数
$$
y=\frac{1}{2}(x-4)^2+3
$$
のグラフ(黒色)に対して、
・原点が頂点になるように平行移動したグラフ(赤色)
・$${x}$$軸に関して対称移動したグラフ(緑色)
・$${y}$$軸に関して対称移動したグラフ(青色)
・原点に関して対称移動したグラフ(黄色)
を描くプログラムを作成してください。
演習問題の解答例
ここから先は
この記事が気に入ったらチップで応援してみませんか?
