
高校数学をプログラミングで解く(数学II編)「2-6 不等式の表す領域」
マガジンリスト > 数学Ⅱ編 2.図形と方程式 > 2-6 不等式の表す領域
はじめに
今回は、数学IIで学ぶ「不等式の表す領域」について、与えられた不等式の条件を満たす点をプロットしていくことで不等式の表す領域を描いていくプログラムを作成します。
不等式の表す領域
まず、不等式の表す領域について解説しておきます。
曲線を境界線とする領域
① $${y > f(x)}$$の表す領域は曲線$${y=f(x)}$$の上側の部分
② $${y < f(x)}$$の表す領域は曲線$${y=f(x)}$$の下側の部分
※注意 $${y \geq f(x), \ y \leq f(x)}$$の表す領域は、境界線$${y=f(x)}$$も含む領域になる。
円と領域
円$${(x-a)^2+(y-b)^2 = r^2}$$を$${C}$$とする。
① $${(x-a)^2+(y-b)^2 < r^2}$$の表す領域は、円$${C}$$の内部
② $${(x-a)^2+(y-b)^2 > r^2}$$の表す領域は、円$${C}$$の外部
領域を利用した証明法
2つの条件$${p, q}$$が$${x,y}$$の不等式で表されていて、命題$${ p \Rightarrow q }$$が真であることを証明する場合、$${(p \mathrm{の表す領域}) \subset (q \mathrm{の表す領域})}$$が成り立つことを示せばよい。
不等式の表す領域を描く
今回は、不等式の表す領域を描くプログラムを作成していきます。
問題
次の不等式の表す領域を図示せよ。
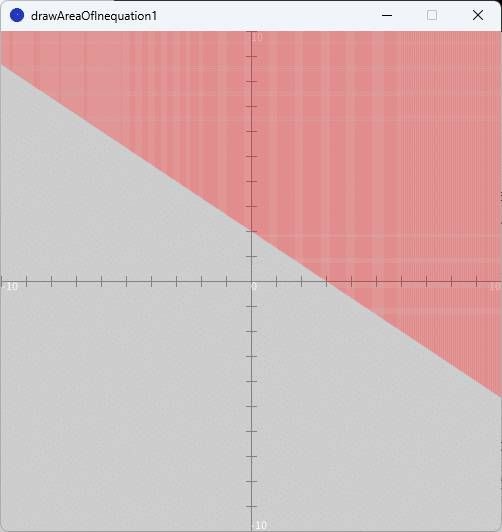
(1) $${2x+3y-6 \geq 0}$$
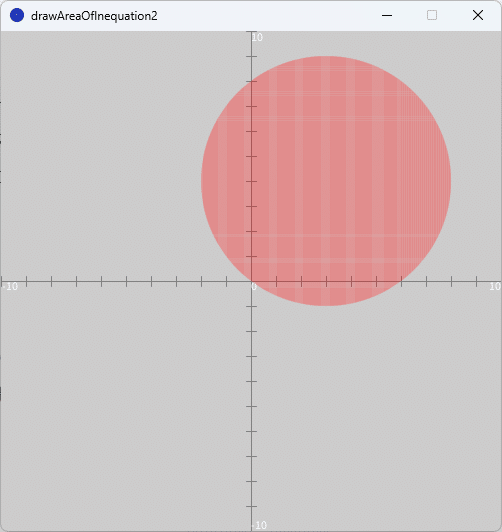
(2) $${x^2+y^2-6x-8y \leq 0}$$
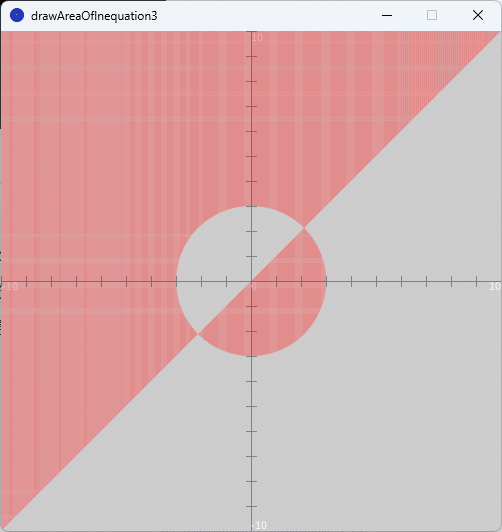
(3) $${(y-x)(x^2+y^2-9) >0}$$
アルゴリズム設計
今回は不等式の表す領域を次のような手順で描くことにします。

① 図1のようにキャンバスの描画範囲内に刻み幅 pitch の間隔で点をとります。
② それらのすべての点の座標$${(x,y)}$$に対して条件の不等式を満たすかどうかを確かめていきます。
②-1 条件の不等式が$${y > f(x)}$$の場合、この条件を満たしていればその点(図1の青色)をキャンバス上にプロットし、条件を満たしていなければプロットしないことで、プロットされた領域が不等式$${y > f(x)}$$の表す領域となります。
②-2 条件の不等式が$${y < f(x)}$$の場合、この条件を満たしていればその点(図1の赤色)をキャンバス上にプロットし、条件を満たしていなければプロットしないことで、プロットされた領域が不等式$${y < f(x)}$$の表す領域となります。
②-3 条件の不等式に等号が含まれる場合、境界線$${y=f(x)}$$の条件を満たす点(図1の黒色)も一緒にプロットします。
問題(1)のプログラム
それでは、問題(1)の不等式の表す領域を描くプログラムを作成します。今回は、setAxes.pdeファイルと座標$${(x,y)}$$に点をプロットする関数 plot_point を再利用したいので、記事『高校数学をプログラミングで解く(数学II編)「2-3 円の方程式」』で作成したスケッチ「drawCircles」を再利用します。スケッチ「drawCircles」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「drawAreaOfInequation1」と変更し、またスケッチ「drawAreaOfInequation1」内の「drawCircles.pde」ファイルの名前を「drawAreaOfInequation1.pde」に変更します。そして、pdeファイル「drawAreaOfInequation1.pde」をダブルクリックしてスケッチ「drawAreaOfInequation1」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「drawAreaOfInequation1」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500);
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill();
stroke(255,0,0,5);
// 刻み幅
float pitch = 0.01;
// plot数
int plot_num = (int)(2 * x_range / pitch);
float x, y; // 任意の点の座標
for(int i=0; i<=plot_num; i++){
for(int j=0; j<=plot_num; j++){
x = -x_range + i * pitch;
y = -y_range + j * pitch;
if( function1(x,y) >= 0.0 ){
plot_point(x,y);
}
}
}
}
// 不等式に利用する関数
float function1(
float x,
float y
){
return 2.0*x+3.0*y-6.0;
}
// 座標(x,y)に点をプロットする関数
void plot_point(
float x, // 点のx座標
float y // 点のy座標
){
float X, Y; // キャンバス上の座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
// strokeWeight(5);
point(X, Y);
// strokeWeight(1);
}ソースコード1 問題(1)の不等式の表す領域を描くプログラム
今回、座標$${(x,y)}$$に点をプロットする関数 plot_point を再利用していますが、プロットする点のサイズは1つの画素サイズと同じにするために strokeWeight 関数は利用しないようにコメントアウトしています。また、ソースコード1の
if( function1(x,y) >= 0.0 ){
plot_point(x,y);
}の部分で、点の座標$${(x,y)}$$が不等式の条件を満たす場合のみ、その座標位置に点をプロットするようにしています。
ソースコード1を、スケッチ「drawAreaOfInequation1」の「drawAreaOfInequation1」タブのテキストエディタ部分に書いて実行すると、図2のように、実行ウィンドウのキャンバス上に問題(1)の不等式の表す領域が赤色の点群で描かれます。なお、$${x}$$軸や$${y}$$軸の表示範囲$${-10 \leq x,y \leq 10}$$に対して刻み幅 pitch を$${0.01}$$とかなり細かく設定したため、赤色の点群が描画された部分は赤色で塗りつぶされたように見えています。
問題(2)のプログラム
次に、問題(2)の不等式の表す領域を描くプログラムを作成します。先ほど作成したスケッチ「drawAreaOfInequation1」を再利用します。
スケッチ「drawAreaOfInequation1」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「drawAreaOfInequation2」と変更し、またスケッチ「drawAreaOfInequation2」内の「drawAreaOfInequation1.pde」ファイルの名前を「drawAreaOfInequation2.pde」に変更します。そして、pdeファイル「drawAreaOfInequation2.pde」をダブルクリックしてスケッチ「drawAreaOfInequation2」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「drawAreaOfInequation2」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500);
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill();
stroke(255,0,0,5);
// 刻み幅
float pitch = 0.01;
// plot数
int plot_num = (int)(2 * x_range / pitch);
float x, y; // 任意の点の座標
for(int i=0; i<=plot_num; i++){
for(int j=0; j<=plot_num; j++){
x = -x_range + i * pitch;
y = -y_range + j * pitch;
if( function2(x,y) <= 0.0 ){
plot_point(x,y);
}
}
}
}
// 不等式に利用する関数
float function2(
float x,
float y
){
return x*x+y*y-6.0*x-8.0*y;
}
// 座標(x,y)に点をプロットする関数
void plot_point(
float x, // 点のx座標
float y // 点のy座標
){
float X, Y; // キャンバス上の座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
// strokeWeight(5);
point(X, Y);
// strokeWeight(1);
}ソースコード2 問題(2)の不等式の表す領域を描くプログラム
ソースコード1との違いは、問題(2)に合わせて不等式に利用される関数 function2 を新たに定義したことと、点をプロットする条件を表す部分を
if( function2(x,y) <= 0.0 ){
plot_point(x,y);
}に変更したことになります。
ソースコード2を、スケッチ「drawAreaOfInequation2」の「drawAreaOfInequation2」タブのテキストエディタ部分に書いて実行すると、図3のように、実行ウィンドウのキャンバス上に問題(2)の不等式の表す領域が赤色の点群で描かれます。
問題(3)のプログラム
最後に、問題(3)の不等式の表す領域を描くプログラムを作成します。こちらもスケッチ「drawAreaOfInequation1」を再利用します。
スケッチ「drawAreaOfInequation1」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「drawAreaOfInequation3」と変更し、またスケッチ「drawAreaOfInequation3」内の「drawAreaOfInequation1.pde」ファイルの名前を「drawAreaOfInequation3.pde」に変更します。そして、pdeファイル「drawAreaOfInequation3.pde」をダブルクリックしてスケッチ「drawAreaOfInequation3」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「drawAreaOfInequation3」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500);
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill();
stroke(255,0,0,5);
// 刻み幅
float pitch = 0.01;
// plot数
int plot_num = (int)(2 * x_range / pitch);
float x, y; // 任意の点の座標
for(int i=0; i<=plot_num; i++){
for(int j=0; j<=plot_num; j++){
x = -x_range + i * pitch;
y = -y_range + j * pitch;
if( function3(x,y) > 0.0 ){
plot_point(x,y);
}
}
}
}
// 不等式に利用する関数
float function3(
float x,
float y
){
return (y-x)*(x*x+y*y-9.0);
}
// 座標(x,y)に点をプロットする関数
void plot_point(
float x, // 点のx座標
float y // 点のy座標
){
float X, Y; // キャンバス上の座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
// strokeWeight(5);
point(X, Y);
// strokeWeight(1);
}ソースコード3 問題(3)の不等式の表す領域を描くプログラム
ソースコード3を、スケッチ「drawAreaOfInequation3」の「drawAreaOfInequation3」タブのテキストエディタ部分に書いて実行すると、図4のように、実行ウィンドウのキャンバス上に問題(3)の不等式の表す領域が赤色の点群で描かれます。
まとめ
今回は、数学IIで学ぶ「不等式の表す領域」について、与えられた不等式の条件を満たす点をプロットしていくことで不等式の表す領域を描いていくプログラムを作成しました。
不等式の表す領域を描く方法として、今回はキャンバスの描画範囲内に等間隔で点を取り、それらのすべての点の座標$${(x,y)}$$が条件の不等式を満たしているかどうかを確認し、満たしていればその点をプロットし、満たしていなければプロットしないということを行うことで、描画された点群が不等式の表す領域となることを利用しました。
不等式の表す領域を描く方法については、もちろん他の方法もあります。例えば、ある程度解析的に(つまり式として)領域を分割しておいて最後にそれらの領域を塗りつぶすように図形を描画していくというものがあります。ちょっと手間がかかりそうですが、勉強にはなると思いますので、一度チャレンジしてみてください。
参考文献
改訂版 教科書傍用 スタンダード 数学II(数研出版、ISBN9784410209369)
この記事が気に入ったらサポートをしてみませんか?
