高校数学をプログラミングで解く（数学III編）「5-1 微分係数と導関数」

割引あり

MK's papa

2024年11月13日 05:32

マガジンリスト　＞　数学Ⅲ編 5.微分法　＞　5-1 微分係数と導関数

はじめに

今回は、数学IIIで学ぶ「微分係数と導関数」について、導関数の公式が正しく機能することを確認するためのプログラムを作成していきます。

微分係数と導関数

まず、導関数に関する種々の性質について解説しておきます。

微分可能と連続

関数$${f(x)}$$が$${x=a}$$で微分可能ならば、$${x=a}$$で連続。
注意　逆は不成立。

関数 f(x) の導関数

$$
f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}
$$

導関数の公式

$${f(x)}$$、$${g(x)}$$を微分可能な関数とする。

① 基本公式

$$
\{ kf(x) + lg(x) \}' = kf'(x) + lg'(x) \ \ \ \ (k,l\mathrm{は定数})
$$

② 積の導関数

$$
\{ f(x)g(x) \}' = f'(x) g(x) + f(x) g'(x)
$$

③ 商の導関数

$$
\left\{ \frac{f(x)}{g(x)} \right\}' = \frac{f'(x) g(x) - f(x) g'(x)}{ \{g(x)\}^2}
$$

④ 合成関数の導関数
$${y = f(u)}$$、$${u = g(x)}$$のとき、

$$
\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}
$$

⑤ 逆関数の導関数

$$
\frac{dy}{dx} = \frac{1}{ \frac{dx}{dy} }
$$

⑥ $${x^p}$$の導関数
$${p}$$が有理数（実数も可）のとき

$$
( x^p )' = p x^{p-1} \ \ \ \ (x > 0)
$$

導関数の公式を確かめる

今回は、上記で説明した②積の導関数、③商の導関数、④合成関数の導関数の公式が正しく機能することを確認するプログラムを作成していきます。

積の導関数の公式を確かめる

まず、②積の導関数の公式が正しく機能しているかを次の関数1を例にして考えていきます。

関数1

$$
y = (x^2+x)(x^4-2)
$$

アルゴリズム設計

① 導関数を算出するために関数を微分する必要があります。記事『高校数学をプログラミングで解く（数学II編）「5-1 微分係数、導関数」』で解説したように、コンピュータでの微分はその近似的な計算方法である数値微分を用います。特に、ここでは、前方差分を用いることにします。

② 今回は、積の導関数の公式を確かめることが目的ですので、関数1を次のように考えます。

$$
f(x) = x^2+x, \ \ \ \ g(x) = x^4-2
$$

$$
h(x) = f(x)g(x) = (x^2+x)(x^4-2)
$$

③ 関数$${f(x), g(x), h(x)}$$の導関数を前方差分を用いて求めます。

$$
f'(x) = \frac{f(x+\Delta x)-f(x)}{\Delta x}, \ \ \ \ g'(x) = \frac{g(x+\Delta x)-g(x)}{\Delta x}
$$

$$
h'(x) = \frac{h(x+\Delta x)-h(x)}{\Delta x}
$$

④ 最後に、これらの導関数を用いて、$${h'(x)}$$と$${f'(x)g(x)+f(x)g'(x)}$$のグラフを描きます。これらのグラフが一致すれば、積の導関数の公式が正しく機能していると考えることができます。

プログラム

それでは、積の導関数の公式が正しく機能しているかを確認するためのプログラムを作成していきます。

今回は、記事『高校数学をプログラミングで解く（数学I編）「1-0-2 グラフを描くための準備（その2）」』で作成したスケッチ「drawFunction」を再利用して作成していきます。以下の zip ファイルをダウンロードして展開または解凍してください。

そして、スケッチの名前（フォルダ名）を「check_product_formula」と変更し、またスケッチ「check_product_formula」内の「drawFunction.pde」ファイルの名前を「check_product_formula.pde」に変更します。そして、pdeファイル「check_product_formula.pde」をダブルクリックしてスケッチ「check_product_formula」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「check_product_formula」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。

float x_range = 5.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 5.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500);
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  noFill();
  
  // グラフの描画範囲  
  float x_min = -x_range;
  float x_max = x_range;
  
  // 導関数 dh のグラフを描く
  stroke(0,255,0);  
  strokeWeight(5);
  draw_dh(x_min, x_max);

  // 積の導関数 df g + f dg のグラフを描く
  stroke(255,0,0);
  strokeWeight(2);
  draw_product_formula(x_min, x_max);

}

// 関数 f(x)
float f(
  float x
){
  return x*x+x;
}

// 関数 g(x)
float g(
  float x
){
  return pow(x,4.0)-2.0;
}

// 関数 h(x)
float h(
  float x
){
  return f(x)*g(x);
}

// 関数 f(x) の導関数
float df(
  float x
){
  float dx = 0.001;
  return (f(x+dx)-f(x))/dx;
}

// 関数 g(x) の導関数
float dg(
  float x
){
  float dx = 0.001;
  return (g(x+dx)-g(x))/dx;
}

// 関数 h(x) の導関数
float dh(
  float x
){
  float dx = 0.001;
  return (h(x+dx)-h(x))/dx;
}

// 導関数 dh を描く関数
void draw_dh(
  float x_min, // グラフの定義域の下限
  float x_max  // グラフの定義域の上限
){
  int plot_num = 2000; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=1; i<plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // 曲線上の点のx座標
    y = dh(x); // 曲線上の点のyの値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

}

// 積の導関数 df g + f dg を描く関数
void draw_product_formula(
  float x_min, // グラフの定義域の下限
  float x_max  // グラフの定義域の上限
){
  int plot_num = 2000; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=1; i<plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // 曲線上の点のx座標
    y = df(x)*g(x)+f(x)*dg(x); // 曲線上の点のyの値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

}

ソースコード1　積の導関数の公式が正しく機能しているかを確認するためのプログラム

ソースコード1で、アルゴリズム設計で定義した関数$${f(x), g(x), h(x)}$$をそれぞれ f, g, h 関数として準備しています。また、これらの関数の導関数$${f'(x), g'(x), h'(x)}$$をそれぞれ df, dg, dh 関数として準備しています。なお、これらの導関数は前方差分を用いて算出しており、差分$${ \Delta x}$$は変数 dx = 0.001 で表しています。そして、導関数 dh と積の導関数 df g + f dg のグラフを描くための関数をそれぞれ draw_dh 関数と draw_product_formula 関数として準備し、これらの関数を setup 関数内で呼び出すことでグラフを描いています。

ソースコード1を、スケッチ「check_product_formula」の「check_product_formula」タブのテキストエディタ部分に書いて実行すると、図1のように、実行ウィンドウのキャンバス上に導関数$${h'(x)}$$のグラフが緑色の太線で、積の導関数$${f'(x)g(x)+f(x)g'(x)}$$のグラフが赤色の線でそれぞれ描かれます。

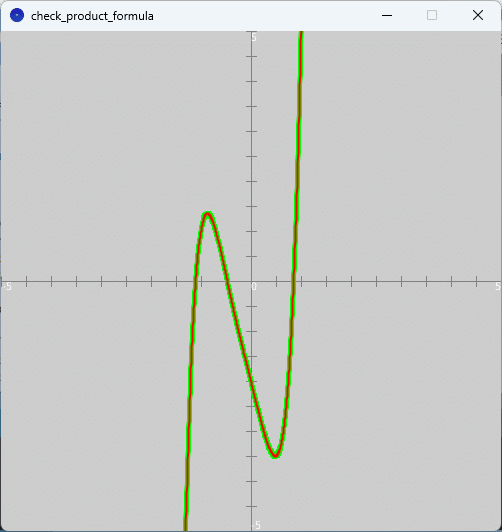
図1を見ると、導関数$${h'(x)}$$のグラフと積の導関数$${f'(x)g(x)+f(x)g'(x)}$$のグラフとが重なっています。つまり、これは積の導関数の公式が正しく機能していることを示唆しています。

商の導関数の公式を確かめる

次に、③商の導関数の公式が正しく機能しているかを次の関数2を例にして考えていきます。

関数2

$$
y = \frac{x}{x^2-x+1}
$$

アルゴリズム設計

基本的には、積の導関数の公式を確かめたときと同じやり方になります。
① 導関数は前方差分で計算することにします。

② 関数2を次のように考えます。

$$
f(x) = x, \ \ \ \ g(x) = x^2-x+1, \ \ \ \
h(x) = \frac{f(x)}{g(x)} = \frac{x}{x^2-x+1}
$$

③ 関数$${f(x), g(x), h(x)}$$の導関数$${f'(x), g'(x), h'(x)}$$を前方差分を用いて求めます。

④ 最後に、これらの導関数を用いて、$${h'(x)}$$と$${ \{ f'(x)g(x)-f(x)g'(x) \}/\{g(x)\}^2}$$のグラフを描きます。これらのグラフが一致すれば、商の導関数の公式が正しく機能していると考えることができます。

プログラム

それでは、商の導関数の公式が正しく機能しているかを確認するためのプログラムを作成していきます。

先程作成したスケッチ「check_product_formula」を再利用して作成していきます。
スケッチ「check_product_formula」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「check_quotient_formula」と変更し、またスケッチ「check_quotient_formula」内の「check_product_formula.pde」ファイルの名前を「check_quotient_formula.pde」に変更します。そして、pdeファイル「check_quotient_formula.pde」をダブルクリックしてスケッチ「check_quotient_formula」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「check_quotient_formula」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。

float x_range = 5.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 5.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500);
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  noFill();
  
  // グラフの描画範囲  
  float x_min = -x_range;
  float x_max = x_range;
  
  // 導関数 dh のグラフを描く
  stroke(0,255,0);  
  strokeWeight(5);
  draw_dh(x_min, x_max);

  // 商の導関数 (df g + f dg)/g^2 のグラフを描く
  stroke(255,0,0);
  strokeWeight(2);
  draw_quotient_formula(x_min, x_max);

}

// 関数 f(x)
float f(
  float x
){
  return x;
}

// 関数 g(x)
float g(
  float x
){
  return x*x-x+1.0;
}

// 関数 h(x)
float h(
  float x
){
  return f(x)/g(x);
}

// 関数 f(x) の導関数
float df(
  float x
){
  float dx = 0.001;
  return (f(x+dx)-f(x))/dx;
}

// 関数 g(x) の導関数
float dg(
  float x
){
  float dx = 0.001;
  return (g(x+dx)-g(x))/dx;
}

// 関数 h(x) の導関数
float dh(
  float x
){
  float dx = 0.001;
  return (h(x+dx)-h(x))/dx;
}

// 導関数 dh を描く関数
void draw_dh(
  float x_min, // グラフの定義域の下限
  float x_max  // グラフの定義域の上限
){
  int plot_num = 2000; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=1; i<plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // 曲線上の点のx座標
    y = dh(x); // 曲線上の点のyの値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

}

// 商の導関数 (df g + f dg)/g^2 を描く関数
void draw_quotient_formula(
  float x_min, // グラフの定義域の下限
  float x_max  // グラフの定義域の上限
){
  int plot_num = 2000; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=1; i<plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // 曲線上の点のx座標
    y = (df(x)*g(x)-f(x)*dg(x))/g(x)/g(x); // 曲線上の点のyの値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

}

ソースコード2　商の導関数の公式が正しく機能しているかを確認するためのプログラム

ソースコード2とソースコード1との違いは、関数 f と g とを問題2に合わせて書き換えた部分と、商の導関数 (df g - f dg)/g/g のグラフを描くための関数を draw_quotient_formula 関数として準備したところになります。

ソースコード2を、スケッチ「check_quotient_formula」の「check_quotient_formula」タブのテキストエディタ部分に書いて実行すると、図2のように、実行ウィンドウのキャンバス上に導関数$${h'(x)}$$のグラフが緑色の太線で、商の導関数$${ \{f'(x)g(x)+f(x)g'(x) \}/\{ g(x) \}^2}$$のグラフが赤色の線でそれぞれ描かれます。

図2を見ると、導関数$${h'(x)}$$のグラフと商の導関数$${ \{f'(x)g(x)+f(x)g'(x) \}/\{ g(x) \}^2}$$のグラフとが重なっています。つまり、これは商の導関数の公式が正しく機能していることを示唆しています。

合成関数の導関数の公式を確かめる

最後に、④合成関数の導関数の公式が正しく機能しているかを次の関数3を例にして考えていきます。

関数3

$$
y = (x^2-2x-1)^2
$$

アルゴリズム設計

こちらも、基本的には、積の導関数の公式を確かめたときと同じやり方になります。
① 導関数は前方差分で計算することにします。

② 関数3を次のように考えます。

$$
f(x) = x^2, \ \ \ \ g(x) = x^2-2x-1, \ \ \ \
h(x) = f(g(x)) = (x^2-2x-1)^2
$$

③ 関数$${f(x), g(x), h(x)}$$の導関数$${f'(x), g'(x), h'(x)}$$を前方差分を用いて求めます。

④ 最後に、これらの導関数を用いて、$${h'(x)}$$と$${f'(u)g'(x)}$$（ただし、$${u = g(x)}$$）のグラフを描きます。これらのグラフが一致すれば、合成関数の導関数の公式が正しく機能していると考えることができます。

プログラム

それでは、合成関数の導関数の公式が正しく機能しているかを確認するためのプログラムを作成していきます。

今度もスケッチ「check_product_formula」を再利用して作成していきます。
スケッチ「check_product_formula」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「check_composite_formula」と変更し、またスケッチ「check_composite_formula」内の「check_product_formula.pde」ファイルの名前を「check_composite_formula.pde」に変更します。そして、pdeファイル「check_composite_formula.pde」をダブルクリックしてスケッチ「check_composite_formula」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「check_composite_formula」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。

float x_range = 5.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 5.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500);
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  noFill();
  
  // グラフの描画範囲  
  float x_min = -x_range;
  float x_max = x_range;
  
  // 導関数 dh のグラフを描く
  stroke(0,255,0);  
  strokeWeight(5);
  draw_dh(x_min, x_max);

  // 合成関数の導関数 df(u) dg(x) のグラフを描く
  stroke(255,0,0);
  strokeWeight(2);
  draw_composite_formula(x_min, x_max);

}

// 関数 f(x)
float f(
  float x
){
  return x*x;
}

// 関数 g(x)
float g(
  float x
){
  return x*x-2.0*x-1.0;
}

// 関数 h(x)
float h(
  float x
){
  return f(g(x));
}

// 関数 f(x) の導関数
float df(
  float x
){
  float dx = 0.001;
  return (f(x+dx)-f(x))/dx;
}

// 関数 g(x) の導関数
float dg(
  float x
){
  float dx = 0.001;
  return (g(x+dx)-g(x))/dx;
}

// 関数 h(x) の導関数
float dh(
  float x
){
  float dx = 0.001;
  return (h(x+dx)-h(x))/dx;
}

// 導関数 dh を描く関数
void draw_dh(
  float x_min, // グラフの定義域の下限
  float x_max  // グラフの定義域の上限
){
  int plot_num = 2000; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=1; i<plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // 曲線上の点のx座標
    y = dh(x); // 曲線上の点のyの値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

}

// 合成関数の導関数 df(u) dg(x) を描く関数
void draw_composite_formula(
  float x_min, // グラフの定義域の下限
  float x_max  // グラフの定義域の上限
){
  int plot_num = 2000; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float u; // 補助変数 u=g(x)
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=1; i<plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // 曲線上の点のx座標
    u = g(x);
    y = df(u)*dg(x); // 曲線上の点のyの値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

}

ソースコード3　合成関数の導関数の公式が正しく機能しているかを確認するためのプログラム

ソースコード3とソースコード1との違いは、関数 f と g とを問題3に合わせて書き換えた部分と、商の導関数 df(u) dg(x) のグラフを描くための関数を draw_composite_formula 関数として準備したところになります。

ソースコード3を、スケッチ「check_composite_formula」の「check_composite_formula」タブのテキストエディタ部分に書いて実行すると、図3のように、実行ウィンドウのキャンバス上に導関数$${h'(x)}$$のグラフが緑色の太線で、合成関数の導関数$${f'(u)g'(x)}$$（ただし、$${u = g(x)}$$）のグラフが赤色の線でそれぞれ描かれます。

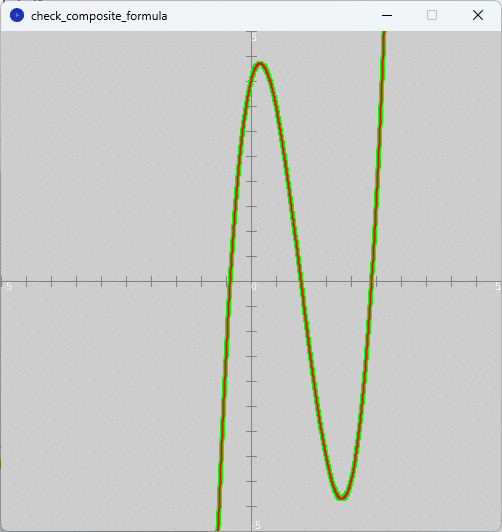
図3を見ると、導関数$${h'(x)}$$のグラフと合成関数の導関数$${f'(u)g'(x)}$$（ただし、$${u = g(x)}$$）のグラフとが重なっています。つまり、これは合成関数の導関数の公式が正しく機能していることを示唆しています。

まとめ

今回は、数学IIIで学ぶ「微分係数と導関数」について、導関数の公式が正しく機能することを確認するためのプログラムを作成しました。
特に、関数の積の導関数の公式、商の導関数の公式、および合成関数の導関数の公式について、具体的な関数を例に正しく機能することを確認しました。もちろん、これらの公式は導関数の定義から導くことができますが、今回のようにプログラムを用いて確かめることも勉強になると思います。残りの導関数の公式も同様にして正しく機能しているか、プログラムを用いて確認できます。演習問題としたので、是非チャレンジしてみてください。

読んだ感想などをお寄せください

本記事を読んだ感想や質問などを以下のお問い合せフォームからお寄せください。感想、質問をいただいた方には本記事の演習問題の解答をプレゼントします。（お問合せフォームの本文に、本記事のタイトルを入れてください。）

参考文献

改訂版教科書傍用スタンダード・オリジナル数学III（数研出版、ISBN9784410209567）

演習問題

次の関数を利用して、⑤逆関数の導関数の公式と⑥$${x^p}$$の導関数の公式とが正しく機能しているかを確かめるプログラムを作成してください。

$$
y=f(x)=\sqrt[3]{x} \ \ (x \geq 0)
$$

演習問題の解答例

ここから先は

839字 / 2画像 / 2ファイル

ログイン

この記事が気に入ったらチップで応援してみませんか？