
高校数学をプログラミングで解く(数学III編)「6-5 関数のグラフ」
マガジンリスト > 数学Ⅲ編 6.微分法の応用 > 6-5 関数のグラフ
はじめに
今回は、数学IIIで学ぶ「関数のグラフ」について、第2次導関数を用いて任意の関数$${f(x)}$$の極値と変曲点を求めて、その関数のグラフに極値と変曲点を取る点をプロットするプログラムを作成していきます。
関数のグラフ
まず、関数のグラフについて解説しておきます。
曲線の凹凸
関数$${f(x)}$$は第2次導関数$${f''(x)}$$をもつとする。
曲線$${y=f(x)}$$は
$${f''(x) > 0}$$である区間では 下に凸
$${f''(x) < 0}$$である区間では 上に凸
変曲点
関数$${f(x)}$$は第2次導関数$${f''(x)}$$をもつとする。
① $${f''(a)=0}$$のとき、$${x=a}$$の前後で$${f''(x)}$$の符号が変わるならば、点$${(a,f(a))}$$は曲線$${y=f(x)}$$の変曲点である。
② 点$${(a,f(a))}$$が曲線$${y=f(x)}$$の変曲点ならば $${f''(a)=0}$$
注意 $${f''(a)=0}$$であっても、点$${\mathrm{P}(a, f(a))}$$は変曲点であるとは限らない。例:$${y=x^4}$$における点$${(0,0)}$$
関数のグラフの描き方
$${y=f(x)}$$のグラフを描くときには、次のことを調べる。
① 定義域 $${(\mathrm{分母}) \neq 0}$$、$${(\mathrm{根号内}) \geq 0}$$、真数条件などに注意
② 増減、極値 $${y'}$$の符号の変化を調べる
③ 凹凸、変曲点 $${y''}$$の符号の変化を調べる
$${\rightarrow}$$ ②③で増減表をかく
④ 漸近線
$${x \to \infty}$$、$${x \to -\infty}$$のときを考える。
特に、分数関数では、分母が$${0}$$になる$${x}$$の値に着目する。
⑤ 対称性
$${f(-x)=f(x)}$$なら、$${y}$$軸に関して対称
$${f(-x)=-f(x)}$$なら、原点に関して対称
⑥ 座標軸との共有点など、簡単にわかる曲線上の点
漸近線の求め方
関数$${y=f(x)}$$のグラフについて
① $${y}$$軸に垂直な漸近線
$$
\lim_{x \to \pm \infty} f(x) = a \ \ \ \ \Leftrightarrow \ \ \ \ \mathrm{直線} y=a \mathrm{が漸近線}
$$
② $${x}$$軸に垂直な漸近線
$$
\lim_{x \to b \pm 0} f(x) = \pm \infty \ \ \ \ \Leftrightarrow \ \ \ \ \mathrm{直線} x=b \mathrm{が漸近線}
$$
③ $${x}$$軸に垂直でない漸近線
$$
\lim_{x \to \pm \infty} \{ f(x) - (ax+b) \} = 0 \ \ \ \ \Leftrightarrow \ \ \ \ \mathrm{直線} y=ax+b \mathrm{が漸近線}
$$
注意
$$
\lim_{x \to \pm \infty} \frac{f(x)}{x} = a, \ \ \lim_{x \to \pm \infty} (f(x) - ax) = b \ \ \ \ \Leftrightarrow \ \ \ \ \mathrm{直線} y=ax+b \mathrm{が漸近線}
$$
第2次導関数と極値
$${x=a}$$を含むある区間で$${f''(x)}$$は連続であるとする。
①$${f'(a)=0}$$かつ$${f''(a) < 0}$$ならば $${f(a)}$$は極大値
②$${f'(a)=0}$$かつ$${f''(a) > 0}$$ならば $${f(a)}$$は極小値
注意 $${f'(a)=0}$$、$${f''(a)=0}$$のときは、$${f(a)}$$が極値である場合も、極値でない場合もある。
関数の極大・極小を計算する
記事『高校数学をプログラミングで解く(数学II編)「5-3 関数の値の変化」』では、3次関数に対して極大・極小を求めました。3次関数の場合、その導関数は2次関数となるので、極値を求める方程式$${f'(x)=0}$$は2次方程式となり、解と係数の関係を用いて極値の位置を求めることができました。
また、記事『高校数学をプログラミングで解く(数学III編)「6-3 関数の値の変化」』では、より一般的な関数に対して極大・極小を求めました。このときは、$${f'(a)=0}$$を満たす$${x=a}$$の前後で
$${f'(x)}$$の符号が正から負に変わるならば $${f(a)}$$は極大値
$${f'(x)}$$の符号が負から正に変わるならば $${f(a)}$$は極小値
という条件で極値が極大か極小かを判定しました。
今回も、一般的な関数に対して極大・極小を求めることを考えます。ただし、極大・極小の判定は上記第2次導関数と極値で解説した、第2次導関数を用いた方法を用います。
問題
次の関数の極値を求め、そのグラフを描き、極値をプロットせよ。
$$
y = -\frac{3x}{x^2+3}
$$
アルゴリズム設計
問題の導関数、第2次導関数はそれぞれ
$$
y' = f'(x) = \frac{3(x^2-3)}{(x^2+3)^2}, \ \ y'' = f''(x)= -\frac{6x(x^2-9)}{(x^2+3)^3}
$$
となります。今回はこれら導関数、第2次導関数を利用して、以下の手順で極値を求めていきます。
① $${x}$$をグラフの描画範囲内で小さい方から動かして、$${f'(x)=0}$$を満たしていれば、そのときの$${x}$$の値が極値を取る値となります。
② その$${x}$$の値の位置での第2次導関数の値$${f''(x)}$$を調べることで、極値が極大値なのか、極小値なのかを決定することができます。
プログラム
それでは、関数に対する極値を求め、その関数のグラフに極値を取る点をプロットするプログラムを作成します。
今回は、記事『高校数学をプログラミングで解く(数学III編)「6-3 関数の値の変化」』で作成したスケッチ「calcandplotExtrema2」を再利用して作成していきます。以下の zip ファイルをダウンロードして展開または解凍してください。
そして、スケッチの名前(フォルダ名)を「calcandplotExtrema3」と変更し、またスケッチ「calcandplotExtrema3」内の「calcandplotExtrema2.pde」ファイルの名前を「calcandplotExtrema3.pde」に変更します。そして、pdeファイル「calcandplotExtrema3.pde」をダブルクリックしてスケッチ「calcandplotExtrema3」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「calcandplotExtrema3」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 5.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500);
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill();
// 関数のグラフを描く
stroke(0,0,0);
float x_min = -x_range;
float x_max = x_range;
draw_function(x_min, x_max);
// 極値を計算してプロットする
calc_and_plot_extrema(x_min, x_max);
}
// 関数
float f(
float x
){
return -3.0*x/(x*x+3.0);
}
// 導関数
float f_prime(
float x
){
return 3.0*(x*x-3.0)/pow(x*x+3.0,2.0);
}
// 第2次導関数
float f_prime2(
float x
){
return -6.0*x*(x*x-9.0)/pow(x*x+3.0,3.0);
}
// 関数のグラフを描く関数
void draw_function(
float x_min, // グラフの定義域の下限
float x_max // グラフの定義域の上限
){
int plot_num = 2000; // グラフを描くための頂点の個数
// グラフを描画
float x, y; // 関数の座標
float X, Y; // キャンバス上の座標
beginShape();
for(int i=1; i<plot_num; i++){
x = x_min + (x_max - x_min) / plot_num * i; // 曲線上の点のx座標
y = f(x); // 曲線上の点のyの値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
}
// 極値を計算してプロットする関数
void calc_and_plot_extrema(
float x_min, // グラフの定義域の下限
float x_max // グラフの定義域の上限
){
// 極値を求めてプロットする
float epsilon = 0.0001;
float dx = 0.001;
int n = (int)((x_max-x_min)/dx);
float x, y;
// float before_f, after_f;
for(int i=1; i<n; i++){
x = x_min+i*dx;
if( abs(f_prime(x)) < epsilon ){
y = f(x);
if( f_prime2(x) < 0.0 ){
// 極大値であれば赤色でプロット
stroke(255,0,0);
println("極大値:", x, y);
} else if( f_prime2(x) > 0.0 ){
// 極小値であれば青色でプロット
stroke(0,0,255);
println("極小値:", x, y);
} else {
// 極値であるか不明であれば緑色でプロット
stroke(0,255,0);
println("極値であるか不明:", x, y);
}
plot_extrema_point(x);
}
}
}
// 極値をプロットする関数
void plot_extrema_point(
float x // 極値のx座標
){
float y = f(x);
float X, Y; // キャンバス上の座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
strokeWeight(5);
point(X, Y);
strokeWeight(1);
}ソースコード1 関数に対する極値を求め、その関数のグラフに極値を取る点をプロットするプログラム
記事『高校数学をプログラミングで解く(数学III編)「6-3 関数の値の変化」』で作成したスケッチ「calcandplotExtrema2」との違いは、第2次導関数として、f_prime2 関数を導入して極値が極大か極小かを判定するために利用していることです。また、もう一つ重要なポイントは、$${f'(x) = 0}$$を満たす$${x}$$の値で$${f''(x) < 0}$$でも$${f''(x) > 0}$$でもなく、$${f''(x) = 0}$$となった場合です。この場合、「極値ではない」ではなく「極値かどうかわからない」という判定になります。そのため、$${f''(x) = 0}$$のときは、点$${(x,f(x))}$$を関数のグラフ上に緑色の点で表すこととし、コンソールには「極値であるか不明」と出力するようにしました。
ソースコード1を、スケッチ「calcandplotExtrema3」の「calcandplotExtrema3」タブのテキストエディタ部分に書いて実行すると、図1のように、実行ウィンドウのキャンバス上に、問題の関数(黒色)とその関数の極大値(赤色)、極小値(青色)が描かれます。なお、今回の問題の関数では「極値であるか不明」となる点はありません。
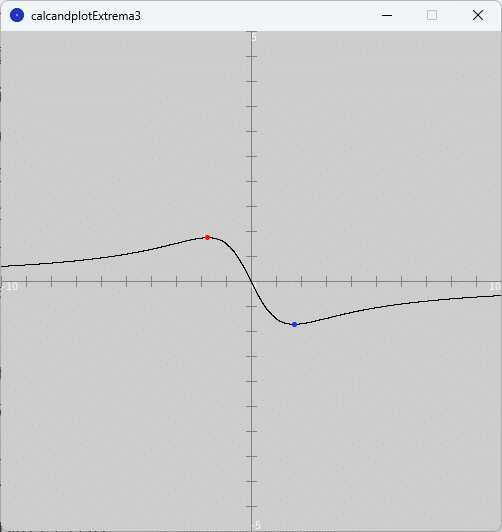
また、図2のように、開発環境ウィンドウのコンソールに、
極大値: -1.7319994 0.86602545
極小値: 1.7320004 -0.8660254
と、極大値、極小値の位置とその値が出力されます。

考察
問題の関数のグラフでは$${f'(x) = 0}$$を満たす$${x}$$の値で$${f''(x) = 0}$$となる点はありませんでしたので、ここでは、$${y=x^4}$$を例にして、$${f'(x) = 0}$$かつ$${f''(x) = 0}$$となる点について考えてみます。
$${y=x^4}$$の場合、導関数と第2次導関数はそれぞれ
$$
y'=f'(x)=4x^3, \ \ y''=f''(x)=12x^2
$$
となります。ソースコード1の関数 f 、f_prime、f_prime2 をこれらの関数に置き換え、極値を計算してプロットする関数 calc_and_plot_extrema 内の$${f'(x)=0}$$を判定するための変数 epsilon を 0.000000001 に設定して実行すると、図3のように、$${y=x^4}$$のグラフの$${x=0}$$の位置に緑色の点がプロットされます。

また、図4のように、開発環境ウィンドウのコンソールに
極値であるか不明: 0.0 0.0
と表示されます。

図3をみると、$${y=x^4}$$の$${x=0}$$での点は極小値になっていますが、図4のコンソールに出力された判定結果は「極値であるか不明」となっています。これは、ソースコード1で$${f'(x) = 0}$$を満たす$${x}$$の値で$${f''(x) = 0}$$となった場合「極値であるか不明」としているからです。4次関数の場合、$${f'(0)=0}$$、$${f''(0)=0}$$となりますので、「極値であるか不明」となるのは当然のこととなります。
しかし、これは第2次導関数で判定できないというだけで、他の方法であれば判定することができます。実際、記事『高校数学をプログラミングで解く(数学III編)「6-3 関数の値の変化」』で説明した $${f'(a)=0}$$を満たす$${x=a}$$の前後で$${f'(x)}$$の符号を見る方法 であれば判定することができます。ここでは、$${f'(x) = 0}$$を満たす$${x}$$の値で$${f''(x) = 0}$$となった場合にも極値の判定ができるようにソースコード1にそのコードを追加してみます。
float x_range = 2.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 2.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500);
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill();
// 関数のグラフを描く
stroke(0,0,0);
float x_min = -x_range;
float x_max = x_range;
draw_function(x_min, x_max);
// 極値を計算してプロットする
calc_and_plot_extrema(x_min, x_max);
}
// 関数
float f(
float x
){
return x*x*x*x;
}
// 導関数
float f_prime(
float x
){
return 4.0*x*x*x;
}
// 第2次導関数
float f_prime2(
float x
){
return 12.0*x*x;
}
// 関数のグラフを描く関数
void draw_function(
float x_min, // グラフの定義域の下限
float x_max // グラフの定義域の上限
){
int plot_num = 2000; // グラフを描くための頂点の個数
// グラフを描画
float x, y; // 関数の座標
float X, Y; // キャンバス上の座標
beginShape();
for(int i=1; i<plot_num; i++){
x = x_min + (x_max - x_min) / plot_num * i; // 曲線上の点のx座標
y = f(x); // 曲線上の点のyの値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
}
// 極値を計算してプロットする関数
void calc_and_plot_extrema(
float x_min, // グラフの定義域の下限
float x_max // グラフの定義域の上限
){
// 極値前後の小さな区間[x-e,x+e]
float e = 0.01;
// 極値を求めてプロットする
float epsilon = 0.000000001;
float dx = 0.001;
int n = (int)((x_max-x_min)/dx);
float x, y;
float before_f, after_f;
for(int i=1; i<n; i++){
x = x_min+i*dx;
if( abs(f_prime(x)) < epsilon ){
y = f(x);
if( f_prime2(x) < 0.0 ){
// 極大値であれば赤色でプロット
stroke(255,0,0);
println("極大値:", x, y);
} else if( f_prime2(x) > 0.0 ){
// 極小値であれば青色でプロット
stroke(0,0,255);
println("極小値:", x, y);
} else {
before_f = f_prime(x-e);
after_f = f_prime(x+e);
if( before_f > 0.0 && after_f < 0.0 ){
// 極大値であれば赤色でプロット
stroke(255,0,0);
println("極大値:", x, y);
} else if(before_f < 0.0 && after_f > 0.0 ){
// 極小値であれば青色でプロット
stroke(0,0,255);
println("極小値:", x, y);
} else {
// 極値でなければ緑色でプロット
stroke(0,255,0);
println("極値ではない:", x, y);
}
}
plot_extrema_point(x);
}
}
}
// 極値をプロットする関数
void plot_extrema_point(
float x // 極値のx座標
){
float y = f(x);
float X, Y; // キャンバス上の座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
strokeWeight(5);
point(X, Y);
strokeWeight(1);
}ソースコード2 ソースコード1に$${f'(x) = 0}$$、$${f''(x) = 0}$$となる点での極値判定を追加
スケッチ「calcandplotExtrema3」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「calcandplotExtrema4」と変更し、またスケッチ「calcandplotExtrema4」内の「calcandplotExtrema3.pde」ファイルの名前を「calcandplotExtrema4.pde」に変更します。そして、pdeファイル「calcandplotExtrema4.pde」をダブルクリックしてスケッチ「calcandplotExtrema4」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「calcandplotExtrema4」タブを選択し、そのテキストエリアのソースコードを上記ソースコード2で書き換えて実行すると、図5のように、実行ウィンドウのキャンバス上の4次関数の$${x=0}$$の位置に青色の点がプロットされ、今度は、正しく極小値であることが示されます。

また、図6のように、開発環境ウィンドウのコンソールに
極小値: 0.0 0.0
と表示されます。

関数の変曲点を求める
今度は、関数に対する極値だけでなく、関数の変曲点についても求めることを考えます。変曲点は上記変曲点①で解説したように第2次導関数を調べることで求めることができます。
プログラム
アルゴリズムは上記変曲点①で解説していることをそのまま実装するだけですので、早速、関数に対する極値と変曲点を求め、その関数のグラフに極値と変曲点を取る点をプロットするプログラムを作成します。
スケッチ「calcandplotExtrema4」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「calcandplotExtremaandinflection」と変更し、またスケッチ「calcandplotExtremaandinflection」内の「calcandplotExtrema4.pde」ファイルの名前を「calcandplotExtremaandinflection.pde」に変更します。そして、pdeファイル「calcandplotExtremaandinflection.pde」をダブルクリックしてスケッチ「calcandplotExtremaandinflection」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「calcandplotExtremaandinflection」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 5.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500);
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill();
// 関数のグラフを描く
stroke(0,0,0);
float x_min = -x_range;
float x_max = x_range;
draw_function(x_min, x_max);
// 極値を計算してプロットする
calc_and_plot_extrema_and_inflection(x_min, x_max);
}
// 関数
float f(
float x
){
return -3.0*x/(x*x+3.0);
}
// 導関数
float f_prime(
float x
){
return 3.0*(x*x-3.0)/pow(x*x+3.0,2.0);
}
// 第2次導関数
float f_prime2(
float x
){
return -6.0*x*(x*x-9.0)/pow(x*x+3.0,3.0);
}
// 関数のグラフを描く関数
void draw_function(
float x_min, // グラフの定義域の下限
float x_max // グラフの定義域の上限
){
int plot_num = 2000; // グラフを描くための頂点の個数
// グラフを描画
float x, y; // 関数の座標
float X, Y; // キャンバス上の座標
beginShape();
for(int i=1; i<plot_num; i++){
x = x_min + (x_max - x_min) / plot_num * i; // 曲線上の点のx座標
y = f(x); // 曲線上の点のyの値
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
}
// 極値と変曲点を計算してプロットする関数
void calc_and_plot_extrema_and_inflection(
float x_min, // グラフの定義域の下限
float x_max // グラフの定義域の上限
){
// 極値前後の小さな区間[x-e,x+e]
float e = 0.01;
// 極値と変曲点を求めてプロットする
float epsilon = 0.00005;
float dx = 0.001;
int n = (int)((x_max-x_min)/dx);
float x, y;
float before_f, after_f;
for(int i=1; i<n; i++){
x = x_min+i*dx;
// 極値を求める
if( abs(f_prime(x)) < epsilon ){
y = f(x);
if( f_prime2(x) < 0.0 ){
// 極大値であれば赤色でプロット
stroke(255,0,0);
println("極大値:", x, y);
} else if( f_prime2(x) > 0.0 ){
// 極小値であれば青色でプロット
stroke(0,0,255);
println("極小値:", x, y);
} else {
before_f = f_prime(x-e);
after_f = f_prime(x+e);
if( before_f > 0.0 && after_f < 0.0 ){
// 極大値であれば赤色でプロット
stroke(255,0,0);
println("極大値:", x, y);
} else if(before_f < 0.0 && after_f > 0.0 ){
// 極小値であれば青色でプロット
stroke(0,0,255);
println("極小値:", x, y);
} else {
// 極値でなければ緑色でプロット
stroke(0,255,0);
println("極値ではない:", x, y);
}
}
plot_extrema_point(x);
}
// 変曲点を求める
if( abs(f_prime2(x)) < epsilon ){
y = f(x);
before_f = f_prime2(x-e);
after_f = f_prime2(x+e);
if( before_f * after_f < 0.0 ){
// 変曲点であれば赤色でプロット
stroke(255,255,0);
println("変曲点:", x, y);
}
plot_extrema_point(x);
}
}
}
// 極値をプロットする関数
void plot_extrema_point(
float x // 極値のx座標
){
float y = f(x);
float X, Y; // キャンバス上の座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
strokeWeight(5);
point(X, Y);
strokeWeight(1);
}ソースコード3 関数に対する極値と変曲点を求め、その関数のグラフに極値と変曲点を取る点をプロットするプログラム
なお、ソースコード3に加えた変曲点を求める部分で、変曲点かどうかを判定する方法として、$${f''(x)=0}$$となる$${x}$$の前後の位置での値$${f''(x+e)}$$と$${f''(x-e)}$$との積が負の値になるかどうかで判定しています。「$${f''(x+e) > 0}$$かつ$${f''(x-e) < 0}$$」または 「$${f''(x+e) < 0}$$かつ$${f''(x-e) > 0}$$」を調べて判定することもできますが、コードが少し煩雑になりますので、やはり積を調べた方がシンプルでいいと思います。
ソースコード3を、スケッチ「calcandplotExtremaandinflection」の「calcandplotExtremaandinflection」タブのテキストエディタ部分に書いて実行すると、図7のように、実行ウィンドウのキャンバス上に、問題の関数(黒色)とその関数の極大値(赤色)、極小値(青色)に加えて3つの変曲点(黄色)が描かれます。

また、図8のように、開発環境ウィンドウのコンソールに
変曲点: -2.9999995 0.75
極大値: -1.7319994 0.86602545
変曲点: 0.0 -0.0
極小値: 1.7320004 -0.8660254
変曲点: 3.000001 -0.7499999
と表示されます。

これらの結果が正しいことは、問題の関数の増減表などを作成して、確かめておいてください。
まとめ
今回は、数学IIIで学ぶ「関数のグラフ」について、第2次導関数を用いて任意の関数$${f(x)}$$の極値と変曲点を求めて、その関数のグラフに極値と変曲点を取る点をプロットするプログラムを作成しました。
関数の極大・極小を判定する方法として今回第2次導関数を用いて行いました。記事『高校数学をプログラミングで解く(数学III編)「6-3 関数の値の変化」』で関数の極大・極小を考えたときは、$${f'(a)=0}$$を満たす$${x=a}$$の前後で$${f'(x)}$$の符号がどのように変化するかで極大か極小かを判断していましたが、第2次導関数を用いた方法であればもう少しシンプルに判定できることがわかりました。ただ、$${f'(a) = 0}$$、$${f''(a) = 0}$$となる点での極値判定を第2次導関数だけではできませんので、この場合は$${x=a}$$の前後で$${f'(x)}$$の符号がどのように変化するかを見る必要があります。ですので、両方の方法をきちんと使えるようにしておきましょう。
読んだ感想などをお寄せください
本記事を読んだ感想や質問などを以下のお問い合せフォームからお寄せください。感想、質問をいただいた方には本記事の演習問題の解答をプレゼントします。(お問合せフォームの本文に、本記事のタイトルを入れてください。)
参考文献
改訂版 教科書傍用 スタンダード・オリジナル 数学III(数研出版、ISBN9784410209567)
演習問題
次の関数の極値や変曲点を求め、そのグラフを描き、極値と変曲点をプロットするプログラムを作成してください。
$$
y = \frac{\log x}{x^2+1}
$$
演習問題の解答例
ここから先は
この記事が気に入ったらチップで応援してみませんか?
