高校数学をプログラミングで解く（数学B編）「2-2 空間ベクトルと成分」

2024年6月8日 08:00

マガジンリスト　＞　数学B編 2.空間のベクトル　＞　2-2 空間ベクトルと成分

はじめに

今回は、数学Bで学ぶ「空間ベクトルと成分」について、空間ベクトルの基本的な演算を Processing でどのように扱うのかを解説し、実際にそれらの演算を行い、空間ベクトルを表示するプログラムを作成します。

ベクトルの演算

まず、空間ベクトルの基本的な演算についてまとめておきます。記事『高校数学をプログラミングで解く（数学B編）「1-1 ベクトルの演算」』でまとめた平面のベクトルの場合と同様に定義できます。
なお、以下で$${k, l}$$は実数とし、$${\vec{a} = (a_1, a_2, a_3), \ \vec{b} = (b_1, b_2, b_3)}$$とします。

空間ベクトルの相等

$$
\begin{array}{rcl}
\vec{a} = \vec{b} & \Leftrightarrow & \vec{a} \mathrm{と} \vec{b} \mathrm{の向きが同じで大きさが等しい} \\
& \Leftrightarrow & (a_1, a_2, a_3) = (b_1, b_2, b_3) \\
& \Leftrightarrow & a_1 = b_1, a_2 = b_2, a_3 = b_3
\end{array}
$$

空間ベクトルの和

$$
\vec{a} + \vec{b} = (a_1, a_2, a_3) + (b_1, b_2, b_3) = (a_1+b_1, a_2+b_2, a_3+b_3)
$$

空間ベクトルの差

$$
\vec{a} - \vec{b} = (a_1, a_2, a_3) - (b_1, b_2, b_3) = (a_1-b_1, a_2-b_2, a_3-b_3)
$$

空間ベクトルの大きさ

$$
|\vec{a}| = \sqrt{a_1^2+a_2^2+a_3^2}
$$

空間ベクトルの実数倍

$$
k \vec{a} = ( ka_1, ka_2, ka_3)
$$

演算法則

$$
\vec{a} + \vec{b} = \vec{b} + \vec{a} = (a_1+b_1, a_2+b_2, a_3+b_3) = (b_1+a_1, b_2+a_2, b_3+a_3) \\
(\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c}) \\
k(l \vec{a}) = (kl) \vec{a} = k(la_1, la_2, la_3) = (kla_1, kla_2, kla_3) \\
(k+l) \vec{a} = k \vec{a} + l \vec{a} \\
= (ka_1, ka_2, ka_3) + (la_1, la_2, la_3) = ((k+l)a_1, (k+l)a_2, (k+l)a_3) \\
k(\vec{a}+\vec{b}) = k\vec{a} + k \vec{b} = (k(a_1+b_1), k(a_2+b_2), k(a_3+b_3))
$$

空間ベクトルの平行条件

$${ \vec{a} \neq \vec{0}, \vec{b} \neq \vec{0} }$$のとき、

$$
\vec{a} /\!\!/ \vec{b} \ \ \ \ \Leftrightarrow \ \ \ \ \vec{b}=k \vec{a} \mathrm{となる実数}k\mathrm{がある}
$$

空間ベクトルの分解

4点$${\mathrm{O, A, B, C}}$$は同じ平面上にないとする。
$${\overrightarrow{\mathrm{OA}}=\vec{a}, \overrightarrow{\mathrm{OB}}=\vec{b}, \overrightarrow{\mathrm{OC}}=\vec{c} }$$とすると、任意のベクトル$${\vec{p}}$$は、

$$
\vec{p} = s \vec{a} + t \vec{b} + u \vec{c}
$$

（$${s, t, u}$$は実数）の形にただ１通りに表される。

座標と空間ベクトル

$${\mathrm{A}(a_1, a_2, a_3), \mathrm{B}(b_1, b_2, b_3)}$$とする。

$$
\overrightarrow{\mathrm{AB}} = (b_1-a_1, b_2-a_2, b_3-a_3), \\ | \overrightarrow{\mathrm{AB}}| = \sqrt{ (b_1-a_1)^2+(b_2-a_2)^2+(b_3-a_3)^2}
$$

Processingで空間ベクトルを扱う

記事『高校数学をプログラミングで解く（数学B編）「1-1 ベクトルの演算」』で、プログラミング言語 Processing ではベクトルを扱うための PVector クラスというものが用意されていることを説明しました。実は、空間ベクトルも同じ PVector クラスで扱うことができます。PVector クラスを用いて空間ベクトル演算を行う方法もベクトルの成分が２つから３つに変わっただけで記事『高校数学をプログラミングで解く（数学B編）「1-1 ベクトルの演算」』にまとめたものと同じですが、念のため、説明しておきます。

ベクトルの生成

まず、プログラムで利用するベクトルの生成について解説します。以下のソースコードで変数 a をベクトル$${\vec{a}}$$のように扱うことができます。

PVector a = new PVector(a1,a2,a3);

各引数は次のようになっています。

a1：ベクトルの$${x}$$成分　float型
a2：ベクトルの$${y}$$成分　float型
a3：ベクトルの$${z}$$成分　float型

ベクトルの和

次に、ベクトルの和について解説します。２つのベクトルの和は単純に”＋”の記号を利用して和を取れるわけではないことに注意してください。２つのベクトルの和を取るためには add 関数を利用します。

PVector a = new PVector(a1,a2,a3);
PVector b = new PVector(b1,b2,b3);
b.add(a);

これでベクトルの和は計算できるわけですが、１点注意が必要です。それは、「b.add(a);」と書いた場合、「変数 b のベクトルに変数 a のベクトルを加えて、変数 b に代入する」ということになります。つまり、変数 b のベクトルの値は変更されるわけです。
そこで、$${\vec{b}}$$の値は変更せずに、$${\vec{c} = \vec{b}+\vec{a}}$$を計算したい場合は以下のように書きます。

PVector a = new PVector(a1,a2,a3);
PVector b = new PVector(b1,b2,b3);
PVector c = b.copy().add(a); // b+aをcに代入、bは変更なし

つまり、変数 b に入っているベクトルをコピーして、そのコピーに変数 a に入っているベクトルを加え、そのベクトルを変数 c に代入するようにします。

ベクトルの差

ベクトルの差について解説します。ベクトルの和と同様に、２つのベクトルの差は単純に”－”の記号を利用して差を取れるわけではないです。２つのベクトルの差を取るためには sub 関数を利用します。

PVector a = new PVector(a1,a2,a3);
PVector b = new PVector(b1,b2,b3);
PVector c = b.copy().sub(a); // b-aをcに代入、bは変更なし
b.sub(a); // bをb-aに変更

ベクトルの大きさ

ベクトルの大きさについて解説します。ベクトルの大きさは定義通りにベクトルの成分を用いて計算することもできますが、PVector クラスでは mag 関数を利用して大きさを求めることができます。

PVector a = new PVector(a1,a2,a3);
float r = a.mag(); // ベクトルaの大きさ

なお、mag 関数は引数を取らず、ベクトルの大きさをfloat型の値で返します。

ベクトルの実数倍

ベクトルの実数倍について解説します。ベクトルの実数倍は mult 関数を利用します。

float k = 2.0;
PVector a = new PVector(a1,a2,a3);
PVector b = a.copy().mult(k); // ベクトルaをk倍してbに代入
a.mult(k); // ベクトルaをk倍する

各引数は次のようになっています。

k：ベクトルを k 倍にする　float型

ベクトル演算の例1

では、上記で説明した PVector クラスを用いて、実際に空間ベクトルを扱うプログラムを作成してみます。

問題1
$${\vec{a} = (1,-1,2), \vec{b}=(0,2,1)}$$のとき、次のベクトルを成分で表せ。
(1) $${ 3 \vec{a} }$$
(2) $${ \vec{a} + \vec{b} }$$
(3) $${ 2 \vec{a} + 3 \vec{b} }$$
(4) $${ 3 \vec{a} - 2 \vec{b} }$$

空間ベクトル演算のプログラム１

問題1を、ベクトルの成分を表すとともに、空間ベクトルとして図示するプログラムを作成します。
記事『高校数学をプログラミングで解く（数学B編）「2-0-3 右手系で図形を描く」』で作成したスケッチ「draw3DCoordinates_temp」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「operate3DVectors」と変更し、またスケッチ「operate3DVectors」内の「draw3DCoordinates_temp.pde」ファイルの名前を「operate3DVectors.pde」に変更します。そして、pdeファイル「operate3DVectors.pde」をダブルクリックしてスケッチ「operate3DVectors」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「operate3DVectors」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。

float range; // 座標系での表示範囲-range≦x,y.z≦range
float res; // 座標系のサイズをキャンバスのサイズに変換するパラメータ
float angle = 0.0;

PVector a, b; // 与えられた空間ベクトル
PVector c1, c2, c3, c4; // 演算後の空間ベクトル

void setup(){
  size(400, 400, P3D);
  noFill();
  ortho();
  range = 10.0; 
  res = width / 2.0 / range;

  // 2つの空間ベクトル
  a = new PVector(1.0, -1.0, 2.0);
  b = new PVector(0.0, 2.0, 1.0);
  
  // (1) 3a
  c1 = a.copy().mult(3.0);
  // (2) a+b
  c2 = a.copy().add(b.copy());
  // (3) 2a + 3b
  c3 = a.copy().mult(2.0).add(b.copy().mult(3.0));
  // (4) 3a - 2b
  c4 = a.copy().mult(3.0).sub(b.copy().mult(2.0));
  
  println("(1) 3a:", c1);
  println("(2) a+b:", c2);
  println("(3) 2a+3b:", c3);
  println("(4) 3a-2b:", c4);

}

void draw(){
  background(204); // 背景をグレーにする
  // 視点を設定する
  camera(200.0, -200.0, 100.0, 0.0, 0.0, 0.0, 0.0, 0.0, -1.0);
  // マウスボタンが押されたときの処理
  if(mousePressed){ 
    if( mouseButton == LEFT ){ // 左ボタンがおされたときはz軸時計周りに回転
      angle = angle + 1.0;
    } else if( mouseButton == RIGHT ){ // 右ボタンがおされたときはz軸反時計周りに回転
      angle = angle -1.0;
    } else {
    }
  }
  // z軸周りに回転
  rotateZ(radians(angle));

  // 座標軸の設定
  strokeWeight(1);
  fill(255,0,0);
  stroke(255,0,0);
  arrow3D(0.0,0.0,0.0,range * res,0.0,0.0); // x軸（赤色）
  fill(0,255,0);
  stroke(0,255,0);
  arrow3D(0.0,0.0,0.0,0.0,range * res,0.0); // y軸（緑色）
  fill(0,0,255);
  stroke(0,0,255);
  arrow3D(0.0,0.0,0.0,0.0,0.0,range * res); // z軸（青色）

  noFill();
  stroke(0,0,0);
  // 以下に、図形を描いていく
  
  // 空間ベクトルa, bを描く
  fill(0,0,0);
  stroke(0,0,0);
  arrow3D(0.0,0.0,0.0, a.x*res,a.y*res,a.z*res);
  fill(0,0,0);
  stroke(0,0,0);
  arrow3D(0.0,0.0,0.0, b.x*res,b.y*res,b.z*res);

  // (1) 3a（黄色）
  fill(255,255,0);
  stroke(255,255,0);
  arrow3D(0.0,0.0,0.0, c1.x*res,c1.y*res,c1.z*res);

  // (2) a+b（桃色）
  fill(255,0,255);
  stroke(255,0,255);
  arrow3D(0.0,0.0,0.0, c2.x*res,c2.y*res,c2.z*res);

  // (3) 2a+3b（水色）
  fill(0,255,255);
  stroke(0,255,255);
  arrow3D(0.0,0.0,0.0, c3.x*res,c3.y*res,c3.z*res);

  // (4) 3a-2b（白色）
  fill(255,255,255);
  stroke(255,255,255);
  arrow3D(0.0,0.0,0.0, c4.x*res,c4.y*res,c4.z*res);

}

ソースコード1　空間ベクトルの演算を行うプログラム

ソースコード1では、setup 関数内でベクトルの演算を行ってその結果をコンソールに出力することを行っており、繰り返し実行を行う draw 関数内でベクトルを図示するようにしています。これにより、図示したベクトルは角度を変えてみることができるようになります。

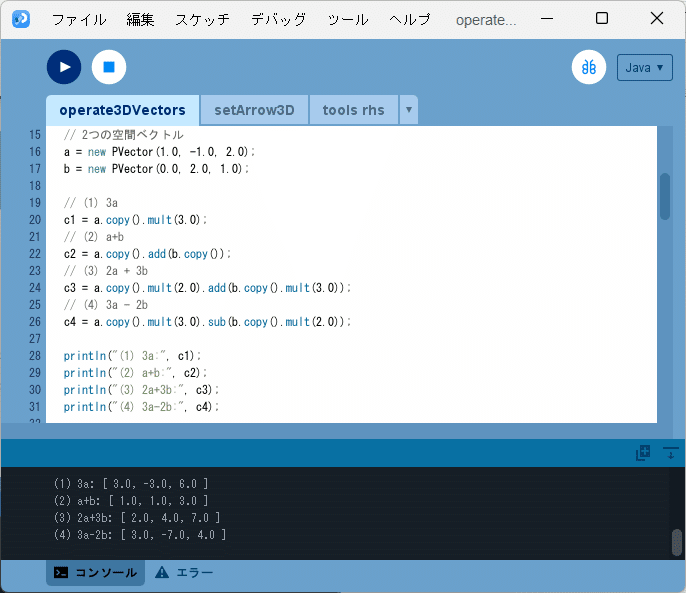
このスケッチ「operate3DVectors」を実行すると、図1のように、開発環境ウィンドウのコンソールの部分に、
(1) 3a: [ 3.0, -3.0, 6.0 ]
(2) a+b: [ 1.0, 1.0, 3.0 ]
(3) 2a+3b: [ 2.0, 4.0, 7.0 ]
(4) 3a-2b: [ 3.0, -7.0, 4.0 ]
と表示されます。

また、図2のように、実行ウィンドウのキャンバスに空間の座標系を表す３つの空間ベクトル（赤色：$${x}$$軸、緑色：$${y}$$軸、青色：$${z}$$軸）を基準にして、元の空間ベクトル$${\vec{a}}$$と$${\vec{b}}$$が黒色で、演算した結果の4つの空間ベクトルが順に黄色、桃色、水色、白色で表示されています。

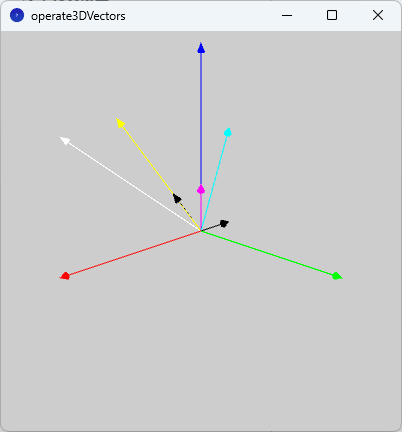
なお、実行ウィンドウのキャンバス内をクリックすると$${z}$$軸回りに図形が回転するので、いろいろな角度から空間ベクトルを眺めてみてください。

ベクトル演算の例2

次は、空間上のある点からもう一つの点に向かう空間ベクトルを扱うプログラムを作成してみます。

問題2
$${\mathrm{A}(0,1,2), \mathrm{B}(1,-1,1), \mathrm{C}(2,1,-1)}$$のとき、次のベクトルを成分で表せ。また、その大きさを求めよ。

空間ベクトル演算のプログラム2

記事『高校数学をプログラミングで解く（数学B編）「2-0-3 右手系で図形を描く」』で作成したスケッチ「draw3DCoordinates_temp」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「operate3DVectors2」と変更し、またスケッチ「operate3DVectors2」内の「draw3DCoordinates_temp.pde」ファイルの名前を「operate3DVectors2.pde」に変更します。そして、pdeファイル「operate3DVectors2.pde」をダブルクリックしてスケッチ「operate3DVectors2」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「operate3DVectors2」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。

float range; // 座標系での表示範囲-range≦x,y.z≦range
float res; // 座標系のサイズをキャンバスのサイズに変換するパラメータ
float angle = 0.0;

PVector a, b, c; // 与えられた空間上の点A,B,Cを表す座標
PVector d1, d2, d3, d4; // 演算後の空間ベクトル

void setup(){
  size(400, 400, P3D);
  noFill();
  ortho();
  range = 10.0; 
  res = width / 2.0 / range;

  // 3つの点を表す空間の座標
  a = new PVector(0.0, 1.0, 2.0);
  b = new PVector(1.0, -1.0, 1.0);
  c = new PVector(2.0, 1.0, -1.0);
  
  // (1) ベクトルAB
  d1 = b.copy().sub(a.copy());
  // (2) ベクトルBC
  d2 = c.copy().sub(b.copy());
  // (3) ベクトルAC
  d3 = c.copy().sub(a.copy());
  // (4) ベクトルCA
  d4 = a.copy().sub(c.copy());
  
  println("(1) ベクトルAB:", d1, " ABの大きさ:", d1.mag());
  println("(2) ベクトルBC:", d2, " BCの大きさ:", d2.mag());
  println("(3) ベクトルAC:", d3, " ACの大きさ:", d3.mag());
  println("(4) ベクトルCA:", d4, " CAの大きさ:", d4.mag());

}

void draw(){
  background(204); // 背景をグレーにする
  // 視点を設定する
  camera(200.0, -200.0, 100.0, 0.0, 0.0, 0.0, 0.0, 0.0, -1.0);
  // マウスボタンが押されたときの処理
  if(mousePressed){ 
    if( mouseButton == LEFT ){ // 左ボタンがおされたときはz軸時計周りに回転
      angle = angle + 1.0;
    } else if( mouseButton == RIGHT ){ // 右ボタンがおされたときはz軸反時計周りに回転
      angle = angle -1.0;
    } else {
    }
  }
  // z軸周りに回転
  rotateZ(radians(angle));

  // 座標軸の設定
  strokeWeight(1);
  fill(255,0,0);
  stroke(255,0,0);
  arrow3D(0.0,0.0,0.0,range * res,0.0,0.0); // x軸（赤色）
  fill(0,255,0);
  stroke(0,255,0);
  arrow3D(0.0,0.0,0.0,0.0,range * res,0.0); // y軸（緑色）
  fill(0,0,255);
  stroke(0,0,255);
  arrow3D(0.0,0.0,0.0,0.0,0.0,range * res); // z軸（青色）

  noFill();
  stroke(0,0,0);
  // 以下に、図形を描いていく
  
  // 空間上の3点A,B,Cを描く
  strokeWeight(5);
  fill(0,0,0);
  stroke(0,0,0);
  point_rhs(a.copy().mult(res));
  point_rhs(b.copy().mult(res));
  point_rhs(c.copy().mult(res));

  // (1) ベクトルAB（黄色）
  strokeWeight(1);
  fill(255,255,0);
  stroke(255,255,0);
  arrow3D(a.x*res,a.y*res,a.z*res, b.x*res,b.y*res,b.z*res);

  // (2) ベクトルBC（桃色）
  fill(255,0,255);
  stroke(255,0,255);
  arrow3D(b.x*res,b.y*res,b.z*res, c.x*res,c.y*res,c.z*res);

  // (3) ベクトルAC（水色）
  fill(0,255,255);
  stroke(0,255,255);
  arrow3D(a.x*res,a.y*res,a.z*res, c.x*res,c.y*res,c.z*res);

  // (4) ベクトルCA（白色）
  fill(255,255,255);
  stroke(255,255,255);
  arrow3D(c.x*res,c.y*res,c.z*res, a.x*res,a.y*res,a.z*res);

}

ソースコード2　空間ベクトルの演算を行うプログラム2

ソースコード2では、draw 関数内で「tools_rhs.pde」で定義した point_rhs 関数を利用して3点$${\mathrm{A, B, C}}$$をキャンバス内で描くようにしています。

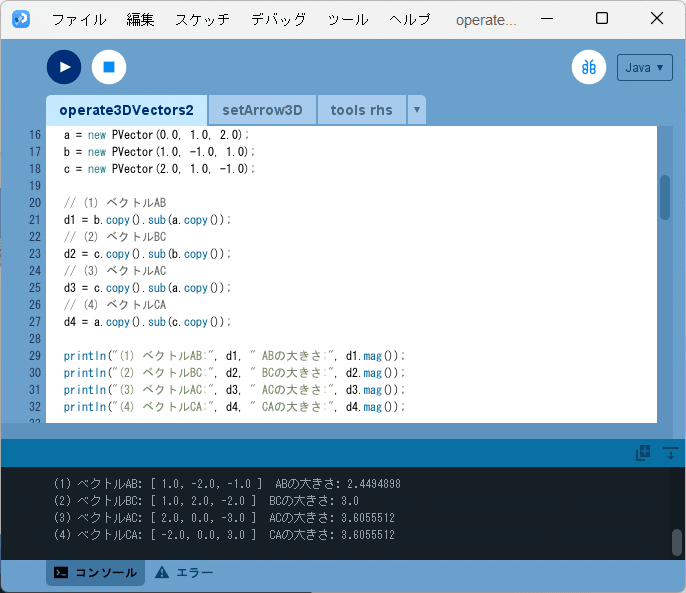
このスケッチ「operate3DVectors2」を実行すると、図3のように、開発環境ウィンドウのコンソールの部分に、

(1) ベクトルAB: [ 1.0, -2.0, -1.0 ] ABの大きさ: 2.4494898
(2) ベクトルBC: [ 1.0, 2.0, -2.0 ] BCの大きさ: 3.0
(3) ベクトルAC: [ 2.0, 0.0, -3.0 ] ACの大きさ: 3.6055512
(4) ベクトルCA: [ -2.0, 0.0, 3.0 ] CAの大きさ: 3.6055512

と表示されます。$${ \sqrt{6}=2.44948974\cdots, \sqrt{13}=3.60555127\cdots}$$ですので、正しい結果が得られていることがわかります。

また、図4のように、実行ウィンドウのキャンバスに3つの空間の座標$${\mathrm{A,B,C}}$$が黒色の点で描画され、演算した結果の4つの空間ベクトル$${\overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{AC}}, \overrightarrow{\mathrm{CA}} }$$が順に黄色、桃色、水色、白色で表示されています。

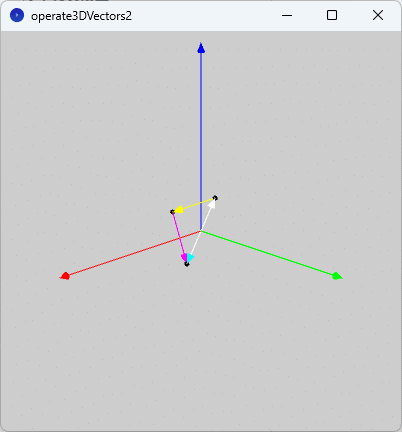
$${\overrightarrow{\mathrm{AC}}}$$（水色）と$${\overrightarrow{\mathrm{CA}} }$$（白色）は向きが反対で大きさが同じベクトルとなるので、重なって表示されています。水色のベクトルを描画した後、白色のベクトルを描画するので、矢印のシャフト部分が白色となっています。

まとめ

今回は、数学Bで学ぶ「空間ベクトルと成分」について、空間ベクトルの基本的な演算を Processing でどのように扱うのかを解説し、実際にそれらの演算を行い、空間ベクトルを表示するプログラムを作成しました。
空間ベクトルは、記事『高校数学をプログラミングで解く（数学B編）「1-1 ベクトルの演算」』で解説した平面ベクトルと同じように扱うことができ、プログラムでも平面ベクトルと同じ PVector クラスを用いて演算することができます。様々な空間ベクトルの演算や空間ベクトルの図示を行って少しずつベクトル演算のプログラミングに慣れていってください。

参考文献

改訂版教科書傍用スタンダード数学B（数研出版、ISBN9784410209468）