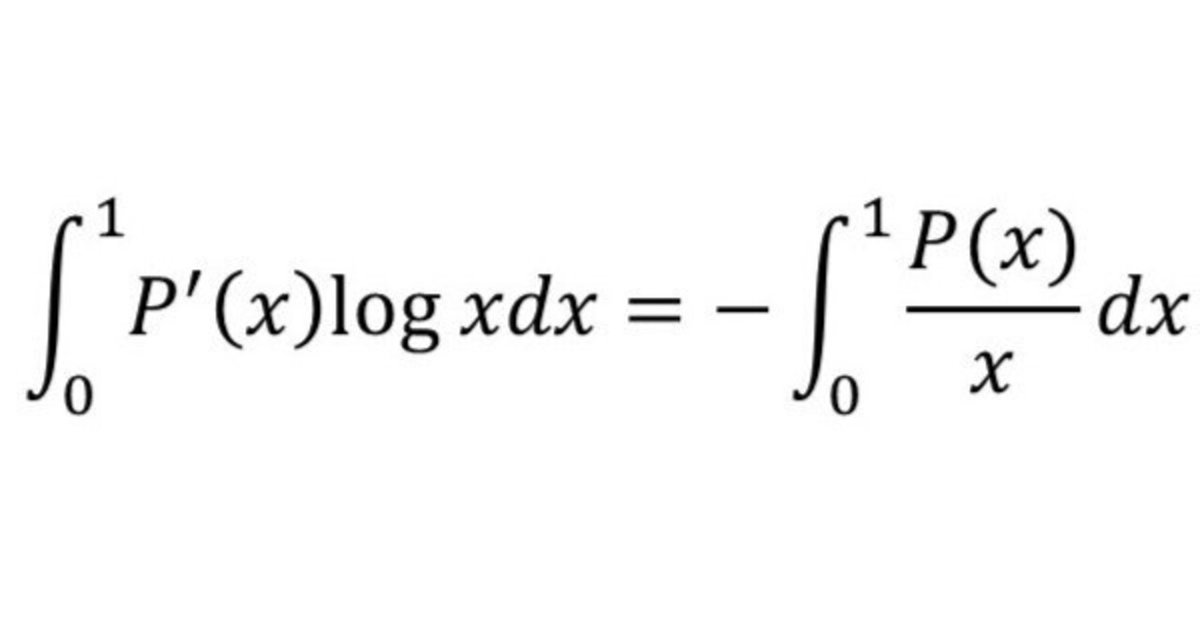
高校数学をプログラミングで解く（数学III編）「7-3 定積分の部分積分法」

マガジンリスト　＞　数学Ⅲ編 7.積分法　＞　7-3 定積分の部分積分法

はじめに

今回は、数学IIIで学ぶ「定積分の部分積分法」について、そのままでは数値積分が難しい定積分を、部分積分法を用いて数値計算できるような形にして計算することを考えてみます。

部分積分法

まず、定積分の部分積分法について解説しておきます。

定積分の部分積分法

① 

$$
\int_a^b f(x) g'(x) dx = \left[ f(x)g(x) \right]_a^b - \int_a^b f'(x)g(x)dx
$$

②

$$
\int_a^b f(x) dx = \left[ xf(x) \right]_a^b - \int_a^b x f'(x) dx
$$

定積分の数値計算を行うための部分積分の応用

今回は、定積分の数値計算を行うための部分積分法の応用として、次の定積分を計算することを考えてみます。

$$
\int_0^1 P'(x) \log x dx
$$

ただし、$${P'(x)}$$は定数項を含む$${x}$$の多項式とします。

数値計算を行うための問題点

この定積分を数値的に計算しようとした場合、一つ問題がおこります。それは、$${P'(x)}$$の定数項を$${C}$$とした場合、$${x \to +0}$$で被積分関数の定数項を含む部分$${C \log x}$$が発散してしまうことです。
記事『高校数学をプログラミングで解く（数学II編）「5-6 定積分（１）」』で解説した台形公式は、定積分を

$$
\int_a^b f(x) dx = \sum_{i=0}^{n-1} \left[ \frac{1}{2} ( f(x_i) + f(x_i+1) ) \Delta x \right]
$$

と、台形の面積の和で置き換えて計算するものでした。ところが今回の定積分では、$${x_0=0}$$で被積分関数$${f(x) = P'(x) \log x}$$が発散してしまうので、台形公式を用いた定積分の数値計算はできないように見えます。

部分積分法を用いて数値計算できるようにする

この定積分は数値計算しようとすると計算できないように見えますが、部分積分法を用いて定積分を書き換えてみると数値計算ができるような形に変形することができます。
この定積分は、部分積分法を利用して次のように変形することができます。

$$
\int_0^1 P'(x) \log x dx = \left[ P(x) \log x \right]_0^1 -\int_0^1 \frac{P(x)}{x} dx
$$

$${P'(x)}$$は$${x}$$の多項式ですので、$${P(x)}$$は定数項を持たない$${x}$$の多項式となります。そのため、右辺の第1項は$${0}$$となります。
また、$${P(x)/x}$$も$${x}$$の多項式になりますので、右辺の第２項は数値積分することができる形となっています。

数値計算を行うためのプログラム

記事『高校数学をプログラミングで解く（数学II編）「5-6 定積分（１）」』で解説した台形公式やそのとき作成したスケッチ「calc_definite_integral」を再利用して、今回の定積分の値を数値計算するためのプログラムを作成していきます。以下の zip ファイルをダウンロードして展開または解凍してください。

calc_definite_integral.zip

1.09 KB

ファイルダウンロードについて

ダウンロード

そして、スケッチの名前（フォルダ名）を「calc_definite_integral3」と変更し、またスケッチ「calc_definite_integral3」内の「calc_definite_integral.pde」ファイルの名前を「calc_definite_integral3.pde」に変更します。そして、pdeファイル「calc_definite_integral3.pde」をダブルクリックしてスケッチ「calc_definite_integral3」の開発環境ウィンドウを立ち上げ、そのテキストエリアのソースコードを以下で書き換えます。

なお、このプログラムでは、

$$
P'(x) = 2x+1
$$

として作成していきます。つまり、

$$
P(x) = x^2+x, \ \ \ \ \frac{P(x)}{x} = x+1
$$

となります。

// 定積分を台形公式を利用して計算するプログラム
void setup(){

  // 定積分を計算して結果をコンソールに出力 
  float l = 0.0; // 積分領域の下限
  float r = 1.0; // 積分領域の上限
  float res = -trapezoidal_rule(l,r);
  println(res);
}

// 被積分関数
float f(
  float x 
){
  return x+1.0;
}

// 被積分関数 f に対する定積分を計算する関数
float trapezoidal_rule(
  float l, // 積分領域の下限
  float r // 積分領域の上限
){
  float dx = 0.01;
  int division_num = (int)((r-l)/dx);
  float x, y1, y2;
  float dintegral = 0.0;
  for(int i=0; i<division_num; i++){
    x = l + i*dx;
    y1 = f(x);
    y2 = f(x+dx);
    dintegral = dintegral + (y1+y2)*dx/2.0;
  }
  return dintegral;
}

ソースコード1　部分積分法適用後の定積分を数値計算するためのプログラム

ソースコード1では、多項式$${P(x)/x}$$を関数 f で表しています。また、右辺の第２項のマイナス符号は、

float res = -trapezoidal_rule(l,r);

と、数値積分した後に与えるようにしています。

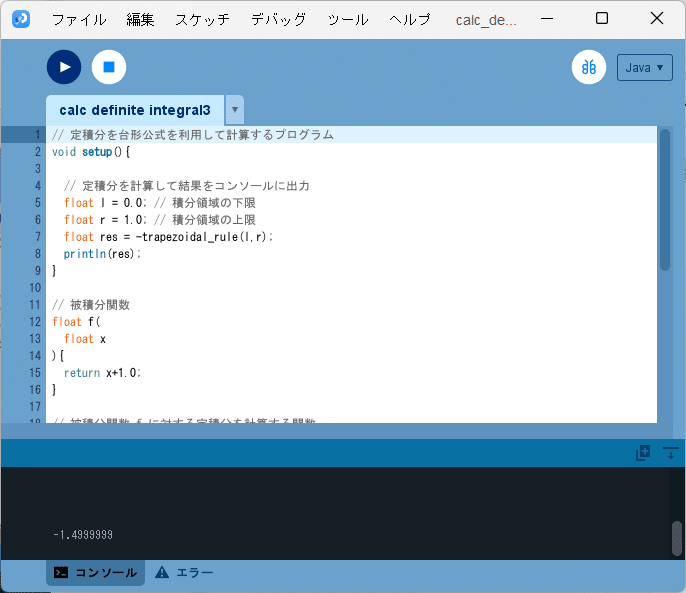
ソースコード1を、スケッチ「calc_definite_integral3」の「calc_definite_integral3」タブのテキストエディタ部分に書いて実行すると、図1のように、開発環境ウィンドウのコンソールに、

-1.4999999

と出力されます。

図1　スケッチ「calc_definite_integral3」の実行結果

定積分の解析的な計算結果は

$$
\int_0^1 P'(x) \log x dx = -\int_0^1 \frac{P(x)}{x} dx = -\int_0^1 (x+1) dx = -\left[ \frac{x^2}{2} + x \right]_0^1 = -\frac{3}{2}
$$

となりますので、今回は丸め誤差程度での結果が得られていることがわかります。

まとめ

今回は、数学IIIで学ぶ「定積分の部分積分法」について、そのままでは数値積分が難しい定積分を、部分積分法を用いて数値計算できるような形にして計算することを考えてみました。
実際、被積分関数が$${P'(x) \log x}$$（ただし、$${P'(x)}$$は定数項を含む$${x}$$の多項式）の場合、$${x=0}$$のところで被積分関数は発散してしまいますが、部分積分を行うことで、被積分関数が$${P(x)/x}$$に変わるため、この定積分が数値計算できる形に書き換えることができました。
部分積分法は、定積分の解析的な計算に役立つだけでなく、今回のように、そのままでは数値計算が難しいような定積分も計算できるような形に書き換えるときにも有用な方法です。記事『高校数学をプログラミングで解く（数学III編）「7-2 定積分の置換積分法」』のときと同様、今後、このような積分を計算する機会もあるかもしれませんので、こちらも頭の片隅に記憶しておいてください。

読んだ感想などをお寄せください

本記事を読んだ感想や質問などを以下のお問い合せフォームからお寄せください。感想、質問をいただいた方には本記事の演習問題の解答をプレゼントします。（お問合せフォームの本文に、本記事のタイトルを入れてください。）

お問い合わせ | note（ノート）

参考文献

改訂版 教科書傍用 スタンダード・オリジナル 数学III（数研出版、ISBN9784410209567）

演習問題

次の定積分を数値計算するプログラムを作成してください。

$$
\int_0^1 \sqrt{\frac{x+1}{x}} dx
$$

演習問題の解答例