高校数学をプログラミングで解く（数学I編）「1-2 ２次関数のグラフ」

割引あり

MK's papa

2023年11月9日 03:58

マガジンリスト　＞　数学Ⅰ編 1.２次関数　＞　1-2 ２次関数のグラフ

はじめに

今回は、数学Iで学ぶ「２次関数のグラフ」について、２次関数のグラフとともにその２次関数の軸と頂点を描くプログラムを作成します。

２次関数（一般形）のグラフを描く

記事『高校数学をプログラミングで解く（数学I編）「1-1 関数とグラフ」』では、２次関数$${y=x^2+4x+3}$$のグラフを描くプログラムを作成しました。ここでは、２次関数の一般形

$$
y=ax^2+bx+c (a \neq 0）
$$

を関数化して、より一般的な２次関数のグラフを描けるようにプログラムを書き換えておきます。

２次関数（一般形）のプログラム

２次関数の一般形のプログラムは以下のようになります。

// ２次関数の一般形
float quadraticfunction(
  float a, // 2次の係数
  float b, // 1次の係数
  float c, // 定数項
  float x
){
  return a*x*x + b*x + c;
}

今回は２次関数の一般形の係数$${a, b, c}$$をプログラムの関数の引数として与えています。

２次関数（一般形）を描くプログラム

上記の２次関数の一般形のプログラムを利用して、今度は２次関数のグラフを描くプログラムを作成します。なお、グラフを描くためには係数$${a,b,c}$$の値を決める必要がありますが、今回は

$$
a=1, \ b=4, \ c=3
$$

としています。つまり、記事『高校数学をプログラミングで解く（数学I編）「1-1 関数とグラフ」』で利用した２次関数$${y=x^2+4x+3}$$と同じものを描きます。

// ２次関数の一般形y=ax^2+bx+cのグラフを描く
void setup(){
  size(500,500);
  noLoop();
  float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
  float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで 
  setAxes(x_range, y_range); // 座標軸の準備
  
  noFill();
  stroke(0,0,0);
  
  // グラフの定義域
  float x_l = -x_range; // 定義域の左端
  float x_r = x_range; // 定義域の右端
  int plot_num = 200; // グラフを描くための頂点の個数  
  
  // ２次関数の係数
  float a = 1.0;
  float b = 4.0;
  float c = 3.0;
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標
  beginShape();
  for(int i=0; i<=plot_num; i++){
    x = x_l + (x_r - x_l) / plot_num * i; // 関数のx座標
    y = quadraticfunction(a, b, c, x); // 関数の値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();
  
}

// ２次関数の一般形
float quadraticfunction(
  float a, // 2次の係数
  float b, // 1次の係数
  float c, // 定数項
  float x
){
  return a*x*x + b*x + c;
}

ソースコード1　２次関数の一般形$${y=ax^2+bx+c}$$を描くプログラム

プログラムは、記事『高校数学をプログラミングで解く（数学I編）「1-0-2 グラフを描くための準備（その2）」』で作成したスケッチ「drawFunction」を再利用します。以下の zip ファイルをダウンロードして展開または解凍してください。

そして、スケッチの名前（フォルダ名）を「drawQuadraticFunctionStandardForm」と変更し、またスケッチ「drawQuadraticFunctionStandardForm」内の「drawFunction.pde」ファイルの名前を「drawQuadraticFunctionStandardForm.pde」に変更します。そして、pdeファイル「drawQuadraticFunctionStandardForm.pde」をダブルクリックしてスケッチ「drawQuadraticFunctionStandardForm」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「drawQuadraticFunctionStandardForm」タブを選択し、そのテキストエリアのソースコードを上記のソースコード1で書き換えます。
このプログラムを実行すると、図1のように、実行ウィンドウのキャンバスに２次関数のグラフが描かれます。

２次関数の軸と頂点を描く

次に、２次関数の軸と頂点を求めて、それらを２次関数のグラフとともに描くプログラムを作成していきます。

２次関数の軸と頂点を求める

２次関数の一般形$${y=ax^2+bx+c}$$の軸と頂点を求めるためには、この関数を平方完成させます。

$$
y = ax^2+bx+c = a \left( x + \frac{b}{2a} \right)^2 - \frac{b^2-4ac}{4a}
$$

この結果から、２次関数の軸は

$$
x=-\frac{b}{2a}
$$

となり、頂点は

$$
\left( -\frac{b}{2a}, -\frac{b^2-4ac}{4a} \right)
$$

となります。

２次関数の軸と頂点を描くプログラム

それでは、２次関数のグラフとともに２次関数の軸と頂点を描くプログラムを作成します。なお、プログラムでは、

$$
p= -\frac{b}{2a}, \ q = -\frac{b^2-4ac}{4a}
$$

とおいて、軸は$${x=p}$$、頂点は$${(p,q)}$$となるようにしています。
また、軸や頂点を描く際には、キャンバス上の座標に変換することを忘れないようにします。

// ２次関数の一般形y=ax^2+bx+cのグラフを描く
void setup(){
  size(500,500);
  noLoop();
  float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
  float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで 
  setAxes(x_range, y_range); // 座標軸の準備
  
  noFill();
  stroke(0,0,0);
  
  // グラフの定義域
  float x_l = -x_range; // 定義域の左端
  float x_r = x_range; // 定義域の右端
  int plot_num = 200; // グラフを描くための頂点の個数  
  
  // ２次関数の係数
  float a = 1.0;
  float b = 4.0;
  float c = 3.0;
  
  // ２次関数の軸x=pと頂点(p,q)
  float p = -b/2.0/a;
  float q = -(b*b-4.0*a*c)/4.0/a;
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標
  beginShape();
  for(int i=0; i<=plot_num; i++){
    x = x_l + (x_r - x_l) / plot_num * i; // 関数のx座標
    y = quadraticfunction(a, b, c, x); // 関数の値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

  // 軸と頂点をキャンバス上の座標に変換
  float P, Q;
  P = width / 2.0 / x_range * p;
  Q = height / 2.0 / y_range * q;
  
  // ２次関数の軸を描画
  stroke(0,0,255);
  line(P, -height/2.0, P, height/2.0);
  
  // ２次関数の頂点を描画
  stroke(255,0,0);
  strokeWeight(5);
  point(P, Q);
  
}

// ２次関数の一般形
float quadraticfunction(
  float a, // 2次の係数
  float b, // 1次の係数
  float c, // 定数項
  float x
){
  return a*x*x + b*x + c;
}

ソースコード2　２次関数のグラフとともに軸と頂点を描くプログラム

そして、スケッチの名前（フォルダ名）を「drawQuadraticFunctionwithAxisandVertex」と変更し、またスケッチ「drawQuadraticFunctionwithAxisandVertex」内の「drawFunction.pde」ファイルの名前を「drawQuadraticFunctionwithAxisandVertex.pde」に変更します。そして、pdeファイル「drawQuadraticFunctionwithAxisandVertex.pde」をダブルクリックしてスケッチ「drawQuadraticFunctionwithAxisandVertex」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「drawQuadraticFunctionwithAxisandVertex」タブを選択し、そのテキストエリアのソースコードを上記のソースコード2で書き換えます。
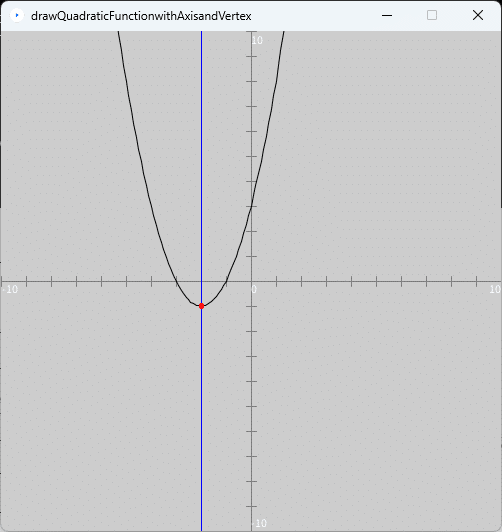
このプログラムを実行すると、図2のように、実行ウィンドウのキャンバスに２次関数のグラフとその軸（青色の線）と頂点（赤色の点）が描かれます。

まとめ

今回は、数学Iで学ぶ「２次関数のグラフ」について、２次関数のグラフとともにその２次関数の軸と頂点を描くプログラムを作成しました。
記事『高校数学をプログラミングで解く（数学I編）「1-1 関数とグラフ」』では、２次関数$${y=x^2+4x+3}$$のグラフを描くプログラムを作成しました。この記事では、２次関数の一般形$${y=ax^2+bx+c}$$のグラフが描けるようにプログラムを修正しました。また、２次関数の軸$${x=p}$$と頂点$${(p,q)}$$は、一般形の係数を用いて、

$$
p= -\frac{b}{2a}, \ q = -\frac{b^2-4ac}{4a}
$$

と計算できますので、これらの式を用いて２次関数とともに軸と頂点も描くプログラムを作成しました。
このプログラムのポイントは、こちらが行うことは係数$${a,b,c}$$の値を決めることだけにしたことです。軸、頂点を描くためには、具体的な値が必要になってきますが、軸や頂点の計算は計算式を与えることで自動的にプログラムが行うので、手計算で具体的な値を求める必要はありません。
一般に、プログラムを書くときにはこちらで具体的に与える値は最小限に抑え、それらの値から必要な値を求めるときは、数式などをプログラムにしてコンピュータに計算させることが一般的です。
このような書き方はプログラムを書いていくうちに覚えていきますので、少しずつ慣れていってください。

読んだ感想などをお寄せください

本記事を読んだ感想や質問などを以下のお問い合せフォームからお寄せください。感想、質問をいただいた方には本記事の演習問題の解答をプレゼントします。（お問合せフォームの本文に、本記事のタイトルを入れてください。）

参考文献

改訂版教科書傍用スタンダード数学I（数研出版、ISBN9784410209178）

演習問題

次の２次関数のグラフを軸と頂点と共に描いてみてください。
(1)　$${y=x^2-2x-2}$$
(2)　$${y=2x^2-8x+1}$$
(3)　$${y=\frac{1}{2} x^2 + 3x +3}$$

演習問題の解答例

ここから先は

718字 / 3画像

ログイン

この記事が気に入ったらチップで応援してみませんか？