
高校数学をプログラミングで解く(数学B編)「2-0-2 3次元空間での座標軸を準備する」
マガジンリスト > 数学B編 2.空間のベクトル > 2-0-2 3次元空間での座標軸を準備する
はじめに
今回はキャンバス上に設定された座標軸を空間ベクトルを用いて表し、その上でマウス操作によりその3次元空間での座標軸を$${z}$$軸周りで回転させるプログラムを作成します。
3次元空間での座標軸を準備する
記事『高校数学をプログラミングで解く(数学B編)「2-0-1 空間ベクトルを描く」』で、空間ベクトルを描くための関数 arrow3D を作成しました。ここではこの arrow3D 関数を用いて3次元空間での座標軸を描きます。
3次元空間での座標軸を描くプログラム
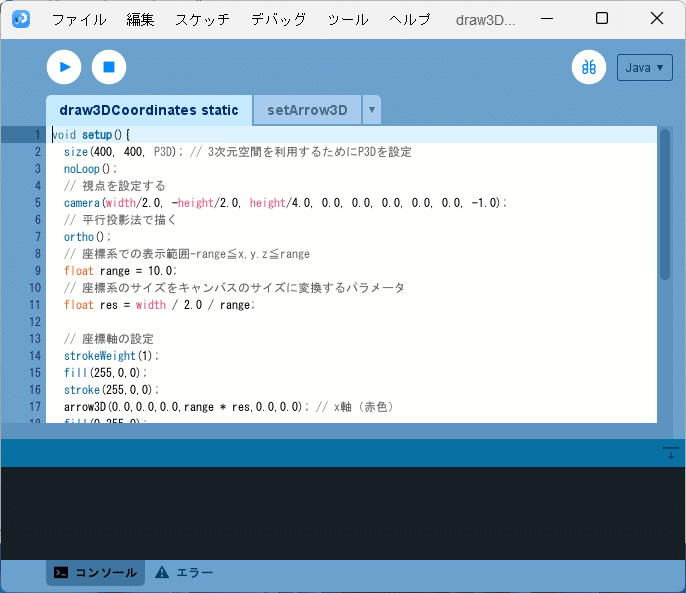
記事『高校数学をプログラミングで解く(数学B編)「2-0-1 空間ベクトルを描く」』で利用したスケッチ「draw3DVector_test」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「draw3DCoordinates_static」と変更し、またスケッチ「draw3DCoordinates_static」内の「draw3DVector_test.pde」ファイルの名前を「draw3DCoordinates_static.pde」に変更します。そして、pdeファイル「draw3DCoordinates_static.pde」をダブルクリックしてスケッチ「draw3DCoordinates_static」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「draw3DCoordinates_static」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。
void setup(){
size(400, 400, P3D); // 3次元空間を利用するためにP3Dを設定
noLoop();
// 視点を設定する
camera(width/2.0, -height/2.0, height/4.0, 0.0, 0.0, 0.0, 0.0, 0.0, -1.0);
// 平行投影法で描く
ortho();
// 座標系での表示範囲-range≦x,y.z≦range
float range = 10.0;
// 座標系のサイズをキャンバスのサイズに変換するパラメータ
float res = width / 2.0 / range;
// 座標軸の設定
strokeWeight(1);
fill(255,0,0);
stroke(255,0,0);
arrow3D(0.0,0.0,0.0,range * res,0.0,0.0); // x軸(赤色)
fill(0,255,0);
stroke(0,255,0);
arrow3D(0.0,0.0,0.0,0.0,range * res,0.0); // y軸(緑色)
fill(0,0,255);
stroke(0,0,255);
arrow3D(0.0,0.0,0.0,0.0,0.0,range * res); // z軸(青色)
// 3Dベクトルを描く
strokeWeight(1);
fill(0,0,0);
stroke(0,0,0);
arrow3D(0.0,0.0,0.0,2.0*res,7.0*res,8.0*res);
}ソースコード1 3次元空間での座標軸を描くプログラム
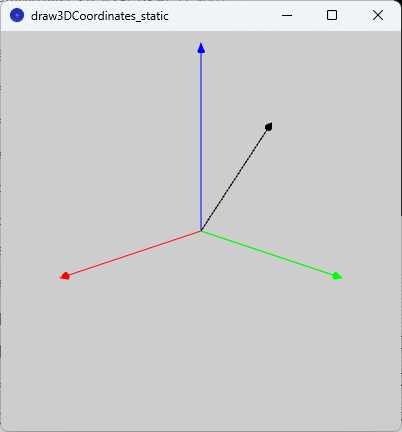
このスケッチ「draw3DCoordinates_static」を実行すると、図2のように実行ウィンドウのキャンバス上に$${x}$$軸を赤色の空間ベクトル、$${y}$$軸を緑色の空間ベクトル、$${z}$$軸を青色の空間ベクトルとして描かれます。
プログラムの解説
記事『高校数学をプログラミングで解く(数学B編)「2-0-1 空間ベクトルを描く」』で利用したスケッチ「draw3DVector_test」ではそれぞれの座標軸上に点列を並べていましたが、今回のプログラム(ソースコード1)では、これらの点列をそれぞれ空間ベクトルに置き換えたものになります。つまり、スケッチ「draw3DVector_test」の
// 点のサイズを設定
strokeWeight(10);
// 座標系の原点に点を打つ(黒色)
point(0.0,0.0,0.0);
// x軸上に点列を並べる(赤色)
stroke(255,0,0);
for(int i=1; i<=4; i++){
point(50.0*i,0.0,0.0);
}
// y軸上に点列を並べる(緑色)
stroke(0,255,0);
for(int i=1; i<=4; i++){
point(0.0,-50.0*i,0.0);
}
// z軸上に点列を並べる(青色)
stroke(0,0,255);
for(int i=1; i<=100; i++){
point(0.0,0.0,50.0*i);
}の部分を、スケッチ「draw3DCoordinates_static」では、
// 座標軸の設定
strokeWeight(1);
fill(255,0,0);
stroke(255,0,0);
arrow3D(0.0,0.0,0.0,range * res,0.0,0.0); // x軸(赤色)
fill(0,255,0);
stroke(0,255,0);
arrow3D(0.0,0.0,0.0,0.0,range * res,0.0); // y軸(緑色)
fill(0,0,255);
stroke(0,0,255);
arrow3D(0.0,0.0,0.0,0.0,0.0,range * res); // z軸(青色)に置き換えたものになっています。
なお、各座標軸を表す空間ベクトルは座標系の表示範囲を表すパラメータ range と同じ大きさを持っています。そのため、それらの空間ベクトルを描画する際の arrow3D 関数の引数には range に、座標系のサイズをキャンバスのサイズに変換するパラメータ res を掛けた値を入力します。
マウス操作で座標軸をz軸周りに回転させる
図2を見ると、3次元座標軸を描いたおかげで少し空間ベクトルらしく見えてきました。ただ、空間ベクトル(黒色)がどのような大きさでどの方向に向いているかというのは正直あまりよくわからないと思います。
3次元空間のベクトルを2次元平面上に描いているので、これは多少仕方がないことでもありますが、この空間ベクトルを別の方向から見たような図をいくつか用意できれば、この問題はある程度解決できそうです。
そこで、ここでは、3次元空間の座標系を$${z}$$軸周りに回転させることで、別の方向からも空間ベクトルを見ることができるようにしてみます。
マウス操作で座標軸をz軸周りに回転させるプログラム
上記で作成したスケッチ「draw3DCoordinates_static」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「draw3DCoordinates」と変更し、またスケッチ「draw3DCoordinates」内の「draw3DCoordinates_static.pde」ファイルの名前を「draw3DCoordinates.pde」に変更します。そして、pdeファイル「draw3DCoordinates.pde」をダブルクリックしてスケッチ「draw3DCoordinates」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「draw3DCoordinates」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。
float range; // 座標系での表示範囲-range≦x,y.z≦range
float res; // 座標系のサイズをキャンバスのサイズに変換するパラメータ
float angle = 0.0;
void setup(){
size(400, 400, P3D);
// noFill();
ortho();
range = 10.0;
res = width / 2.0 / range;
}
void draw(){
background(204); // 背景をグレーにする
// 視点を設定する
camera(width/2.0, -height/2.0, height/4.0, 0.0, 0.0, 0.0, 0.0, 0.0, -1.0);
// マウスボタンが押されたときの処理
if(mousePressed){
if( mouseButton == LEFT ){ // 左ボタンがおされたときはz軸時計周りに回転
angle = angle + 1.0;
} else if( mouseButton == RIGHT ){ // 右ボタンがおされたときはz軸反時計周りに回転
angle = angle -1.0;
} else {
}
}
// z軸周りに回転
rotateZ(radians(angle));
// 座標軸の設定
strokeWeight(1);
fill(255,0,0);
stroke(255,0,0);
arrow3D(0.0,0.0,0.0,range * res,0.0,0.0); // x軸(赤色)
fill(0,255,0);
stroke(0,255,0);
arrow3D(0.0,0.0,0.0,0.0,range * res,0.0); // y軸(緑色)
fill(0,0,255);
stroke(0,0,255);
arrow3D(0.0,0.0,0.0,0.0,0.0,range * res); // z軸(青色)
noFill();
stroke(0,0,0);
// 以下に図形を描いていく
// 3Dベクトルを描く
fill(0,0,0);
stroke(0,0,0);
arrow3D(0.0,0.0,0.0,2.0*res,7.0*res,8.0*res);
}ソースコード2 マウス操作で3次元空間での座標軸を$${z}$$軸周りに回転させるプログラム
このスケッチ「draw3DCoordinates」を実行すると、図3のように実行ウィンドウのキャンバス上に図2と同じものが描かれます。
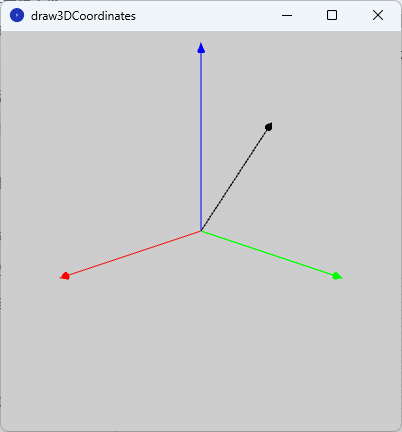
そして、このキャンバス上をマウスで左クリックしてみてください。座標軸が$${z}$$軸周りに時計回りに回転し始めます。また、右クリックしてみると、今度、座標軸が$${z}$$軸周りに反時計回りに回転します。この状態を図4に示しています。
図4のように、座標軸を$${z}$$軸周りで回転させることで、空間ベクトルの大きさや向きがある程度わかりやすくなったと思います。
プログラムの解説1「座標軸を動かす」
今回、座標軸や空間ベクトルを動かしています。プログラミング言語「Processing」で図形を動かす方法は、記事『高校数学をプログラミングで解く(準備編)「4-1 図形を動かす」』で解説していますので、詳細はそちらをご覧ください。
ソースコード1とソースコード2を見比べてみてください。まず、ソースコード1では、setup 関数内に記述していた
// 座標軸の設定
strokeWeight(1);
fill(255,0,0);
stroke(255,0,0);
arrow3D(0.0,0.0,0.0,range * res,0.0,0.0); // x軸(赤色)
fill(0,255,0);
stroke(0,255,0);
arrow3D(0.0,0.0,0.0,0.0,range * res,0.0); // y軸(緑色)
fill(0,0,255);
stroke(0,0,255);
arrow3D(0.0,0.0,0.0,0.0,0.0,range * res); // z軸(青色)
// 3Dベクトルを描く
strokeWeight(1);
fill(0,0,0);
stroke(0,0,0);
arrow3D(0.0,0.0,0.0,2.0*res,7.0*res,8.0*res);の部分を、ソースコード2では、draw 関数内に移動しています。これにより、座標軸を回転させる準備ができました。また、ソースコード1の setup 関数内に記述していた
// 座標系での表示範囲-range≦x,y.z≦range
float range = 10.0;
// 座標系のサイズをキャンバスのサイズに変換するパラメータ
float res = width / 2.0 / range;の部分を、ソースコード2では、これらの変数の宣言を setup 関数の外(プログラムの先頭)に移動し、変数の初期化のみを setup 関数内で行うようにしています。これは、変数 range や res を setup 関数と draw 関数の両方で利用するため、変数のスコープを調整しています。
プログラムの解説2「マウス操作」
今回、スケッチ「draw3DCoordinates」の実行結果は、その実行ウィンドウのキャンバス上を、左クリックすると座標軸が$${z}$$軸周りに時計回りに回転し、右クリックすると座標軸が$${z}$$軸周りに反時計回りに回転するようにしています。これは、ソースコード2の draw 関数内に記述した、
// マウスボタンが押されたときの処理
if(mousePressed){
if( mouseButton == LEFT ){ // 左ボタンがおされたときはz軸時計周りに回転
angle = angle + 1.0;
} else if( mouseButton == RIGHT ){ // 右ボタンがおされたときはz軸反時計周りに回転
angle = angle -1.0;
} else {
}
}
// z軸周りに回転
rotateZ(radians(angle));の部分で行っています。つまり、マウスの左ボタンが押された場合、$${z}$$軸周りの回転角度 angle が1°ずつ増えていき、マウスの右ボタンが押された場合、angle が1°ずつ減っていくようになっており、その回転角度に合わせて$${z}$$軸周りに座標軸を回転させています(もう少し正確に言えば、$${z}$$軸周りに”座標系”を回転してその回転した座標系に合わせて座標軸を表示しています)。なお、変数 angle は draw 関数が画像を更新するごとに変えることができるように、draw 関数の外(プログラムの先頭)で宣言と初期化を行っています。
マウス操作については、記事『高校数学をプログラミングで解く(準備編)「4-2 マウス操作」』で解説していますので、詳細はそちらをご覧ください。
まとめ
今回はキャンバス上に設定された座標軸を空間ベクトルを用いて表し、その上でマウス操作によりその3次元空間での座標軸を$${z}$$軸周りで回転させるプログラムを作成しました。
3次元空間の図形を2次元平面上に描くため静止画ではよくわからなかったことも、図形を動かして別の視点で見ることで少しわかりやすくなったのではないでしょうか。
今後、空間ベクトルに限らず、空間的な図形を表すためにスケッチ「draw3DCoordinates」を利用していきます。具体的には、ソースコード2のdraw関数内に
noFill();
stroke(0,0,0);
// 以下に図形を描いていくと記述した部分の下に、空間図形を描いていくことになります。今後の記事でご確認ください。
参考文献
Processingをはじめよう 第2版(オライリー・ジャパン、オーム社、ISBN9784873117737)
