高校数学をプログラミングで解く（数学I編）「1-0-1 グラフを描くための準備（その1）」

マガジンリスト　＞　数学Ⅰ編 1.２次関数　＞　1-0-1 グラフを描くための準備（その1）

はじめに

今回は、「高校数学をプログラミングで解く」で、今後実行ウィンドウのキャンバス上にグラフを描いていくための準備をします。
プログラミング言語「Processing」には、グラフを描くためのツールなどは準備されていないようです。そのため、座標軸などを自作していきます。

グラフを描くための座標軸を準備する

グラフを描く例として、２次関数

$$
y=x^2+4x+3
$$

を考えていきます。最終的に描きたいグラフは図1のようなものです。

図1　グラフを描く

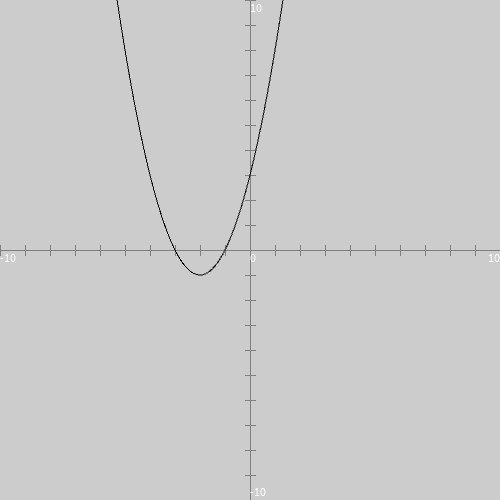
以下で、このグラフを描くための座標軸を準備する方法を順番に解説していきます。

座標系を設定する

まず、座標系を設定します。座標系は記事『高校数学をプログラミングで解く（数学Ａ編）「2-0 高校数学に適した座標系の準備」』で設定したものを利用します。つまり、原点をキャンバスの中央にとり、高校数学に合わせて、右向きに$${x}$$軸の正の向き、上向きに$${y}$$軸の正の向きとする座標系になるようにします。

// 関数のグラフを描く
void setup(){
  size(500, 500); // キャンバスの大きさを指定する
  translate(width/2, height/2); // 座標の中心をキャンバスの中心に移動する
  scale(1,-1); // y軸正の向きを下向きから上向きに反転する
  
}

ソースコード1　キャンバスに座標系を準備する

ソースコード1を、Processingの開発環境ウィンドウを開いて（スケッチ名を「drawGraph」としています）、テキストエディタ部分に書いて実行すると、図2のように、実行ウィンドウに500×500サイズのキャンバスが準備されます。

図2　キャンバスの準備

座標軸を描く

次は、図2のキャンバスに座標軸を描きます。座標軸はline関数を利用して描きますが、グラフと座標軸を区別するために色をグレーに設定しています。

// 関数のグラフを描く
void setup(){
  size(500, 500); // キャンバスの大きさを指定する
  translate(width/2, height/2); // 座標の中心をキャンバスの中心に移動する
  scale(1,-1); // y軸正の向きを下向きから上向きに反転する

  stroke(128,128,128); // 線の色をグレーにする
  
  // 軸の設定
  line(-width/2, 0.0, width/2, 0.0); // x軸
  line(0.0, -height/2, 0.0, height/2); // y軸
  
}

ソースコード2　座標軸を描く

スケッチ「drawGraph」のテキストエディタ部分をソースコード2に書き換えて実行すると、図3のように、キャンバス上に座標軸が描かれます。

図3　キャンバス上に座標軸が描かれる

座標軸に目盛りを付ける

次は、図3で描いた座標軸に目盛りを付けていきます。目盛りは$${x}$$軸と$${y}$$軸がそれぞれ20等分されるように付けていきます。また、目盛りの幅は10ピクセルに設定し、line関数を利用して描いていきます。

// 関数のグラフを描く
void setup(){
  size(500, 500); // キャンバスの大きさを指定する
  translate(width/2, height/2); // 座標の中心をキャンバスの中心に移動する
  scale(1,-1); // y軸正の向きを下向きから上向きに反転する

  stroke(128,128,128); // 線の色をグレーにする
  
  // 軸の設定
  line(-width/2, 0.0, width/2, 0.0); // x軸
  line(0.0, -height/2, 0.0, height/2); // y軸
  
  // 目盛りの設定
  float scale_size = 10.0; // 目盛りの幅（pixel単位）
  int scale_num = 20; // 目盛りの数
  float pos_scale; // 目盛りの位置
  
  // x軸に目盛りを設定する
  for(int i=0; i<=scale_num; i++){
    pos_scale = -width/2.0 + i * width / scale_num;
    line(pos_scale, -scale_size/2.0, pos_scale, scale_size/2.0);
  }
  // y軸に目盛りを設定する
  for(int i=0; i<scale_num; i++){
    pos_scale = -height/2.0 + i * height / scale_num;
    line(-scale_size/2.0, pos_scale, scale_size/2.0, pos_scale);
  }
  
}

ソースコード3　座標軸に目盛りを設定する

スケッチ「drawGraph」のテキストエディタ部分をソースコード3に書き換えて実行すると、図4のように、座標軸に目盛りが描かれます。

図4　座標軸に目盛りを設定

関数のグラフの描画範囲を設定する

次は、関数のグラフの描画範囲を設定します。
図1では、関数のグラフの$${x}$$方向の描画範囲を$${-10}$$から$${10}$$までとし、$${y}$$方向の描画範囲を$${-10}$$から$${10}$$までとしています。それに合わせて、各軸の両端にそれらの上限と下限（今回は$${10}$$や$${-10}$$）の値を表示しています。なお、文字の描画に関しては記事『高校数学をプログラミングで解く（準備編）「3-1 キャンバス上にテキスト出力」』を見てください。

// 関数のグラフを描く
void setup(){
  size(500, 500); // キャンバスの大きさを指定する
  translate(width/2, height/2); // 座標の中心をキャンバスの中心に移動する
  scale(1,-1); // y軸正の向きを下向きから上向きに反転する

  stroke(128,128,128); // 線の色をグレーにする
  
  // 軸の設定
  line(-width/2, 0.0, width/2, 0.0); // x軸
  line(0.0, -height/2, 0.0, height/2); // y軸
  
  // 目盛りの設定
  float scale_size = 10.0; // 目盛りの幅（pixel単位）
  int scale_num = 20; // 目盛りの数
  float pos_scale; // 目盛りの位置
  
  // x軸に目盛りを設定する
  for(int i=0; i<=scale_num; i++){
    pos_scale = -width/2.0 + i * width / scale_num;
    line(pos_scale, -scale_size/2.0, pos_scale, scale_size/2.0);
  }
  // y軸に目盛りを設定する
  for(int i=0; i<scale_num; i++){
    pos_scale = -height/2.0 + i * height / scale_num;
    line(-scale_size/2.0, pos_scale, scale_size/2.0, pos_scale);
  }

  float x_range = 10.0; // グラフの表示範囲を-x_rangeからx_rangeまでとする
  float y_range = 10.0; // グラフの表示範囲を-y_rangeからy_rangeまでとする

  // x軸とy軸の両端にxとyのそれぞれの範囲を表す数字を表示
  textAlign(LEFT, BOTTOM);
  text("0", 0.0,0.0);
  textAlign(LEFT, BOTTOM);
  text(int(-x_range), -width/2.0, 0.0);
  textAlign(RIGHT, BOTTOM);
  text(int(x_range), width/2.0, 0.0);
  textAlign(LEFT, BOTTOM);
  text(int(-y_range), 0.0, height/2.0);
  textAlign(LEFT, TOP);
  text(int(y_range), 0.0, -height/2.0);
  
}

ソースコード4　グラフの描画範囲を設定（反転失敗）

スケッチ「drawGraph」のテキストエディタ部分をソースコード4に書き換えて実行すると、図5のように、グラフの描画範囲が表示されますが、よくみると$${y}$$軸方向の$${10}$$と$${-10}$$とが入れ替わっており、また文字が上下反転しています。

図5　文字が反転してる

図5のように文字が反転している原因は、座標系を設定した際、高校数学に合わせて上向きに$${y}$$軸の正の向きとする座標系にするために導入した

  scale(1,-1); // y軸正の向きを下向きから上向きに反転する

によるものです。
これを解消するためには、座標軸やグラフの描画範囲の設定を行ったあと、scale関数を呼び出して上向きを$${y}$$軸の正の向きとするようにします。

// 関数のグラフを描く
void setup(){
  size(500, 500); // キャンバスの大きさを指定する
  translate(width/2, height/2); // 座標の中心をキャンバスの中心に移動する

  stroke(128,128,128); // 線の色をグレーにする
  
  // 軸の設定
  line(-width/2, 0.0, width/2, 0.0); // x軸
  line(0.0, -height/2, 0.0, height/2); // y軸
  
  // 目盛りの設定
  float scale_size = 10.0; // 目盛りの幅（pixel単位）
  int scale_num = 20; // 目盛りの数
  float pos_scale; // 目盛りの位置
  
  // x軸に目盛りを設定する
  for(int i=0; i<=scale_num; i++){
    pos_scale = -width/2.0 + i * width / scale_num;
    line(pos_scale, -scale_size/2.0, pos_scale, scale_size/2.0);
  }
  // y軸に目盛りを設定する
  for(int i=0; i<scale_num; i++){
    pos_scale = -height/2.0 + i * height / scale_num;
    line(-scale_size/2.0, pos_scale, scale_size/2.0, pos_scale);
  }

  float x_range = 10.0; // グラフの表示範囲を-x_rangeからx_rangeまでとする
  float y_range = 10.0; // グラフの表示範囲を-y_rangeからy_rangeまでとする

  // x軸とy軸の両端にxとyのそれぞれの範囲を表す数字を表示
  textAlign(LEFT, TOP);
  text("0", 0.0,0.0);
  textAlign(LEFT, TOP);
  text(int(-x_range), -width/2.0, 0.0);
  textAlign(RIGHT, TOP);
  text(int(x_range), width/2.0, 0.0);
  textAlign(LEFT, BOTTOM);
  text(int(-y_range), 0.0, height/2.0);
  textAlign(LEFT, TOP);
  text(int(y_range), 0.0, -height/2.0);
 
  scale(1,-1); // y軸正の向きを下向きから上向きに反転する

}

ソースコード5　グラフの描画範囲を設定

スケッチ「drawGraph」のテキストエディタ部分をソースコード5に書き換えて実行すると、図6のように、今度は正しい位置にグラフの描画範囲が表示されます。

図6　グラフの描画範囲を設定する

以上で、グラフを描くための座標軸の準備は完了です。

2次関数のグラフを描く

次に、2次関数のグラフを描いていきます。

２次関数の準備

まず、２次関数$${y=x^2+4x+3}$$を以下のようにプログラムの関数として準備します。

// 2次関数
float quadraticfunction(
  float x
){
  return x*x + 4.0*x + 3.0;
}

ソースコード6　2次関数をプログラムの関数として準備

関数のグラフを描く

では、2次関数をソースコード5で準備した座標軸を基準として描いていきます。
グラフは記事『高校数学をプログラミングで解く（準備編）「2-3 Processingで多角形を描く」』で紹介した方法を応用して描きます。つまり、2次関数$${y=x^2+4x+3}$$上の点$${(x,y)}$$を関数の定義域$${-10 \leq x \leq 10}$$内で等間隔に取っていき、それらの頂点を順に結んでいくことでグラフを描いていきます。今回は200個の頂点を取ります。
ソースコード5に関数のグラフを描くためのプログラムを追加していきます。

// 関数のグラフを描く
void setup(){
  size(500, 500); // キャンバスの大きさを指定する
  translate(width/2, height/2); // 座標の中心をキャンバスの中心に移動する

  stroke(128,128,128); // 線の色をグレーにする
  
  // 軸の設定
  line(-width/2, 0.0, width/2, 0.0); // x軸
  line(0.0, -height/2, 0.0, height/2); // y軸
  
  // 目盛りの設定
  float scale_size = 10.0; // 目盛りの幅（pixel単位）
  int scale_num = 20; // 目盛りの数
  float pos_scale; // 目盛りの位置
  
  // x軸に目盛りを設定する
  for(int i=0; i<=scale_num; i++){
    pos_scale = -width/2.0 + i * width / scale_num;
    line(pos_scale, -scale_size/2.0, pos_scale, scale_size/2.0);
  }
  // y軸に目盛りを設定する
  for(int i=0; i<scale_num; i++){
    pos_scale = -height/2.0 + i * height / scale_num;
    line(-scale_size/2.0, pos_scale, scale_size/2.0, pos_scale);
  }

  float x_range = 10.0; // グラフの表示範囲を-x_rangeからx_rangeまでとする
  float y_range = 10.0; // グラフの表示範囲を-y_rangeからy_rangeまでとする

  // x軸とy軸の両端にxとyのそれぞれの範囲を表す数字を表示
  textAlign(LEFT, TOP);
  text("0", 0.0,0.0);
  textAlign(LEFT, TOP);
  text(int(-x_range), -width/2.0, 0.0);
  textAlign(RIGHT, TOP);
  text(int(x_range), width/2.0, 0.0);
  textAlign(LEFT, BOTTOM);
  text(int(-y_range), 0.0, height/2.0);
  textAlign(LEFT, TOP);
  text(int(y_range), 0.0, -height/2.0);
 
  scale(1,-1); // y軸正の向きを下向きから上向きに反転する

  // グラフの定義域
  float x_min = -x_range;
  float x_max = x_range;
  int plot_num = 200; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 頂点の座標 
  beginShape();
  for(int i=0; i<=plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // 頂点のx座標
    y = quadraticfunction(x); // 頂点のy座標（関数の値）
    vertex(x,y);
  }
  endShape();

}

// 2次関数
float quadraticfunction(
  float x
){
  return x*x + 4.0*x + 3.0;
}

ソースコード7　関数のグラフを描くプログラム

スケッチ「drawGraph」のテキストエディタ部分をソースコード7に書き換えて実行すると、図7のように、グラフが描画されます。

図7　関数のグラフを描画

図7には2次関数のような図形が描かれていますが、
・2次関数のグラフの中身が白色に塗り潰されている
・座標軸とグラフのスケールがあっていない（図1と図7を比較）
など、おかしな点がいくつかあります。以下でこれらを修正していきます。

プログラムの修正1「グラフの塗りつぶしの解消」

修正の1つ目として、グラフの中身を塗りつぶさないようにします。これにはnoFill関数を利用します。また、ついでに座標軸と区別するために、グラフの線の色は黒色になるようにstroke関数を利用して調整しておきます。

// 関数のグラフを描く
void setup(){
  size(500, 500); // キャンバスの大きさを指定する
  translate(width/2, height/2); // 座標の中心をキャンバスの中心に移動する

  stroke(128,128,128); // 線の色をグレーにする
  
  // 軸の設定
  line(-width/2, 0.0, width/2, 0.0); // x軸
  line(0.0, -height/2, 0.0, height/2); // y軸
  
  // 目盛りの設定
  float scale_size = 10.0; // 目盛りの幅（pixel単位）
  int scale_num = 20; // 目盛りの数
  float pos_scale; // 目盛りの位置
  
  // x軸に目盛りを設定する
  for(int i=0; i<=scale_num; i++){
    pos_scale = -width/2.0 + i * width / scale_num;
    line(pos_scale, -scale_size/2.0, pos_scale, scale_size/2.0);
  }
  // y軸に目盛りを設定する
  for(int i=0; i<scale_num; i++){
    pos_scale = -height/2.0 + i * height / scale_num;
    line(-scale_size/2.0, pos_scale, scale_size/2.0, pos_scale);
  }

  float x_range = 10.0; // グラフの表示範囲を-x_rangeからx_rangeまでとする
  float y_range = 10.0; // グラフの表示範囲を-y_rangeからy_rangeまでとする

  // x軸とy軸の両端にxとyのそれぞれの範囲を表す数字を表示
  textAlign(LEFT, TOP);
  text("0", 0.0,0.0);
  textAlign(LEFT, TOP);
  text(int(-x_range), -width/2.0, 0.0);
  textAlign(RIGHT, TOP);
  text(int(x_range), width/2.0, 0.0);
  textAlign(LEFT, BOTTOM);
  text(int(-y_range), 0.0, height/2.0);
  textAlign(LEFT, TOP);
  text(int(y_range), 0.0, -height/2.0);
 
  scale(1,-1); // y軸正の向きを下向きから上向きに反転する

  noFill(); // グラフの中身を塗りつぶさない
  stroke(0,0,0); // グラフの線の色を黒色に設定

  // グラフの定義域
  float x_min = -x_range;
  float x_max = x_range;
  int plot_num = 200; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 頂点の座標
  beginShape();
  for(int i=0; i<=plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // 頂点のx座標
    y = quadraticfunction(x); // 頂点のy座標（関数の値）
    vertex(x,y);
  }
  endShape();

}

// 2次関数
float quadraticfunction(
  float x
){
  return x*x + 4.0*x + 3.0;
}

ソースコード8　関数のグラフを描くプログラム（修正版1）

スケッチ「drawGraph」のテキストエディタ部分をソースコード8に書き換えて実行すると、図8のように、中身が塗りつぶされず線が黒色のグラフが描画されます。

図8　関数のグラフを描画（修正版1）

プログラムの修正2「座標軸とグラフのスケールを合わせる」

上記『関数のグラフの描画範囲を設定する』で、関数の定義域を$${-10 \leq x \leq 10}$$としてこの範囲がキャンバスの幅と一致するように設定しました。これを考慮すると、たとえば、点$${(-10,0)}$$はキャンバス上の$${(-\mathrm{width}/2,0)}$$にプロットされ、点$${(10,0)}$$はキャンバス上の$${(\mathrm{width}/2,0)}$$にプロットされることになるはずです。つまり、２次関数上の点$${(x,y)}$$をキャンバス上にプロットする場合は、そのままキャンバス上にプロットするのではなく、キャンバス上の座標に変換してからプロットする必要があります。この変換は、キャンバス上の座標を$${(X,Y)}$$とすると、

$$
X = \frac{\mathrm{width}}{2 \cdot 10} x, \ Y = \frac{\mathrm{height}}{2 \cdot 10} y
$$

で行うことができます（なお、分母の$${10}$$は関数の定義域$${-10 \leq x \leq 10}$$からきており、関数の定義域を$${-20 \leq x \leq 20}$$のように変更すると$${20}$$になります。）。図8で座標軸とグラフのスケールが一致していなかったのは、ソースコード8でこの変換が考慮されていなかったことが原因です。

では、この変換を考慮する形にソースコードを修正していきます。

// 関数のグラフを描く
void setup(){
  size(500, 500); // キャンバスの大きさを指定する
  translate(width/2, height/2); // 座標の中心をキャンバスの中心に移動する

  stroke(128,128,128); // 線の色をグレーにする
  
  // 軸の設定
  line(-width/2, 0.0, width/2, 0.0); // x軸
  line(0.0, -height/2, 0.0, height/2); // y軸
  
  // 目盛りの設定
  float scale_size = 10.0; // 目盛りの幅（pixel単位）
  int scale_num = 20; // 目盛りの数
  float pos_scale; // 目盛りの位置
  
  // x軸に目盛りを設定する
  for(int i=0; i<=scale_num; i++){
    pos_scale = -width/2.0 + i * width / scale_num;
    line(pos_scale, -scale_size/2.0, pos_scale, scale_size/2.0);
  }
  // y軸に目盛りを設定する
  for(int i=0; i<scale_num; i++){
    pos_scale = -height/2.0 + i * height / scale_num;
    line(-scale_size/2.0, pos_scale, scale_size/2.0, pos_scale);
  }

  float x_range = 10.0; // グラフの表示範囲を-x_rangeからx_rangeまでとする
  float y_range = 10.0; // グラフの表示範囲を-y_rangeからy_rangeまでとする

  // x軸とy軸の両端にxとyのそれぞれの範囲を表す数字を表示
  textAlign(LEFT, TOP);
  text("0", 0.0,0.0);
  textAlign(LEFT, TOP);
  text(int(-x_range), -width/2.0, 0.0);
  textAlign(RIGHT, TOP);
  text(int(x_range), width/2.0, 0.0);
  textAlign(LEFT, BOTTOM);
  text(int(-y_range), 0.0, height/2.0);
  textAlign(LEFT, TOP);
  text(int(y_range), 0.0, -height/2.0);
 
  scale(1,-1); // y軸正の向きを下向きから上向きに反転する

  noFill(); // グラフの中身を塗りつぶさない
  stroke(0,0,0); // グラフの線の色を黒色に設定

  // グラフの定義域
  float x_min = -x_range;
  float x_max = x_range;
  int plot_num = 200; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 頂点の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<=plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // 頂点のx座標
    y = quadraticfunction(x); // 頂点のy座標（関数の値）
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

}

// 2次関数
float quadraticfunction(
  float x
){
  return x*x + 4.0*x + 3.0;
}

ソースコード9　関数のグラフを描くプログラム（修正版2）

スケッチ「drawGraph」のテキストエディタ部分をソースコード9に書き換えて実行すると、図9のように、目標としていた座標軸とグラフ（図1）と同じものが描かれます。

図9　２次関数のグラフ（図1と同じもの）

なお、２次関数$${y=x^2+4x+3}$$は

$$
y=x^2+4x+3=(x+3)(x+1)
$$

と右辺を因数分解できますので、グラフは$${x}$$軸と$${(-3,0)}$$、$${(-1,0)}$$の２点で交わり、図9がそうなっていることがわかります。

まとめ

今回は、「高校数学をプログラミングで解く」で、今後実行ウィンドウのキャンバス上にグラフを描いていくための準備をしました。
プログラミング言語「Processing」には、グラフを描くためのツールなどは準備されていないようですので、座標軸などを自作して描き、その座標軸を利用してグラフを描きました。
初学者にはすこし難しく感じることもあるかもしれませんが、実際に自分で描きながら少しずつ理解していってください。

参考文献

Processingをはじめよう 第２版（オライリー・ジャパン、オーム社、ISBN9784873117737）