高校数学をプログラミングで解く（数学II編）「3-6 加法定理」

MK's papa

2024年2月24日 06:01

マガジンリスト　＞　数学Ⅱ編 3.三角関数　＞　3-6 加法定理

はじめに

今回は、数学IIで学ぶ「加法定理」について、加法定理を確かめるプログラムや２直線のなす角を求めるプログラムを作成します。

加法定理

まず、加法定理について解説しておきます。

加法定理

以下、複合同順とします。

$$
\sin (\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta
$$

$$
\cos (\alpha \pm \beta) = \cos \alpha \cos \beta \mp \sin \alpha \sin \beta
$$

$$
\tan (\alpha \pm \beta) = \frac{ \tan \alpha \pm \tan \beta }{1 \mp \tan \alpha \tan \beta }
$$

参考$${\sin(\alpha+\beta), \ \cos(\alpha+\beta), \ \tan(\alpha+\beta)}$$の公式で、$${\beta}$$を$${-\beta}$$とおくと、$${\sin(\alpha-\beta), \ \cos(\alpha-\beta), \ \tan(\alpha-\beta)}$$の公式が得られる。

２直線のなす角

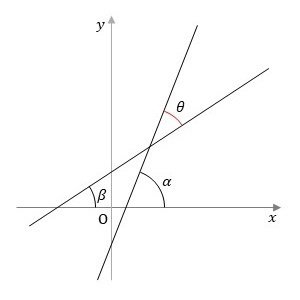
交わる２直線$${y=m_1x+n_1, \ y=m_2x+n_2}$$が垂直でないとき、そのなす鋭角を$${\theta, \ m_1=\tan \alpha, \ m_2=\tan \beta}$$とすると、

$$
\tan \theta = \left| \frac{ \tan \alpha - \tan \beta }{1 + \tan \alpha \tan \beta } \right| = \left| \frac{m_1-m_2}{1+m_1m_2} \right|
$$

加法定理を確かめる

今回、以下の問題で加法定理を用いた場合と用いない場合との三角関数の値を比較することで加法定理が成り立っていることを確かめるプログラムを作成します。

問題1
以下の値を加法定理を用いた場合と用いない場合とで求め、それらの値を比較せよ。
(1) $${ \sin 75^{\circ}, \ \sin 15^{\circ} }$$
(2) $${ \cos 75^{\circ}, \ \cos 15^{\circ} }$$
(3) $${ \tan 75^{\circ}, \ \tan 15^{\circ} }$$

アルゴリズム設計

問題1の角度$${75^{\circ}}$$と$${15^{\circ}}$$は、それぞれ$${75^{\circ}=45^{\circ}+30^{\circ}}$$と$${15^{\circ}=45^{\circ}-30^{\circ}}$$と分解できるので、
(1) $${\sin ( 45^{\circ} + 30^{\circ} ), \ \sin ( 45^{\circ} - 30^{\circ} )}$$
(2) $${\cos ( 45^{\circ} + 30^{\circ} ), \ \cos ( 45^{\circ} - 30^{\circ} )}$$
(3) $${\tan ( 45^{\circ} + 30^{\circ} ), \ \tan ( 45^{\circ} - 30^{\circ} )}$$
として、加法定理を用いた場合と用いない場合とで値を求めるようにします。

プログラム

では、加法定理を確かめるためのプログラムを作成します。

// 加法定理を確かめる問題
void setup(){

  // 2つの角度（ラジアン）
  float alpha = radians(45.0);
  float beta = radians(30.0);

  // (1) sin 75°,sin 15°
  float sin75_lhs = sin(alpha + beta);
  float sin75_rhs = addition_theorem_sin(alpha, beta);
  float sin15_lhs = sin(alpha - beta);
  float sin15_rhs = addition_theorem_sin(alpha, -beta);
  println("(1)sin 75°=", sin75_lhs, ",加法定理：", sin75_rhs);
  println("(1)sin 15°=", sin15_lhs, ",加法定理：", sin15_rhs);
  
  // (2) cos 75°,cos 15°
  float cos75_lhs = cos(alpha + beta);
  float cos75_rhs = addition_theorem_cos(alpha, beta);
  float cos15_lhs = cos(alpha - beta);
  float cos15_rhs = addition_theorem_cos(alpha, -beta);
  println("(2)cos 75°=", cos75_lhs, ",加法定理：", cos75_rhs);
  println("(2)cos 15°=", cos15_lhs, ",加法定理：", cos15_rhs);
  
  // (3) tan 75°,tan 15°
  float tan75_lhs = tan(alpha + beta);
  float tan75_rhs = addition_theorem_tan(alpha, beta);
  float tan15_lhs = tan(alpha - beta);
  float tan15_rhs = addition_theorem_tan(alpha, -beta);
  println("(3)tan 75°=", tan75_lhs, ",加法定理：", tan75_rhs);
  println("(3)tan 15°=", tan15_lhs, ",加法定理：", tan15_rhs);

}

// sin(α+β)の公式
float addition_theorem_sin(
  float alpha, // 1つ目の角度（ラジアン）
  float beta   // 2つ目の角度（ラジアン）
){
  return sin(alpha)*cos(beta)+cos(alpha)*sin(beta);
}

// cos(α+β)の公式
float addition_theorem_cos(
  float alpha, // 1つ目の角度（ラジアン）
  float beta   // 2つ目の角度（ラジアン）
){
  return cos(alpha)*cos(beta)-sin(alpha)*sin(beta);
}

// tan(α+β)の公式
float addition_theorem_tan(
  float alpha, // 1つ目の角度（ラジアン）
  float beta   // 2つ目の角度（ラジアン）
){
  return (tan(alpha)+tan(beta))/(1.0-tan(alpha)*tan(beta));
}

ソースコード1　加法定理を確かめるプログラム

ソースコード1では、$${\sin (\alpha+\beta), \ \cos (\alpha+\beta), \ \tan (\alpha+\beta) }$$に対する加法定理の公式をそれぞれaddition_theorem_sin、addition_theorem_cos、addition_theorem_tan 関数として定義しています。なお、$${\sin (\alpha-\beta), \ \cos (\alpha-\beta), \ \tan (\alpha-\beta) }$$に対する加法定理は準備せず、上記「加法定理」の「参考」で説明したしたように、$${\beta}$$を$${-\beta}$$とすることでaddition_theorem_sin、addition_theorem_cos、addition_theorem_tan 関数を用いて計算するようにしています。

ソースコード1を、Processingの開発環境ウィンドウを開いて（スケッチ名を「check_addition_theorem」としています）、テキストエディタ部分に書いて実行します。

図2のように、コンソールにそれぞれの問題に対して加法定理を用いない場合と用いる場合との結果が出力されます。

(1)sin 75°= 0.9659258 ,加法定理： 0.9659258
(1)sin 15°= 0.25881904 ,加法定理： 0.258819
(2)cos 75°= 0.25881907 ,加法定理： 0.258819
(2)cos 15°= 0.9659258 ,加法定理： 0.9659258
(3)tan 75°= 3.7320504 ,加法定理： 3.7320507
(3)tan 15°= 0.2679492 ,加法定理： 0.2679492

これらの結果を見ると、加法定理を用いない場合と用いる場合とでそれぞれの値は丸め誤差の範囲内で一致していることがわかります。なお、問題1の場合、

$$
\sin 45^{\circ} = \frac{1}{\sqrt{2}}, \ \cos 45^{\circ} = \frac{1}{\sqrt{2}}, \ \tan 45^{\circ} = 1
$$

$$
\sin 30^{\circ} = \frac{1}{2}, \ \cos 30^{\circ} = \frac{\sqrt{3}}{2}, \ \tan 30^{\circ} = \frac{1}{\sqrt{3}}
$$

がわかっているので、加法定理を用いると、

$$
\sin 75^{\circ} = \frac{\sqrt{6}+\sqrt{2}}{4}, \ \sin 15^{\circ} = \frac{\sqrt{6}-\sqrt{2}}{4}
$$

$$
\cos 75^{\circ} = \frac{\sqrt{6}-\sqrt{2}}{4}, \ \cos 15^{\circ} = \frac{\sqrt{6}+\sqrt{2}}{4}
$$

$$
\tan 75^{\circ} = 2+\sqrt{3}, \ \tan 15^{\circ} = 2-\sqrt{3}
$$

となります。

２直線のなす角を求める

次に、２直線のなす角を求めるプログラムを作成します。

問題2
次の２直線のなす角$${\theta}$$を求めよ。ただし、$${0 < \theta < \pi/2}$$とする。
(1) $${ y = \frac{3}{2}x, \ y=-5x }$$
(2) $${ y = 2x, y=-3x+2 }$$

アルゴリズム設計

この問題2は、２直線のなす角を求める公式を用いるだけですので、比較的簡単に計算することができます。公式の部分は関数化しておきます。

プログラム

では、２直線のなす角を求めるプログラムを作成します。

// ２直線のなす角を求める
void setup(){

  // ２直線の傾きと切片
  float m1, n1, m2, n2;
  
  // (1) 
  m1 = 3.0/2.0;
  n1 = 0.0;
  m2 = -5.0;
  n2 = 0.0;
  float theta1 = calc_formed_angle(m1,m2);
  println("(1):", theta1 + "°");
  
  // (2) 
  m1 = 2.0;
  n1 = 0.0;
  m2 = -3.0;
  n2 = 2.0;
  float theta2 = calc_formed_angle(m1,m2);
  println("(2):", theta2 + "°");
  
}

// ２直線のなす角を求める関数
float calc_formed_angle(
  float m1, // 1つ目の直線の傾き
  float m2  // 2つ目の直線の傾き
){
  float t = abs( (m1-m2)/(1.0+m1*m2) ); // tan θ
  float theta = atan(t); // なす角θ 
  return degrees(theta);
}

ソースコード2　２直線のなす角を求めるプログラム

なお、ソースコード2では、２直線のなす角を求める関数 calc_formed_angle の返り値を弧度法（ラジアン）ではなく、度数法（°）で出力するようにしています。

ソースコード2を、Processingの開発環境ウィンドウを開いて（スケッチ名を「calc_formed_angles」としています）、テキストエディタ部分に書いて実行します。

図3のように、コンソールに問題2のそれぞれのなす角の値が出力されます。

(1): 45.0°
(2): 45.0°

おまけ（宿題）

問題2の結果を図1のように図示するプログラムを作成することは勉強になると思いますので、是非チャレンジしてみてください。なお、図1のように$${\alpha, \beta, \theta}$$などの文字を描画する必要はないです。座標軸や直線、およびなす角を描画してみてください。
以下に、このプログラムを作成する際のヒントを示しておきます。
① ベースとなるスケッチは、記事『高校数学をプログラミングで解く（数学II編）「2-1 直線の方程式」』で作成したスケッチ「drawEquationOfLine1」を再利用した方が便利です。なお、「draw_equation_of_line1」関数は、直線の方程式の一般形$${ax+by+c=0}$$をベースにしていますが、この問題2に対してはもう一つの一般形$${y=mx+n}$$によるものに修正して利用する方がよいでしょう。
② ２直線のなす角は扇形で描きます。これを行うために arc 関数を利用します。２直線が交わる点を$${(x,y)}$$とし、また２直線の傾きを$${m_1 = \tan \alpha, m_2 = \tan \beta}$$で表すと、

noFill();
arc(x,y,r,r,alpha,beta,OPEN);

で描くことができます。変数 r は扇形のベースとなる円の直径を表し、図形のサイズに合わせて調整します。
③ なす角は$${0 < \theta < \pi/2}$$ですので、なす角を描く際にはもう一工夫必要になります。これについてはちょっと考えてみてください。

まとめ

今回は、数学IIで学ぶ「加法定理」について、加法定理を確かめるプログラムや２直線のなす角を求めるプログラムを作成しました。
加法定理は三角関数を扱う上で基本的で重要な公式となります。特に、$${\sin (\alpha \pm \beta), \ \cos (\alpha \pm \beta)}$$の公式だけは覚えておきましょう。なぜなら、その他の三角関数の公式のほとんどがこれら$${\sin (\alpha \pm \beta), \ \cos (\alpha \pm \beta)}$$の公式から導くことができるからです。
また、２直線のなす角を求める公式を用いると、なす角はすぐに求めることができますが、このなす角を図示してみることはこの公式の意味を理解する上で有用になるでしょう。ぜひ上記ヒントをもとに描いてみてください。そして、問題2以外のいろいろな２直線についてもチャレンジしてみてください。

参考文献

改訂版教科書傍用スタンダード数学II（数研出版、ISBN9784410209369）

この記事が気に入ったらサポートをしてみませんか？