高校数学をプログラミングで解く（数学III編）「2-4 ２次曲線の移動」

割引あり

MK's papa

2024年9月18日 04:16

マガジンリスト　＞　数学Ⅲ編 2.式と曲線　＞　2-4 ２次曲線の移動

はじめに

今回は、数学IIIで学ぶ「２次曲線の移動」について、平行移動や回転移動を用いて任意の２次曲線を描くプログラムを作成します。

２次曲線の移動

まず、２次曲線の移動について解説します。

平行移動

曲線$${F(x,y)=0}$$を$${x}$$軸方向に$${p}$$、$${y}$$軸方向に$${q}$$だけ平行移動して得られる曲線の方程式は

$$
F(x-p, y-q)=0
$$

対称移動

曲線$${F(x,y)=0}$$を直線や原点に関して対称移動して得られる曲線の方程式は、次のようになる。
① $${x}$$軸　　　　$${F(x,-y)=0}$$
② $${y}$$軸　　　　$${F(-x,y)=0}$$
③ 直線$${y=x}$$　$${F(y,x)=0}$$
④ 原点　　　　$${F(-x,-y)=0}$$

回転移動

曲線$${F(x,y)=0}$$を原点を中心として$${\theta}$$だけ回転移動して得られる曲線の方程式は

$$
F(x \cos \theta + y \sin \theta, -x \sin \theta + y \cos \theta) = 0
$$

※回転移動についてはもう少し補足しておきます。

回転移動して得られる曲線の方程式を求める場合
① 回転移動後の曲線を$${xy}$$座標系上に描きます（図1）。

② この回転移動後の曲線を$${x}$$軸上に焦点があるようなわかりやすい曲線になるように、新たに$${x'y'}$$座標系を設定します（図2）。

このように$${x'y'}$$座標系を設定すると、例えば、放物線は

$$
y'^2 = 4 p x' \ \ (p > 0) \ \ \ \ \Rightarrow \ \ \ \ F(x',y') = y'^2-4px' = 0
$$

と$${x'}$$軸を軸とする放物線となり、楕円は

$$
\frac{x'^2}{a^2} +\frac{y'^2}{b^2} = 1 \ \ (a > b > 0) \ \ \ \ \Rightarrow \ \ \ \ F(x',y') = \frac{x'^2}{a^2} +\frac{y'^2}{b^2} -1 = 0
$$

と焦点が$${x'}$$軸上にある楕円となり、双曲線は

$$
\frac{x'^2}{a^2} -\frac{y'^2}{b^2} = 1 \ \ (a >0, b > 0) \ \ \ \ \Rightarrow \ \ \ \ F(x',y') = \frac{x'^2}{a^2} -\frac{y'^2}{b^2} -1 = 0
$$

と、焦点が$${x'}$$軸上にある双曲線となります。

③ $${xy}$$座標系と$${x'y'}$$座標系との関係を見ていきます。
$${x}$$軸の正の向きを基準として$${x'}$$軸の正の向きの角度を$${\theta}$$とします。それから２次曲線上の任意の点を$${\mathrm{P}}$$とし、座標系の原点$${\mathrm{O}}$$から点$${\mathrm{P}}$$までの距離を$${r}$$、$${x'}$$軸の正の向きを基準として線分$${\mathrm{OP}}$$の角度を$${\varphi}$$とします（図3）。

点$${\mathrm{P}}$$を$${xy}$$座標系でみたときの座標を$${(x,y)}$$とし、$${x'y'}$$座標系でみたときの座標を$${(x',y')}$$として、これらを極座標系で表すと、

$$
x = r \cos (\varphi + \theta), \ \ y = r \sin (\varphi + \theta) \\
x' = r \cos \varphi, \ \ y' = r \sin \varphi
$$

となります。したがって、加法定理を用いると、

$$
x = r \cos \varphi \cos \theta - r \sin \varphi \sin \theta = x' \cos \theta - y' \sin \theta \\
y = r \cos \varphi \sin \theta + r \sin \varphi \cos \theta = x' \sin \theta + y' \cos \theta
$$

が得られます。これらの式を変形して、$${(x',y')}$$を$${(x,y)}$$で表すと、

$$
x' = x \cos \theta + y \sin \theta \\
y' = -x \sin \theta + y \cos \theta
$$

となります。

④ 最後に、上記の式を$${F(x',y')=0}$$の式に代入すると、曲線$${F(x,y)=0}$$を原点を中心として$${\theta}$$だけ回転移動して得られる曲線の方程式は

$$
F(x \cos \theta + y \sin \theta, -x \sin \theta + y \cos \theta) = 0
$$

と得られます。

曲線を回転する場合
① 曲線$${F(x,y)=0}$$（図4の青色の曲線）を原点回りに$${\theta}$$だけ回転させること（図4の赤色の曲線）を考えます。

② このとき、曲線$${F(x,y)=0}$$上の任意の点を$${\mathrm{P}(x,y)}$$とし、点$${\mathrm{P}}$$を原点回りに$${\theta}$$だけ回転した点を$${\mathrm{Q}(x',y')}$$とします（図5）。

③ そして、座標系の原点$${\mathrm{O}}$$から点$${\mathrm{P}}$$までの距離を$${r}$$、$${x}$$軸の正の向きを基準として線分$${\mathrm{OP}}$$の角度を$${\varphi}$$とします。このとき、点$${\mathrm{P}(x,y)}$$を極座標で表すと、

$$
x = r \cos \varphi, \ \ y = r \sin \varphi
$$

となります。一方、点$${\mathrm{Q}(x',y')}$$を極座標で表すと、

$$
x' = r \cos ( \varphi + \theta ), \ \ y' = r \sin ( \varphi + \theta )
$$

となります。したがって、加法定理を用いると、

$$
x' = r \cos \varphi \cos \theta - r \sin \varphi \sin \theta = x \cos \theta - y \sin \theta, \\
y' = r \cos \varphi \sin \theta + r \sin \varphi \cos \theta = x \sin \theta + y \cos \theta
$$

となります。
④ 以上のことから、曲線$${F(x,y)=0}$$を原点回りに$${\theta}$$だけ回転移動させるには、曲線上の点$${(x,y)}$$を

$$
x' = x \cos \theta - y \sin \theta, \\
y' = x \sin \theta + y \cos \theta
$$

の座標変換によって得られる点$${(x',y')}$$に移動させることで実現できます。

任意の２次曲線を描く

２次曲線の移動方法がわかったので、プログラムで任意の２次曲線を描くための準備をしていきます。

任意の放物線を描く

まず、任意の放物線を描くためのアルゴリズムを考えていきます。基本的な考え方として、$${x}$$軸を軸とする放物線$${y^2=4\alpha x \ (\alpha \neq 0)}$$を平行移動、回転移動して任意の放物線を描くようにします。
描きたい放物線の焦点を$${\mathrm{F}(x_1,y_1)}$$、準線を直線$${l \ : \ ax+by+c=0}$$とします。
① 焦点$${\mathrm{F}}$$から準線$${l}$$に下した垂線が交わる点$${\mathrm{H}(x_2, y_2)}$$を求めます。

$$
x_2 = \frac{b^2x_1-aby_1-ac}{a^2+b^2}, \ \ y_2 = \frac{-abx_1+a^2y_1-bc}{a^2+b^2}
$$

となります。
② 焦点$${\mathrm{F}}$$と$${\mathrm{H}}$$との距離$${d}$$、$${\mathrm{F}}$$と$${\mathrm{H}}$$との中点$${\mathrm{C}(p,q)}$$を求めます。

$$
d = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2}, \ \ p = \frac{x_1+x_2}{2}, \ \ q = \frac{y_1+y_2}{2}
$$

このとき、放物線$${y^2=4\alpha x}$$の$${\alpha}$$の値は、

$$
\alpha = \frac{d}{2}
$$

となります。

③ ベクトル$${\overrightarrow{\mathrm{HF}}}$$と$${x}$$軸の正の方向との間の角度$${\theta}$$を求めます。

$$
\tan \theta = \frac{y_1-y_2}{x_1-x_2}
$$

④ ①②③の結果を利用すると、焦点$${\mathrm{F}(x_1,y_1)}$$、準線$${l \ : \ ax+by+c=0}$$とする放物線は、$${x}$$軸を軸とする放物線$${y^2=4\alpha x}$$を原点を中心として$${\theta}$$だけ回転移動した後、$${x}$$軸方向に$${p}$$、$${y}$$軸方向に$${q}$$だけ平行移動することによって得られます。

任意の楕円を描く

任意の楕円を描くためのアルゴリズムを考えていきます。基本的な考え方として、中心が原点で、焦点が$${x}$$軸上にある楕円

$$
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \ \ (a > b > 0)
$$

を平行移動、回転移動して任意の楕円を描くようにします。
描きたい楕円の２つの焦点を$${\mathrm{F}(x_1,y_1)}$$、$${\mathrm{F'}(x_2,y_2)}$$、楕円上の点から２つの焦点までの距離の和を$${r}$$とします。
① ２つの焦点$${\mathrm{F}}$$と$${\mathrm{F'}}$$との距離$${d}$$、$${\mathrm{F}}$$と$${\mathrm{F'}}$$との中点$${\mathrm{C}(p,q)}$$を求めます。

$$
d = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2}, \ \ p = \frac{x_1+x_2}{2}, \ \ q = \frac{y_1+y_2}{2}
$$

② ベクトル$${\overrightarrow{\mathrm{F'F}}}$$と$${x}$$軸の正の方向との間の角度$${\theta}$$を求めます。

$$
\tan \theta = \frac{y_1-y_2}{x_1-x_2}
$$

③ 楕円上の点から２つの焦点までの距離の和$${r}$$は楕円の長軸の長さ$${2a}$$と同じであることから、

$$
a = \frac{r}{2}
$$

となります。

④ 楕円の２つの焦点間の距離$${d}$$は、楕円の長軸の長さ$${2a}$$、短軸の長さ$${2b}$$で表すと、

$$
d = 2 \sqrt{a^2-b^2}
$$

となるので、

$$
b = \frac{\sqrt{r^2-d^2}}{2}
$$

となります。

⑤ ①②③④の結果を利用すると、２つの焦点$${\mathrm{F}(x_1,y_1)}$$、$${\mathrm{F'}(x_2,y_2)}$$をもち、楕円上の点から２つの焦点までの距離の和が$${r}$$となる楕円は、中心が原点で２つの焦点が$${x}$$軸上にある楕円

$$
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
$$

を、原点を中心として$${\theta}$$だけ回転移動した後、$${x}$$軸方向に$${p}$$、$${y}$$軸方向に$${q}$$だけ平行移動することによって得られます。

任意の双曲線を描く

任意の双曲線を描くためのアルゴリズムを考えていきます。基本的な考え方として、中心が原点で、焦点が$${x}$$軸上にある双曲線

$$
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1
$$

を平行移動、回転移動して任意の双曲線を描くようにします。
描きたい双曲線の２つの焦点を$${\mathrm{F}(x_1,y_1)}$$、$${\mathrm{F'}(x_2,y_2)}$$、双曲線上の点から２つの焦点までの距離の差を$${r}$$とします。
① ２つの焦点$${\mathrm{F}}$$と$${\mathrm{F'}}$$との距離$${d}$$、$${\mathrm{F}}$$と$${\mathrm{F'}}$$との中点$${\mathrm{C}(p,q)}$$を求めます。

$$
d = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2}, \ \ p = \frac{x_1+x_2}{2}, \ \ q = \frac{y_1+y_2}{2}
$$

② ベクトル$${\overrightarrow{\mathrm{F'F}}}$$と$${x}$$軸の正の方向との間の角度$${\theta}$$を求めます。

$$
\tan \theta = \frac{y_1-y_2}{x_1-x_2}
$$

③ 双曲線上の点から２つの焦点までの距離の差$${r}$$は双曲線の２つの頂点間の距離$${2a}$$と同じであることから、

$$
a = \frac{r}{2}
$$

となります。

④ 双曲線の２つの焦点間の距離$${d}$$は、双曲線のパラメータ$${a,b}$$で表すと、

$$
d = 2 \sqrt{a^2+b^2}
$$

となるので、

$$
b = \frac{\sqrt{d^2-r^2}}{2}
$$

となります。

⑤ ①②③④の結果を利用すると、２つの焦点$${\mathrm{F}(x_1,y_1)}$$、$${\mathrm{F'}(x_2,y_2)}$$をもち、双曲線上の点から２つの焦点までの距離の差が$${r}$$となる双曲線は、中心が原点で２つの焦点が$${x}$$軸上にある双曲線

$$
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1
$$

を、原点を中心として$${\theta}$$だけ回転移動した後、$${x}$$軸方向に$${p}$$、$${y}$$軸方向に$${q}$$だけ平行移動することによって得られます。

任意の放物線を描くプログラム

次の問題を例に、任意の放物線を描くプログラムを作成します。

問題1
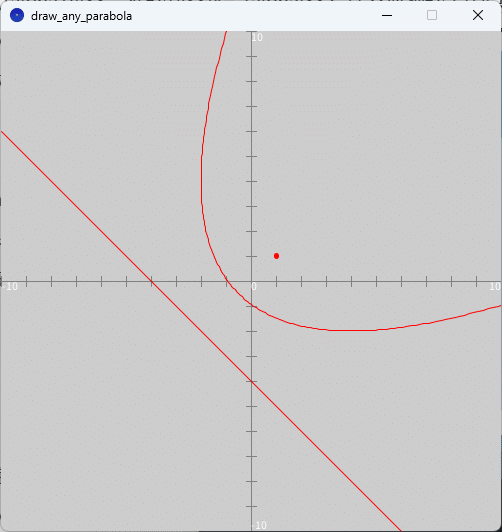
焦点$${(1,1)}$$、準線$${x+y+4=0}$$とする放物線の軌跡を描け。

グラフを描くので、記事『高校数学をプログラミングで解く（数学I編）「1-0-2 グラフを描くための準備（その2）」』で準備した座標軸を描く関数 setAxes を利用します。以下の zip ファイルをダウンロードして展開または解凍してください。

そして、スケッチの名前（フォルダ名）を「draw_any_parabola」と変更し、またスケッチ「draw_any_parabola」内の「drawFunction.pde」ファイルの名前を「draw_any_parabola.pde」に変更します。そして、pdeファイル「draw_any_parabola.pde」をダブルクリックしてスケッチ「draw_any_parabola」の開発環境ウィンドウを立ち上げます。そして、開発環境ウィンドウのタブ欄で「draw_any_parabola」タブを選択して、そのテキストエリアのソースコードを以下のソースコード1に書き換えます。

float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500);
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  
  noFill();
  stroke(0,0,0);
  
  // 焦点(1,1),準線x+y+4=0の放物線 
  float x1 = 1.0; // 焦点のx座標
  float y1 = 1.0; // 焦点のy座標
  float a = 1.0; // 準線のxの係数
  float b = 1.0; // 準線のyの係数
  float c = 4.0; // 準線の定数項
  stroke(255,0,0);
  draw_parabola(x1,y1,a,b,c);
}

// 焦点(x1,y1)、準線ax+by+c=0とする放物線を描く関数
void draw_parabola(
  float x1, // 焦点のx座標
  float y1, // 焦点のy座標
  float a, // 準線のxの係数
  float b, // 準線のyの係数
  float c  // 準線の定数項
){
  // グラフの定義域
  float y_min = -y_range;
  float y_max = y_range;
  int plot_num = 200; // グラフを描くための頂点の個数  
  
  // 焦点から準線に下した垂線が交わる点(x2,y2)
  float x2 = (b*b*x1-a*b*y1-a*c)/(a*a+b*b);
  float y2 = (-a*b*x1+a*a*y1-b*c)/(a*a+b*b);

  // 焦点と垂線が交わる点との距離d
  float d = sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));

  // 焦点と垂線が交わる点との中点（p,q)
  float p = (x1+x2)/2.0;
  float q = (y1+y2)/2.0;

  // x軸を軸とする放物線のパラメータ
  float alpha = d/2.0;
  
  // x軸を軸とする放物線を回転させる角度
  float theta = atan2(y1-y2,x1-x2);

  // グラフを描画
  float xp, yp; // x軸を軸とする放物線上の点の座標
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<=plot_num; i++){
    yp = y_min + (y_max - y_min) / plot_num * i; // x軸を軸とする放物線上の点のy座標
    xp = yp*yp/4.0/alpha; // x軸を軸とする放物線上の点のx座標

    // 回転移動、平行移動
    x = xp * cos(theta) - yp * sin(theta) + p;
    y = xp * sin(theta) + yp * cos(theta) + q;

    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();
  
  // 焦点をプロット
  plot_point(x1,y1);
  
  // 準線を描く
  float x_l = -x_range;
  float y_l = -a*x_l/b - c/b;
  float x_r = x_range;
  float y_r = -a*x_r/b - c/b;
  float X_l = width / 2.0 / x_range * x_l;
  float Y_l = height / 2.0 / y_range * y_l;
  float X_r = width / 2.0 / x_range * x_r;
  float Y_r = height / 2.0 / y_range * y_r;
  line(X_l,Y_l, X_r, Y_r);
  
}  

// 座標(x,y)に点をプロットする関数
void plot_point(
  float x, // 点のx座標
  float y  // 点のy座標
){
  float X, Y; // キャンバス上の座標
  // キャンバス上の座標位置に換算
  X = width / 2.0 / x_range * x;
  Y = height / 2.0 / y_range * y;
  strokeWeight(5);
  point(X, Y);
  strokeWeight(1);
}

ソースコード1　任意の放物線を描くプログラム

ソースコード1では、焦点$${(x_1,y_1)}$$、準線$${ax+by+c=0}$$とする放物線を描く関数 draw_parabola を準備し、この draw_parabola 関数を setup 関数内で呼び出すことで放物線を描きます。また、 draw_parabola 関数では、焦点が$${(\alpha,0)}$$、準線が$${x=-\alpha}$$となる放物線上の点を、原点回りに$${\theta}$$だけ回転移動し、$${x}$$軸方向に$${p}$$、$${y}$$軸方向に$${q}$$だけ平行移動したあと、プロットすることで任意の放物線を描くようにしています。

「draw_any_parabola」タブのテキストエリアをソースコード1に書き換えて、スケッチ「draw_any_parabola」を実行すると、図6のように、実行ウィンドウのキャンバス上に問題1の放物線が赤色で描かれます。

任意の楕円を描くプログラム

今度は次の問題を例に、任意の楕円を描くプログラムを作成します。

問題2
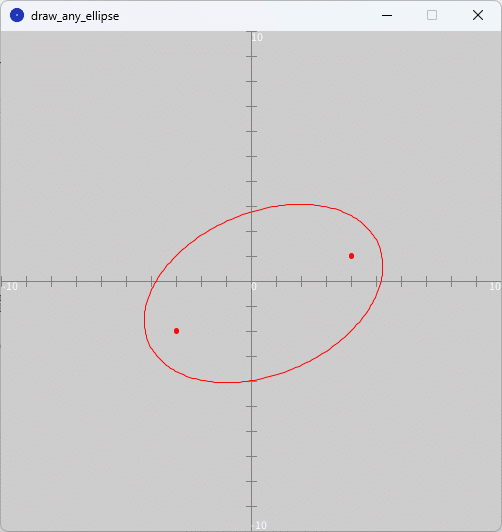
2定点$${(4,1), (-3,-2)}$$までの距離の和が$${10}$$となる楕円の軌跡を描け。

先程作成したスケッチ「draw_any_parabola」を再利用します。
スケッチ「draw_any_parabola」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「draw_any_ellipse」と変更し、またスケッチ「draw_any_ellipse」内の「draw_any_parabola.pde」ファイルの名前を「draw_any_ellipse.pde」に変更します。そして、pdeファイル「draw_any_ellipse.pde」をダブルクリックしてスケッチ「draw_any_ellipse」の開発環境ウィンドウを立ち上げます。そして、開発環境ウィンドウのタブ欄で「draw_any_ellipse」タブを選択して、そのテキストエリアのソースコードを以下のソースコード2に書き換えます。

float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500);
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  
  noFill();
  stroke(0,0,0);
  
  // 2定点(4,1),(-3,-2)までの距離の和が10となる楕円
  float x1 = 4.0; // 焦点1のx座標
  float y1 = 1.0; // 焦点1のy座標
  float x2 = -3.0; // 焦点2のx座標
  float y2 = -2.0; // 焦点2のy座標
  float r = 10.0; // 距離の和
  stroke(255,0,0);
  draw_ellipse(x1,y1,x2,y2,r);

}

// 焦点(x1,y1),(x2,y2)からの距離の和がrとなる楕円を描く関数
void draw_ellipse(
  float x1, // 焦点1のx座標
  float y1, // 焦点1のy座標
  float x2, // 焦点2のx座標
  float y2, // 焦点2のy座標
  float r   // 距離の和
){
  
  // ２つの焦点間の距離d
  float d = sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));

  // ２つの焦点間の中点（p,q)
  float p = (x1+x2)/2.0;
  float q = (y1+y2)/2.0;

  // ２つの焦点がx軸上にある楕円のパラメータ
  float a = r/2.0;
  float b = sqrt(r*r-d*d)/2.0;
  
  // ２つの焦点がx軸上にある楕円を回転させる角度
  float theta = atan2(y1-y2,x1-x2);

  // グラフを描画
  int plot_num = 200; // グラフを描くための頂点の個数  
  
  float xp, yp; // 2つの焦点がx軸上にある楕円上の点の座標
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<=plot_num; i++){
    xp = a * cos(2.0 * PI / plot_num * i); // 2つの焦点がx軸上にある楕円上の点のx座標
    yp = b * sin(2.0 * PI / plot_num * i); // 2つの焦点がx軸上にある楕円上の点のy座標

    // 回転移動、平行移動
    x = xp * cos(theta) - yp * sin(theta) + p;
    y = xp * sin(theta) + yp * cos(theta) + q;

    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();
  
  // 焦点をプロット
  plot_point(x1,y1);
  plot_point(x2,y2);  
}  

// 座標(x,y)に点をプロットする関数
void plot_point(
  float x, // 点のx座標
  float y  // 点のy座標
){
  float X, Y; // キャンバス上の座標
  // キャンバス上の座標位置に換算
  X = width / 2.0 / x_range * x;
  Y = height / 2.0 / y_range * y;
  strokeWeight(5);
  point(X, Y);
  strokeWeight(1);
}

ソースコード2　任意の楕円を描くプログラム

ソースコード2では、焦点$${(x_1,y_1),(x_2,y_2)}$$からの距離の和が$${r}$$となる楕円を描く関数 draw_ellipse を準備し、この draw_ellipse 関数を setup 関数内で呼び出すことで楕円を描きます。なお、記事『高校数学をプログラミングで解く（数学III編）「2-2 楕円」』では、Processingで用意されている楕円を描く関数 ellipse を利用しましたが、今回の draw_parabola 関数では、ellipse 関数を利用せず、焦点$${(\sqrt{a^2-b^2},0),(-\sqrt{a^2-b^2},0) }$$からの距離の和が$${2a}$$となる楕円上の点$${(x,y)}$$をパラメータ表示

$$
x = a \cos \theta, y = b \sin \theta
$$

で表し、$${\theta}$$を$${0}$$から$${2\pi}$$まで動かすことで楕円上の点を求め、その点を原点回りに$${\theta}$$だけ回転移動し、$${x}$$軸方向に$${p}$$、$${y}$$軸方向に$${q}$$だけ平行移動したあと、プロットすることで任意の楕円を描くようにしています。

「draw_any_ellipse」タブのテキストエリアをソースコード2に書き換えて、スケッチ「draw_any_ellipse」を実行すると、図7のように、実行ウィンドウのキャンバス上に問題2の楕円が赤色で描かれます。

任意の双曲線を描くプログラム

最後に次の問題を例に、任意の双曲線を描くプログラムを作成します。

問題3
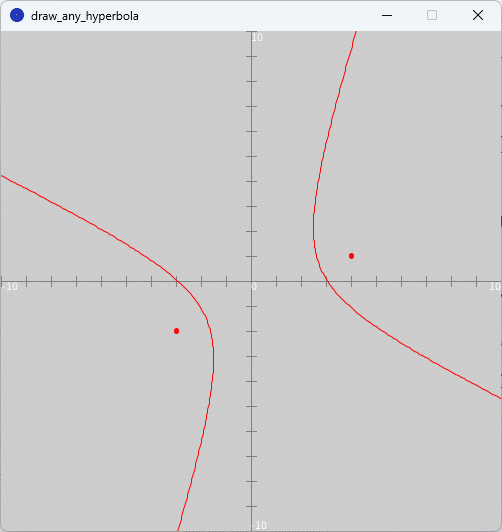
2定点$${(4,1), (-3,-2)}$$までの距離の差が$${5}$$となる双曲線の軌跡を描け。

こちらも、先程作成したスケッチ「draw_any_parabola」を再利用します。
スケッチ「draw_any_parabola」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「draw_any_hyperbola」と変更し、またスケッチ「draw_any_hyperbola」内の「draw_any_parabola.pde」ファイルの名前を「draw_any_hyperbola.pde」に変更します。そして、pdeファイル「draw_any_hyperbola.pde」をダブルクリックしてスケッチ「draw_any_hyperbola」の開発環境ウィンドウを立ち上げます。そして、開発環境ウィンドウのタブ欄で「draw_any_hyperbola」タブを選択して、そのテキストエリアのソースコードを以下のソースコード3に書き換えます。

float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500);
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  
  noFill();
  stroke(0,0,0);
  
  // 焦点(4,1),(-3,-2)からの距離の差が5となる双曲線を描く関数
  float x1 = 4.0; // 焦点1のx座標
  float y1 = 1.0; // 焦点1のy座標
  float x2 = -3.0; // 焦点2のx座標
  float y2 = -2.0; // 焦点2のy座標
  float r = 5.0; // 距離の差
  stroke(255,0,0);
  draw_hyperbola(x1,y1,x2,y2,r);

}

// 焦点(x1,y1),(x2,y2)からの距離の差がrとなる双曲線を描く関数
void draw_hyperbola(
  float x1, // 焦点1のx座標
  float y1, // 焦点1のy座標
  float x2, // 焦点2のx座標
  float y2, // 焦点2のy座標
  float r   // 距離の和
){
  // 2つの焦点間の距離d
  float d = sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));

  // ２つの焦点間の中点（p,q)
  float p = (x1+x2)/2.0;
  float q = (y1+y2)/2.0;

  // 2つの焦点がx軸上にある楕円のパラメータ
  float a = r/2.0;
  float b = sqrt(d*d-r*r)/2.0;
  
  // x軸を軸とする放物線を回転させる角度
  float theta = atan2(y1-y2,x1-x2);

  // グラフを描画
  float y_min = -y_range;
  float y_max = y_range;
  int plot_num = 200; // グラフを描くための頂点の個数 
  
  float xp, yp; // x軸を軸とする放物線上の点の座標
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<=plot_num; i++){
    yp = y_min + (y_max - y_min) / plot_num * i; // 2つの焦点がx軸上にある双曲線上の点のy座標
    xp = a * sqrt(1.0 + yp*yp/b/b); // 2つの焦点がx軸上にある双曲線上の点のx座標

    // 回転移動、平行移動
    x = xp * cos(theta) - yp * sin(theta) + p;
    y = xp * sin(theta) + yp * cos(theta) + q;

    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();
  // もう一方も描く
  beginShape();
  for(int i=0; i<=plot_num; i++){
    yp = y_min + (y_max - y_min) / plot_num * i; // 2つの焦点がx軸上にある双曲線上の点のy座標
    xp = -a * sqrt(1.0 + yp*yp/b/b); // 2つの焦点がx軸上にある双曲線上の点のx座標

    // 回転移動、平行移動
    x = xp * cos(theta) - yp * sin(theta) + p;
    y = xp * sin(theta) + yp * cos(theta) + q;

    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();
  
  // 焦点をプロット
  plot_point(x1,y1);
  plot_point(x2,y2);
}  

// 座標(x,y)に点をプロットする関数
void plot_point(
  float x, // 点のx座標
  float y  // 点のy座標
){
  float X, Y; // キャンバス上の座標
  // キャンバス上の座標位置に換算
  X = width / 2.0 / x_range * x;
  Y = height / 2.0 / y_range * y;
  strokeWeight(5);
  point(X, Y);
  strokeWeight(1);
}

ソースコード3　任意の双曲線を描くプログラム

ソースコード3では、焦点$${(x_1,y_1),(x_2,y_2)}$$からの距離の差が$${r}$$となる双曲線を描く関数 draw_hyperbola を準備し、この draw_hyperbola 関数を setup 関数内で呼び出すことで双曲線を描きます。また、 draw_hyperbola 関数では、焦点$${(\sqrt{a^2+b^2},0),(-\sqrt{a^2+b^2},0) }$$からの距離の差が$${2a}$$となる双曲線上の点を、原点回りに$${\theta}$$だけ回転移動し、$${x}$$軸方向に$${p}$$、$${y}$$軸方向に$${q}$$だけ平行移動したあと、プロットすることで任意の双曲線を描くようにしています。

「draw_any_hyperbola」タブのテキストエリアをソースコード3に書き換えて、スケッチ「draw_any_hyperbola」を実行すると、図8のように、実行ウィンドウのキャンバス上に問題3の双曲線が赤色で描かれます。

まとめ

今回は、数学IIIで学ぶ「２次曲線の移動」について、平行移動や回転移動を用いて任意の2次曲線を描くプログラムを作成しました。
今回作成したプログラムでは、まず中心が座標の原点で$${x}$$軸上に焦点があるような２次曲線を考え、その曲線上に乗っている点を回転移動や平行移動して、プロットしていくことで任意の２次曲線を描いていきました。
なお、回転移動については、回転移動して得られる曲線の方程式を求める場合と曲線を回転する場合とで回転方向を考える際に少し注意が必要です。これについて回転移動の解説を読んで頭の中を整理しておくことをお勧めします。

参考文献

改訂版教科書傍用スタンダード・オリジナル数学III（数研出版、ISBN9784410209567）

演習問題

次の方程式が表す軌跡を描くプログラムを作成してください。
(1) $${y^2+4y-4x+12=0}$$
(2) $${9x^2+4y^2-36x+8y+4=0}$$
(3) $${x^2 -4y^2+4x+24y-36=0}$$

演習問題の解答例

ここから先は

934字 / 1画像 / 1ファイル

ログイン

この記事が気に入ったらサポートをしてみませんか？