高校数学をプログラミングで解く(数学III編)「2-2 楕円」
マガジンリスト > 数学Ⅲ編 2.式と曲線 > 2-2 楕円
はじめに
今回は、数学IIIで学ぶ「楕円」について、楕円を描くプログラムを作成します。
楕円
まず、楕円について解説します。
定義
異なる2定点$${\mathrm{F}}$$、$${\mathrm{F}'}$$までの距離の和が一定である点$${\mathrm{P}}$$の軌跡を 楕円 といい,2定点$${\mathrm{F}}$$、$${\mathrm{F}'}$$をその 焦点 という。
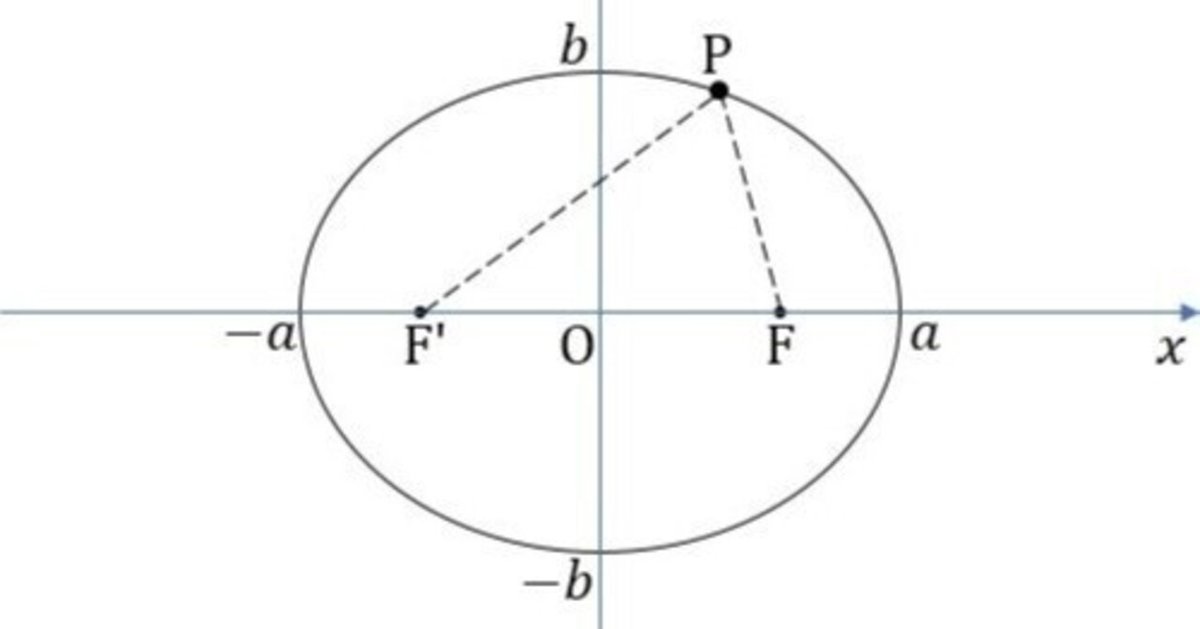
焦点が x 軸上にある楕円
$$
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \ \ (a > b > 0)
$$
[1] 中心は原点、長軸の長さ $${2a}$$、短軸の長さ $${2b}$$
[2] 焦点は2点$${(\sqrt{a^2-b^2},0), \ \ (-\sqrt{a^2-b^2},0)}$$
[3] 楕円は$${x}$$軸、$${y}$$軸、原点に関して対称である。
[4] 楕円上の点から2つの焦点までの距離の和は $${2a}$$
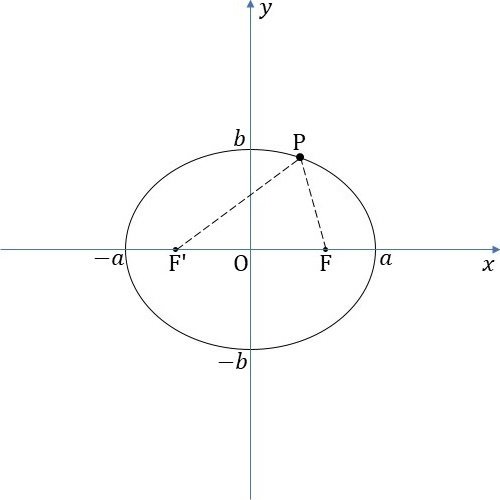
焦点が y 軸上にある楕円
$$
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \ \ (b > a > 0)
$$
[1] 中心は原点、長軸の長さ $${2b}$$、短軸の長さ $${2a}$$
[2] 焦点は2点$${(0,\sqrt{b^2-a^2}), \ \ (0,-\sqrt{b^2-a^2})}$$
[3] 楕円は$${x}$$軸、$${y}$$軸、原点に関して対称である。
[4] 楕円上の点から2つの焦点までの距離の和は $${2b}$$
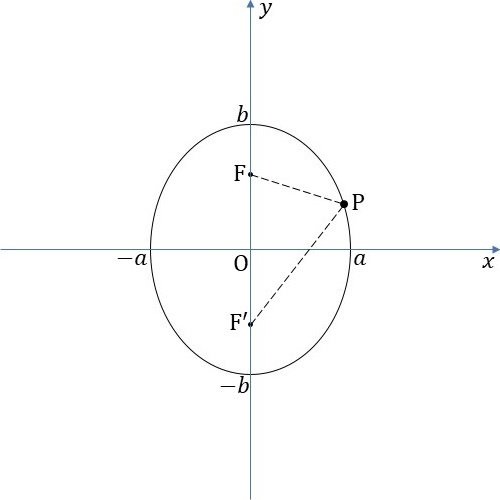
円と楕円
楕円
$$
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1
$$
は、円$${x^2+y^2=a^2}$$を$${x}$$軸をもとにして$${y}$$軸方向に$${b/a}$$倍に縮小または拡大して得られる曲線。
楕円を描く
では、楕円を描くプログラムを作成していきます。
問題1
中心が原点、2つの焦点が$${x}$$軸上にあり、次の条件を満たす楕円の方程式を求め、座標上に描け。
(1) 長軸の長さが$${6}$$、短軸の長さが$${4}$$
(2) 2つの焦点間の距離が$${6}$$、長軸の長さが$${10}$$
(3) 2点$${( \frac{\sqrt{3}}{2}, \frac{\sqrt{33}}{3} ), \ \ ( \frac{\sqrt{30}}{2}, \frac{\sqrt{6}}{3} ) }$$を通る
(4) 2点$${(\sqrt{7},0), \ \ (-\sqrt{7},0)}$$を焦点とし、短軸の長さが$${6}$$
アルゴリズム設計
楕円の方程式を求める
まず、問題1の楕円の方程式を求めてみます。基本的には、「中心が原点、2つの焦点が$${x}$$軸上」ですので、方程式は
$$
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \ \ (a > b > 0)
$$
の形になります。
(1)は、その条件から、
$$
2a = 6, \ \ 2b=4
$$
となるので、$${a=3,b=2}$$となり、方程式は、
$$
\frac{x^2}{3^2} + \frac{y^2}{2^2} = 1
$$
となります。
(2)は、条件から、
$$
2 \sqrt{a^2-b^2} = 6, \ \ 2a = 10
$$
となるので、$${a=5, b=4}$$となり、方程式は、
$$
\frac{x^2}{5^2} + \frac{y^2}{4^2} = 1
$$
となります。
(3)は、条件から、
$$
\frac{3}{4a^2}+\frac{33}{9b^2}=1, \ \ \frac{30}{4a^2}+\frac{6}{9b^2}=1
$$
となるので、$${a=3,b=2}$$となり、方程式は、
$$
\frac{x^2}{3^2} + \frac{y^2}{2^2} = 1
$$
となります。
(4)は、条件から、
$$
\sqrt{a^2-b^2} = \sqrt{7}, \ \ 2b = 6
$$
となるので、$${a=4,b=3}$$となり、方程式は
$$
\frac{x^2}{4^2} + \frac{y^2}{3^2} = 1
$$
となります。
(1)と(3)は同じ結果になっています。
楕円を描く関数 ellipse
問題1の楕円の方程式を求めることができたので、あとはこれらの楕円を描くだけです。Processingでは、楕円を描くための関数 ellipse が用意されています。
ellipse(a,b,c,d);a:楕円の中心の$${x}$$座標 float型
b:楕円の中心の$${y}$$座標 float型
c:楕円の幅 float型
d:楕円の高さ float型
この ellipse 関数を利用して$${xy}$$平面上に楕円を描いていきます。
プログラム
では、原点を中心とし、2つの焦点が$${x}$$軸上にある楕円を描くプログラムを作成していきます。
グラフを描くので、記事『高校数学をプログラミングで解く(数学I編)「1-0-2 グラフを描くための準備(その2)」』で準備した座標軸を描く関数 setAxes を利用します。以下の zip ファイルをダウンロードして展開または解凍してください。
そして、スケッチの名前(フォルダ名)を「draw_ellipse」と変更し、またスケッチ「draw_ellipse」内の「drawFunction.pde」ファイルの名前を「draw_ellipse.pde」に変更します。そして、pdeファイル「draw_ellipse.pde」をダブルクリックしてスケッチ「draw_ellipse」の開発環境ウィンドウを立ち上げます。そして、開発環境ウィンドウのタブ欄で「draw_ellipse」タブを選択して、そのテキストエリアのソースコードを以下のソースコード1に書き換えます。
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500);
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill();
stroke(0,0,0);
// (1) (3)
float a = 3.0;
float b = 2.0;
stroke(255,0,0);
draw_ellipse_w_focuses(a,b);
// (2)
a = 5.0;
b = 4.0;
stroke(0,255,0);
draw_ellipse_w_focuses(a,b);
// (4)
a = 4.0;
b = 3.0;
stroke(0,0,255);
draw_ellipse_w_focuses(a,b);
}
// 中心を原点、焦点をx軸またはy軸上とする楕円を描く関数
void draw_ellipse_w_focuses(
float a, // 楕円の幅の半分
float b // 楕円の高さの半分
){
// グラフを描画
float A, B; // キャンバス上での軸の長さ
A = width / 2.0 / x_range * a;
B = height / 2.0 / y_range * b;
ellipse(0.0,0.0,2.0*A,2.0*B);
// 焦点を描画
if(a > b){ // x軸方向に長軸がある場合
plot_point(sqrt(a*a-b*b),0.0);
plot_point(-sqrt(a*a-b*b),0.0);
} else if(a < b){ // y軸方向に長軸がある場合
plot_point(0.0,sqrt(b*b-a*a));
plot_point(0.0,-sqrt(b*b-a*a));
} else { // 円の場合
plot_point(0.0,0.0);
}
}
// 座標(x,y)に点をプロットする関数
void plot_point(
float x, // 点のx座標
float y // 点のy座標
){
float X, Y; // キャンバス上の座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
strokeWeight(5);
point(X, Y);
strokeWeight(1);
}ソースコード1 中心が原点、2つの焦点が$${x}$$軸上の楕円を描くプログラム
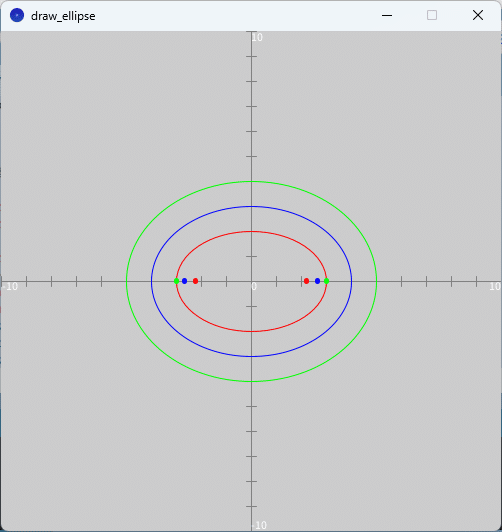
ソースコード1では、中心を原点、2つの焦点を$${x}$$軸または$${y}$$軸上とする楕円を描く関数 draw_ellipse_w_focuses を準備して利用しました。楕円を描くだけであれば、長軸や短軸の長さをキャンバス上のサイズに換算した上で、ellipse 関数を直接利用して描くこともできますが、今回は楕円と共に2つの焦点の位置もプロットするために draw_ellipse_w_focuses 関数を別途準備しました。なお、長軸が$${x}$$軸方向になるか、$${y}$$軸方向になるかで、焦点位置が変わってきますので、場合分けをしてプロットするようにしています。
「draw_ellipse」タブのテキストエリアをソースコード1に書き換えて、スケッチ「draw_ellipse」を実行すると、図3のように、実行ウィンドウのキャンバス上に問題1(1)と(3)の楕円が赤色、(2)の楕円が緑色、(4)の楕円が青色で描かれます。
一般的な楕円の軌跡を描く
上記の問題では、中心が原点、2つの焦点が$${x}$$軸上または$${y}$$軸上にある楕円を扱いましたが、今度は、より一般的な楕円の軌跡を考えてみます。つまり、異なる2定点(焦点)$${\mathrm{F}(a_1, b_1)}$$、$${\mathrm{F}'(a_2,b_2)}$$までの距離の和が$${r \ \ ( >\sqrt{(a_2-a_1)^2+(b_2-b_1)^2} )}$$となる点$${\mathrm{P}(x,y)}$$の軌跡を考えます。
問題2
2定点$${(4,1), (-3,-2)}$$までの距離の和が$${10}$$となる点$${\mathrm{P}(x,y)}$$の軌跡を描け。
アルゴリズム設計
この一般的な楕円の軌跡を描くにあたり、記事『高校数学をプログラミングで解く(数学II編)「2-5 軌跡と方程式」』で解説した方法を利用します。
つまり、$${xy}$$平面の描画範囲内の任意の点$${(x,y)}$$を取ってきて、その点と2定点との距離の和が$${r}$$になっているかどうかを確かめ、$${r}$$になっていればその点をキャンバス上の$${xy}$$平面にプロットし、$${r}$$になっていなければプロットしないというルールで行います。そして、プロットされた点が描く軌跡が楕円になっているかを確認します。なお、記事『高校数学をプログラミングで解く(数学III編)「1-4 複素数と図形(1)」』で作成したスケッチ「drawTrajectory_complex」でも同様の方法を利用しているので、そちらの解説も確認してみてください。
プログラム
先程作成したスケッチ「draw_ellipse」を再利用します。
スケッチ「draw_ellipse」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「draw_ellipse_general」と変更し、またスケッチ「draw_ellipse_general」内の「draw_ellipse.pde」ファイルの名前を「draw_ellipse_general.pde」に変更します。そして、pdeファイル「draw_ellipse_general.pde」をダブルクリックしてスケッチ「draw_ellipse_general」の開発環境ウィンドウを立ち上げます。
問題2の一般的な楕円の軌跡を描くプログラムを作成していきます。
// 楕円の定義を満たす点が描く図形
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500,P2D); // widthとheightは同じにしておく
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill(); // グラフの中身を塗りつぶさない
stroke(0,0,0); // グラフの線の色を黒色に設定
// 点の生成回数
int n = 1000000;
// マージン
float e = 0.001;
// 1つ目の焦点の座標
float a1 = 4.0;
float b1 = 1.0;
// 2つ目の焦点の座標
float a2 = -3.0;
float b2 = -2.0;
// 距離の和
float r = 10.0;
float x, y; // 任意の点の座標
float l1; // 1つ目の焦点との距離
float l2; // 2つ目の焦点との距離
for(int i=0; i<n; i++){
// 任意の複素数を生成
x = random(-x_range, x_range);
y = random(-y_range, y_range);
// 2つの焦点との距離の和がrになればプロット
stroke(255,0,0);
l1 = sqrt((x-a1)*(x-a1)+(y-b1)*(y-b1));
l2 = sqrt((x-a2)*(x-a2)+(y-b2)*(y-b2));
if( abs(l1+l2-r) < e ){
plot_point(x,y);
}
}
// 焦点をプロット
stroke(0,0,255);
plot_point(a1,b1);
plot_point(a2,b2);
}
// 座標(x,y)に点をプロットする関数
void plot_point(
float x, // 点のx座標
float y // 点のy座標
){
float X, Y; // キャンバス上の座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
strokeWeight(5);
point(X, Y);
strokeWeight(1);
}ソースコード2 一般的な楕円の軌跡を描くプログラム
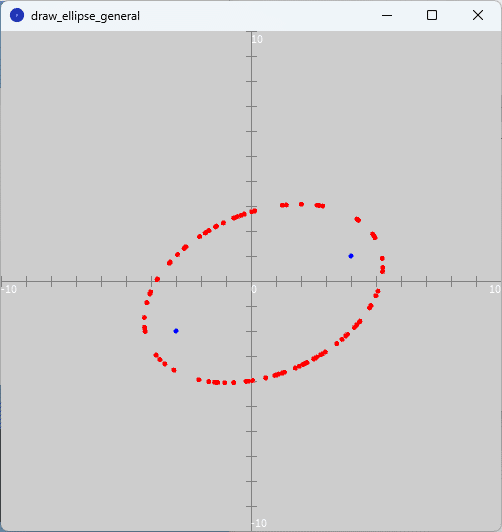
スケッチ「draw_ellipse_general」の「draw_ellipse_general」タブを選択してそのテキストエディタ部分をソースコード2で書き換えて実行すると、図4のように、実行ウィンドウのキャンバスの$${xy}$$平面上に、問題2の楕円の軌跡が赤色、楕円の2つの焦点が青色で描かれます。
まとめ
今回は、数学IIIで学ぶ「楕円」について、楕円を描くプログラムを2つ作成しました。
1つ目は、原点を中心とし、焦点が$${x}$$軸上または$${y}$$軸上にある楕円を描くプログラムを作成しました。Processingでは楕円を描く関数 ellipse があります。プログラムでは、ellipse 関数で描かれる楕円にその2つの焦点も描くように関数 draw_ellipse_w_focuses を準備して利用しました。
2つ目は、楕円の定義「異なる2定点(焦点)$${\mathrm{F}}$$、$${\mathrm{F}'}$$までの距離の和が$${r}$$となる点$${\mathrm{P}}$$の軌跡」に基づいて一般的な楕円の軌跡を描くプログラムを作成しました。こちらについては、$${xy}$$平面上の任意の点を取ってきて定義を満たせば、$${xy}$$平面上にプロットするという方法を取りました。
定義に基づいた一般的な楕円は、原点を中心とし、焦点が$${x}$$軸上または$${y}$$軸上にある楕円を平行移動や回転したものになっています。これについては別の記事で紹介します。
参考文献
改訂版 教科書傍用 スタンダード・オリジナル 数学III(数研出版、ISBN9784410209567)
演習問題
円$${x^2+y^2=25}$$を次のように拡大または縮小した曲線の方程式を求め、その結果を図示するプログラムを作成してください。
(1) $${x}$$軸をもとにして$${y}$$軸方向に$${4/5}$$倍
(2) $${y}$$軸をもとにして$${x}$$軸方向に$${2}$$倍
演習問題の解答例
ここから先は
Amazonギフトカード5,000円分が当たる
この記事が気に入ったらチップで応援してみませんか?
