高校数学をプログラミングで解く（数学B編）「1-1 ベクトルの演算」

2024年4月27日 06:35

マガジンリスト　＞　数学B編 1.平面上のベクトル　＞　1-1 ベクトルの演算

はじめに

今回は、数学Bで学ぶ「ベクトルの演算」について、ベクトルの和や差、実数倍などの基本的な演算をプログラミング言語 Processing でどのように扱うのかを解説し、実際にそれらの演算を行い、それらのベクトルを表示するプログラムを作成します。

ベクトルの演算

まず、ベクトルの基本的な演算についてまとめておきます。なお、以下で$${k, l}$$は実数とし、$${\vec{a} = (a_1, a_2), \ \vec{b} = (b_1, b_2)}$$とします。

ベクトルの相等

$$
\begin{array}{rcl}
\vec{a} = \vec{b} & \Leftrightarrow & \vec{a} \mathrm{と} \vec{b} \mathrm{の向きが同じで大きさが等しい} \\
& \Leftrightarrow & (a_1, a_2) = (b_1, b_2) \\
& \Leftrightarrow & a_1 = b_1, a_2 = b_2
\end{array}
$$

ベクトルの和

$$
\vec{a} + \vec{b} = (a_1, a_2) + (b_1, b_2) = (a_1+b_1, a_2+b_2)
$$

ベクトルの差

$$
\vec{a} - \vec{b} = (a_1, a_2) - (b_1, b_2) = (a_1-b_1, a_2-b_2)
$$

ベクトルの大きさ

$$
|\vec{a}| = \sqrt{a_1^2+a_2^2}
$$

ベクトルの実数倍

$$
k \vec{a} = ( ka_1, ka_2)
$$

演算法則

$$
\vec{a} + \vec{b} = \vec{b} + \vec{a} = (a_1+b_1, a_2+b_2) = (b_1+a_1, b_2+a_2) \\
(\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c}) \\
k(l \vec{a}) = (kl) \vec{a} = k(la_1, la_2) = (kla_1, kla_2) \\
(k+l) \vec{a} = k \vec{a} + l \vec{a} = (ka_1, ka_2) + (la_1, la_2) = ((k+l)a_1, (k+l)a_2) \\
k(\vec{a}+\vec{b}) = k\vec{a} + k \vec{b} = (k(a_1+b_1), k(a_2+b_2))
$$

ベクトルの平行条件

$${ \vec{a} \neq \vec{0}, \vec{b} \neq \vec{0} }$$のとき、

$$
\vec{a} /\!\!/ \vec{b} \Leftrightarrow \vec{b}=k \vec{a} \mathrm{となる実数}k\mathrm{がある}
$$

ベクトルの分解

$${ \vec{a} \neq \vec{0}, \vec{b} \neq \vec{0} }$$で、$${\vec{a}}$$と$${\vec{b}}$$が平行でないとき、任意のベクトル$${\vec{p}}$$は、適当な実数$${s, t}$$を用いて、$${\vec{p}=s \vec{a} + t \vec{b} }$$の形でただ１通りに表すことができる。

座標とベクトル

$${A(a_1, a_2), B(b_1, b_2)}$$とする。

$$
\overrightarrow{AB} = (b_1-a_1, b_2-a_2), \ \ | \overrightarrow{AB}| = \sqrt{ (b_1-a_1)^2+(b_2-a_2)^2}
$$

Processingでベクトルを扱う

ベクトルの演算についてまとめたので、次にプログラミング言語でのベクトルの扱い方をまとめていきます。プログラミング言語によりベクトルを扱っていないものもありますが、プログラミング言語 Processing ではベクトルを扱うための PVector クラスというものが用意されています。ここでは、PVector クラスを用いてベクトル演算を行う方法をまとめていきます。

ベクトルの生成

まず、プログラムで利用するベクトルの生成について解説します。以下のソースコードのように書くことで変数 a をベクトル$${\vec{a}}$$のように扱うことができます。

PVector a = new PVector(a1,a2);

各引数は次のようになっています。

a1：ベクトルの$${x}$$成分　float型
a2：ベクトルの$${y}$$成分　float型

ベクトルの和

次に、ベクトルの和について解説します。２つのベクトルの和は単純に”＋”の記号を利用して和を取れるわけではないことに注意してください。２つのベクトルの和を取るためには add 関数を利用します。

PVector a = new PVector(a1,a2);
PVector b = new PVector(b1,b2);
b.add(a);

これでベクトルの和は計算できるわけですが、１点注意が必要です。それは、「b.add(a);」と書いた場合、「変数 b のベクトルに変数 a のベクトルを加えて、変数 b に代入する」ということになります。つまり、変数 b のベクトルの値は変更されるわけです。
そこで、$${\vec{b}}$$の値は変更せずに、$${\vec{c} = \vec{b}+\vec{a}}$$を計算したい場合は以下のように書きます。

PVector a = new PVector(a1,a2);
PVector b = new PVector(b1,b2);
PVector c = b.copy().add(a); // b+aをcに代入、bは変更なし

つまり、変数 b に入っているベクトルをコピーして、そのコピーに変数 a に入っているベクトルを加え、そのベクトルを変数 c に代入するようにします。

ベクトルの差

ベクトルの差について解説します。ベクトルの和と同様に、２つのベクトルの差は単純に”－”の記号を利用して差を取れるわけではないです。２つのベクトルの差を取るためには sub 関数を利用します。

PVector a = new PVector(a1,a2);
PVector b = new PVector(b1,b2);
PVector c = b.copy().sub(a); // b-aをcに代入、bは変更なし
b.sub(a); // bをb-aに変更

ベクトルの大きさ

ベクトルの大きさについて解説します。ベクトルの大きさは定義通りにベクトルの成分を用いて計算することもできますが、PVectorクラスでは mag 関数を利用して大きさを求めることができます。

PVector a = new PVector(a1,a2);
float r = a.mag(); // ベクトルaの大きさ

なお、mag 関数は引数を取らず、ベクトルの大きさをfloat型の値で返します。

ベクトルの実数倍

ベクトルの実数倍について解説します。ベクトルの実数倍は mult 関数を利用します。

float k = 2.0;
PVector a = new PVector(a1,a2);
PVector b = a.copy().mult(k); // ベクトルaをk倍してbに代入
a.mult(k); // ベクトルaをk倍する

各引数は次のようになっています。

k：ベクトルを k 倍にする　float型

ベクトル演算のプログラム

では、上記で説明した PVector クラスを用いてベクトル演算を行う方法で、実際にプログラムを作成してみます。具体的には、

$$
\vec{a} = (5,1), \vec{b}=(1,4), \ k=-1.5
$$

として、

$$
\vec{c} = \vec{b} + \vec{a}, \ \vec{d} = \vec{b} - \vec{a}, \ \vec{e} = k \vec{a}
$$

をそれぞれ計算して、それらのベクトルを実行ウィンドウのキャンバスに描いていきます。なお、ベクトルは、記事『高校数学をプログラミングで解く（数学B編）「1-0 ベクトルを描く」』で解説した arrow 関数を用いて描いていきます。

// ベクトルの演算を行い、ベクトルを描画する
void setup(){
  size(500,500,P2D); // widthとheightは同じにしておく
  noLoop();
  float range = 10.0; // x軸及びy軸の表示範囲 -rangeからrangeまで
  setAxes(range, range); // 座標軸の準備
  
  // 以下にグラフを描いていく
  noFill(); // グラフの中身を塗りつぶさない
  stroke(0,0,0); // グラフの線の色を黒色に設定

  // ベクトルの準備
  float k = -1.5;
  PVector a = new PVector(5.0, 1.0);
  PVector b = new PVector(1.0, 4.0);
  
  // ベクトルの演算
  PVector c = b.copy().add(a);
  PVector d = b.copy().sub(a);
  PVector e = a.copy().mult(k);
  
  // コンソールにベクトルの成分を出力
  println("a:", a);
  println("b:", b);  
  println("c=b+a:", c);  
  println("d=b-a:", d);  
  println("e=ka:", e);  
  
  // キャンバスにベクトルを描画
  arrow(0.0,0.0,a.x,a.y,range);
  arrow(0.0,0.0,b.x,b.y,range);
  stroke(255,0,0); // ベクトルcは赤色
  arrow(0.0,0.0,c.x,c.y,range);
  stroke(0,0,255); // ベクトルdは青色
  arrow(0.0,0.0,d.x,d.y,range);
  stroke(0,255,0); // ベクトルeは緑色
  arrow(0.0,0.0,e.x,e.y,range);

}

ソースコード1　ベクトルの演算を行い、それらを描画するプログラム

スケッチ「calcanddrawVector」を準備し、その「calcanddrawVector」フォルダに、記事『高校数学をプログラミングで解く（数学B編）「1-0 ベクトルを描く」』で作成したスケッチ「drawVector」のフォルダの中にある「setAxes.pde」ファイルと「setArrow.pde」ファイルをコピーして、ソースコード1を「calcanddrawVector」タブのテキストエディタ部分に書いて実行すると、図1のように、コンソールに各ベクトルの成分が

a: [ 5.0, 1.0, 0.0 ]
b: [ 1.0, 4.0, 0.0 ]
c=b+a: [ 6.0, 5.0, 0.0 ]
d=b-a: [ -4.0, 3.0, 0.0 ]
e=ka: [ -7.5, -1.5, -0.0 ]

と表示され、また、図2のように、実行ウィンドウのキャンバスにそれぞれのベクトルが矢印で描かれます。

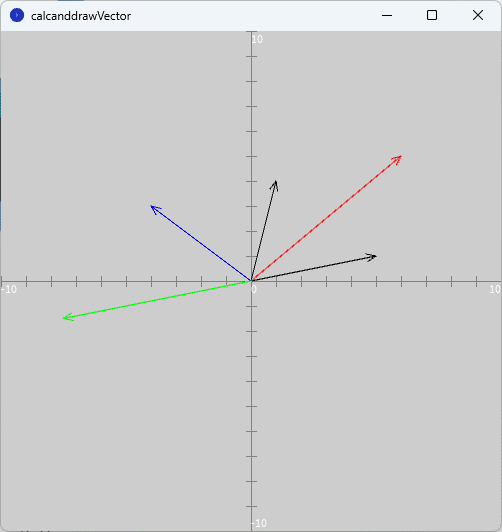
なお、図1のコンソールに出力されたベクトルの成分は３つの成分からなっています。これは本来 PVector クラスが空間ベクトルとして利用することを前提にしているからです。ただ、PVector クラスは平面ベクトルにも利用でき、そのとき$${z}$$成分は0.0となっています。

まとめ

今回は、数学Bで学ぶ「ベクトルの演算」について、ベクトルの和や差、実数倍などの基本的な演算をプログラミング言語 Processing でどのように扱うのかを解説し、実際にそれらの演算を行い、それらのベクトルを表示するプログラムを作成しました。
今回は基礎的なベクトル演算を扱いましたが、ベクトルを利用するための PVector クラスは今後何度も出てきますし、いろいろなところで応用されていきます。何度も利用していくうちに少しずつベクトルの扱いに慣れていってください。

参考文献

改訂版教科書傍用スタンダード数学B（数研出版、ISBN9784410209468）

この記事が気に入ったらサポートをしてみませんか？