見出し画像

高校数学をプログラミングで解く（数学B編）「1-0 ベクトルを描く」

MK's papa

マガジンリスト　＞　数学B編 1.平面上のベクトル　＞　1-0 ベクトルを描く


はじめに

今回はキャンバス上に設定された座標軸を基準としてベクトルを描くための関数を作成し、その利用方法について説明していきます。
なお、ベクトルを描くための関数を作成するにあたり、そらたまごさんの『Processingで矢印を書く方法（2次元）』の記事を参考にさせてもらいました。

Processingでベクトルを描く

数学Bから、いよいよベクトルの演算が入ってきます。
Processingでは、ベクトルを扱うためのPVectorクラスというものが用意されており、PVectorクラスを用いてほとんどのベクトル演算を行うことができます。PVectorクラスの扱いについては記事『高校数学をプログラミングで解く（数学B編）「1-1 ベクトルの演算」』で紹介します。
一方で、Processingではベクトルを描くための関数などは用意されていません。ベクトルは図示しながら学んだ方がよいと考えていますので、これは少し不便です。そこで、この記事では、ベクトルを描くための関数を自作します。そして、今後のベクトルの問題を考える際に利用していきます。

ベクトル描画のイメージ

今回描くベクトルのイメージを図1に示します。

図1　ベクトル描画のイメージ

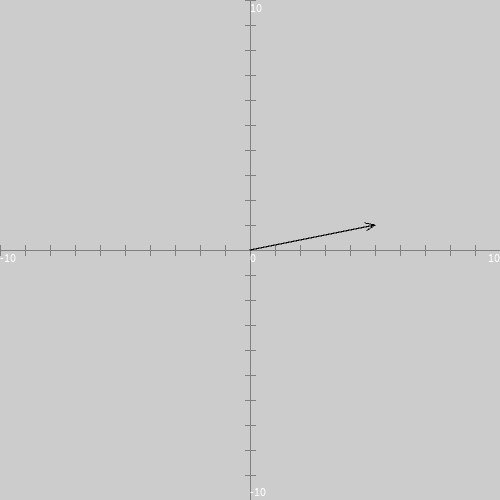
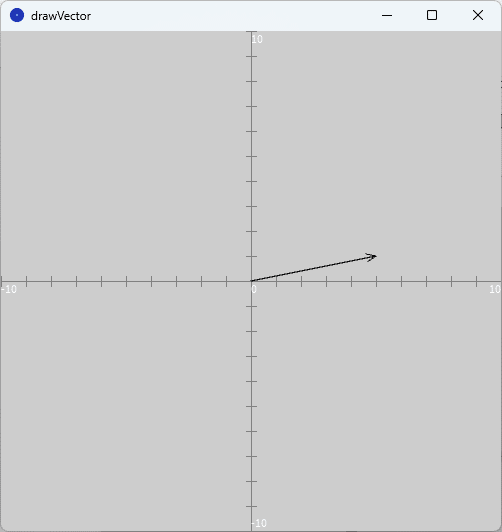
図1は、$${x}$$軸方向と$${y}$$軸方向がともに$${-10}$$から$${10}$$までの範囲の領域に、ベクトル$${(5,1)}$$を描画した例になります。

ベクトルを描くための関数の準備

図1のようなベクトルを描くための関数arrowを作成します。

// ベクトルを表示する関数
// ※widthとheight、及びsetAxes関数のx_rangeとy_rangeは同じ値にしておく
void arrow(
  float start_x, // ベクトルの始点のx座標
  float start_y, // ベクトルの始点のy座標
  float end_x, // ベクトルの終点のx座標
  float end_y, // ベクトルの終点のx座標
  float range // グラフの表示範囲を-rangeからrangeまでとする
){
  start_x *= width / 2.0 / range;
  start_y *= width / 2.0 / range;
  end_x *= width / 2.0 / range;
  end_y *= width / 2.0 / range;
  float arrowLength = 10.0;
  float arrowAngle = 0.4;
  float angle =  atan2(end_y-start_y, end_x-start_x);
  line(start_x, start_y, end_x, end_y);
  pushMatrix();
  translate(end_x, end_y);
  rotate(angle);
  line(0, 0, -arrowLength*cos(arrowAngle), arrowLength*sin(arrowAngle));
  line(0, 0, -arrowLength*cos(arrowAngle), -arrowLength*sin(arrowAngle));
  popMatrix();
}

ソースコード1　ベクトルを描くための関数

ソースコード1のarrow関数の引数は以下の通りとなります。

図2　ベクトルを描くための関数の引数

start_x：ベクトルの始点の$${x}$$座標　float型
start_y：ベクトルの始点の$${y}$$座標　float型
end_x：ベクトルの終点の$${x}$$座標　float型
end_y：ベクトルの終点の$${y}$$座標　float型
range：表示範囲（$${x}$$軸方向、$${y}$$軸方向共に-rangeからrangeまで）　float型

ベクトルを描くための関数をpdeファイルに保存

今回作成したベクトルを描くための関数 arrow （ソースコード1）は以前の記事『高校数学をプログラミングで解く（数学I編）「1-0-2 グラフを描くための準備（その2）」』で作成した setAxes 関数と一緒に利用します。そのため、この setAxes 関数を記述したpdeファイル「setAxes.pde」を再利用します。ただ、この setAxes 関数を呼び出すときに setup 関数内に記述するコードを一から作成することは少し手間なので、記事『高校数学をプログラミングで解く（準備編）「3-3 pdeファイルの再利用」』で説明したpdeファイルの再利用方法のうち『スケッチごとコピーする方法』で行います。

① 記事『高校数学をプログラミングで解く（数学I編）「1-0-2 グラフを描くための準備（その2）」』で作成したスケッチ「drawAxes」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「drawVector」と変更し、またスケッチ「drawVector」内の「drawAxes.pde」ファイルの名前を「drawVector.pde」に変更します（図3）。

図3　スケッチ「drawVector」のフォルダ

② pdeファイル「drawVector.pde」をダブルクリックしてスケッチ「drawVector」の開発環境ウィンドウを立ち上げます（図4）。その結果、開発環境ウィンドウのタブ欄には「drawVector」と「setAxes」の２つのタブが並んだ状態で表示されます。

図4　スケッチ「drawVector」の開発環境ウィンドウ

③ スケッチ「drawVector」の開発環境ウィンドウのタブ欄にある▼のボタンを押して「新規タブ」を選択し、新たに「setArrow」タブを追加します（図5）。

図5　「setArrow」タブを追加

また、このとき、スケッチ「drawVector」のフォルダに、pdeファイル「setArrow.pde」が追加されます（図6）。

図6　「setArrow.pde」ファイルの追加

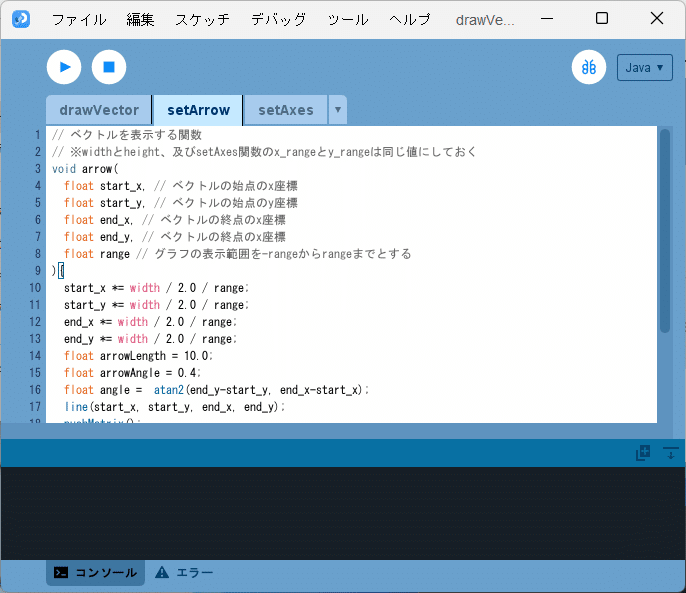
④ 「setArrow」タブを選択した状態で、そのテキストエリアに arrow 関数（ソースコード1）を記述します（図7）。

図7　arrow関数を記述

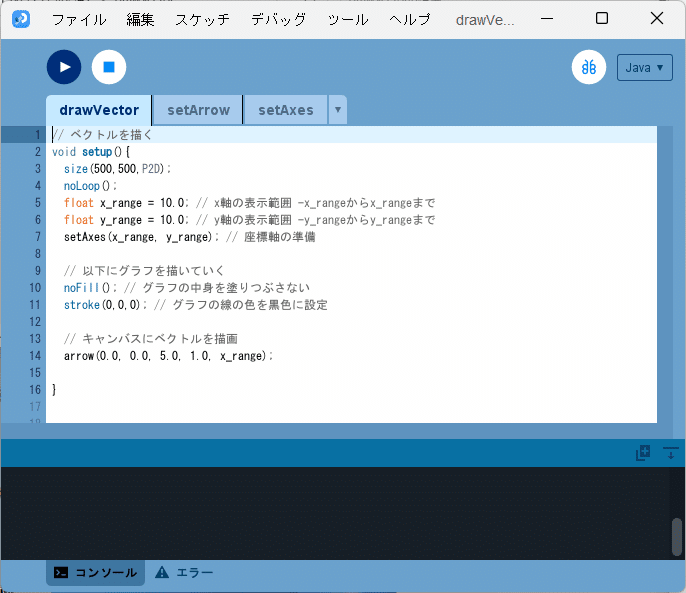
⑤ 「drawVector」タブを選択し、そのテキストエリアに arrow 関数を呼び出すコードを追記していきます（ソースコード2、図8）。

// ベクトルを描く
void setup(){
  size(500,500,P2D);
  noLoop();
  float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
  float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで 
  setAxes(x_range, y_range); // 座標軸の準備
  
  // 以下にグラフを描いていく
  noFill(); // グラフの中身を塗りつぶさない
  stroke(0,0,0); // グラフの線の色を黒色に設定

  // キャンバスにベクトルを描画
  arrow(0.0, 0.0, 5.0, 1.0, x_range);

}

ソースコード2　arrow 関数を呼び出してベクトルを描くプログラム

図8　arrow 関数を呼び出すコードを記述

⑥ 最後に、実行ボタンを押すと、実行ウィンドウのキャンバスに図1と同じベクトルを描いた画像が表示されます（図9）。

図9　ベクトルの描画

setArrow.pdeファイルの再利用

ベクトルを描くための関数 arrow をpdeファイル「setArrow.pde」に保存したので、今後ベクトルを描く際にはpdeファイル「setArrow.pde」を再利用していきます。ただ、基本的に arrow 関数は setAxes 関数と一緒に利用されますので、再利用方法としては、記事『高校数学をプログラミングで解く（準備編）「3-3 pdeファイルの再利用」』で説明した『スケッチごとコピーする方法』で行った方がよいでしょう。
今度は、ベクトル$${(1,5)}$$を描画するプログラムの作成を例にして再利用方法について説明します。

① スケッチ「drawVector」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「drawVector2」と変更し、またスケッチ「drawVector2」内の「drawVector.pde」ファイルの名前を「drawVector.pde」に変更します（図10）。

図10　スケッチ「drawVector2」のフォルダ

② pdeファイル「drawVector2.pde」をダブルクリックしてスケッチ「drawVector2」の開発環境ウィンドウを立ち上げます（図11）。

図11　スケッチ「drawVector2」の開発環境ウィンドウ

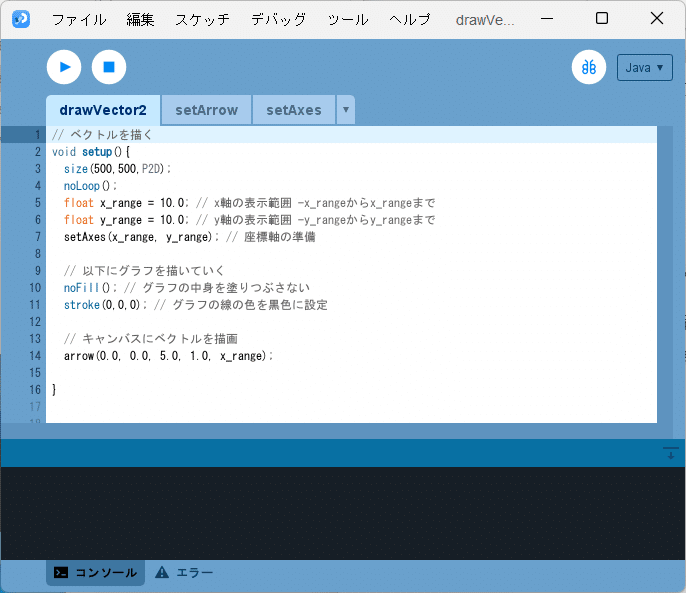
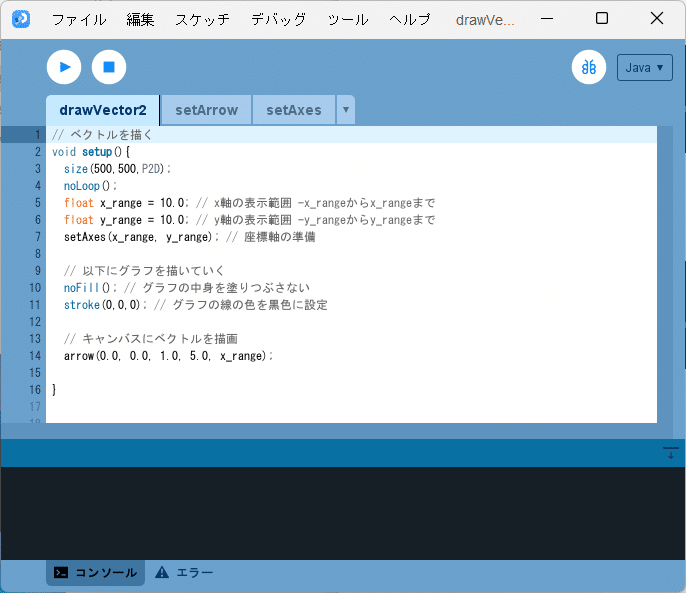
③ 「drawVector2」タブに記述されたソースコードで、

  // キャンバスにベクトルを描画
  arrow(0.0, 0.0, 5.0, 1.0, x_range);

の部分を

  // キャンバスにベクトルを描画
  arrow(0.0, 0.0, 1.0, 5.0, x_range);

に書き換えます（図12）。

図12　arrow関数の引数を書き換える

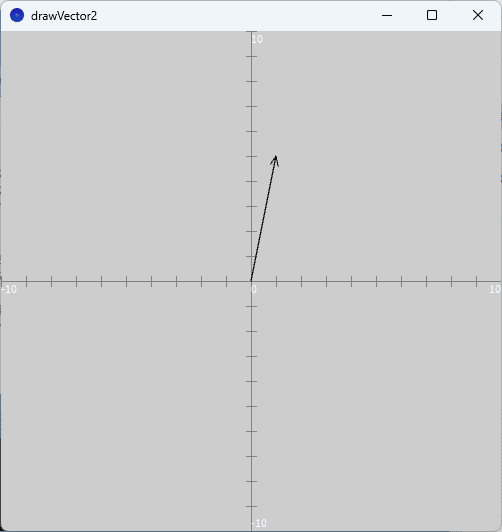
④ 最後に、実行ボタンを押すと、実行ウィンドウのキャンバスにベクトル$${(1,5)}$$を描いた画像が表示されます（図13）。

図13　キャンバスにベクトル(1.5)が描かれる

以上のように、今後ベクトルを描くプログラムを書く場合、スケッチ「drawVector」を再利用すると、比較的手間がなくベクトルを描くことができます。

ベクトルを描く関数の解説

『高校数学をプログラミングで解く』の趣旨とは少しずれますが、ベクトルを描く関数について少し解説しておきます。

プログラムの解説1「座標軸とベクトルのスケールを合わせる」

まず、ベクトルを描く関数（ソースコード1）の

  start_x *= width / 2.0 / range;
  start_y *= width / 2.0 / range;
  end_x *= width / 2.0 / range;
  end_y *= width / 2.0 / range;

の部分です。この部分は、座標軸とベクトルのスケールを合わせる処理を行っています。
今回、$${x}$$軸方向と$${y}$$軸方向がともに$${-10}$$から$${10}$$までの範囲の領域がキャンバスの幅や高さと一致するように設定しました。これを考慮すると、たとえば、点$${(-10,0)}$$はキャンバス上の$${(-\mathrm{width}/2,0)}$$にプロットされ、点$${(10,0)}$$はキャンバス上の$${(\mathrm{width}/2,0)}$$にプロットされることになるはずです。つまり、点（start_x, start_y）から点（end_x, end_y）へのベクトルをキャンバス上に描く場合は、そのままのスケールでキャンバス上に描くのではなく、キャンバス上の座標に変換してから描く必要があります。その変換を行っています。記事『高校数学をプログラミングで解く（数学I編）「1-0-1 グラフを描くための準備（その1）」』でも同様の解説を行っていますので、そちらも参考にしてください。

プログラムの解説2「ベクトルを描くためのパラメータ」

次に、ベクトルを描く関数（ソースコード1）の

  float arrowLength = 10.0;
  float arrowAngle = 0.4;
  float angle =  atan2(end_y-start_y, end_x-start_x);

の部分です。この部分は、ベクトルを描くための各種パラメータを設定しています（図14）。
arrowLength：矢印の傘の部分の長さ　float型
arrowAngle：矢印の傘のベクトル方向との角度（ラジアン）　float型
angle：矢印と$${x}$$軸正の向きとの角度（ラジアン）　float型

図14　ベクトルを描くためのパラメータ

特に、angleの値を求めるために、atan2関数を利用しています。

float atan2(y, x);

このatan2関数は、ベクトル$${(x,y)}$$と$${x}$$軸との間の角度（ラジアン）を求める関数で、引数は以下の通りです。
y：ベクトルの$${y}$$方向の成分　float型
x：ベクトルの$${x}$$方向の成分　float型

引数の順番が「x, y」の順ではなく、「y, x」の順番になっていることに注意してください。

プログラムの解説3「ベクトルの矢印の傘の部分を描く」

最後に、ベクトルを描く関数（ソースコード1）の

  pushMatrix();
  translate(end_x, end_y);
  rotate(angle);
  line(0, 0, -arrowLength*cos(arrowAngle), arrowLength*sin(arrowAngle));
  line(0, 0, -arrowLength*cos(arrowAngle), -arrowLength*sin(arrowAngle));
  popMatrix();

の部分です。この部分は、ベクトルの矢印の傘の部分を描くためのコードです。
ポイントは、この部分の最初と最後を pushMatrix 関数と popMatrix 関数とで挟んでいるところです。書籍『Processingをはじめよう 第２版（オライリー・ジャパン、オーム社、ISBN9784873117737）』によると、
pushMatrix()　現在の座標系をスタックに保存する
popMatrix()　元の座標系をスタックから取り出す
となっています。初学者にはわかりにくいかもしれませんので、pushMatrix 関数と popMatrix 関数とを利用したときのイメージをお伝えすると、
キャンバス上に透明のシートを一枚かぶせて pushMatrix 関数と popMatrix 関数の間に記述したコードはすべてこのシート上に対して行われる処理である
と考えることができます。以下でもう少し詳細に説明します。

① 説明のために、スケッチ「drawVector」の arrow 関数（ソースコード1）内で、pushMatrix 関数から popMatrix 関数までのコードを除いてみます（ソースコード3）。

void arrow(
  float start_x, // ベクトルの始点のx座標
  float start_y, // ベクトルの始点のy座標
  float end_x, // ベクトルの終点のx座標
  float end_y, // ベクトルの終点のx座標
  float range // グラフの表示範囲を-rangeからrangeまでとする
){
  start_x *= width / 2.0 / range;
  start_y *= width / 2.0 / range;
  end_x *= width / 2.0 / range;
  end_y *= width / 2.0 / range;
  float arrowLength = 10.0;
  float arrowAngle = 0.4;
  float angle =  atan2(end_y-start_y, end_x-start_x);
  line(start_x, start_y, end_x, end_y);
}

ソースコード3　arrow関数の pushMatrix 関数から popMatrix 関数までのコードを除外

そして、スケッチ「drawVector」を実行してみると、図15のように、キャンバス上にはベクトルの方向の線分だけが表示されます。

図15　ベクトルの方向を表す線分

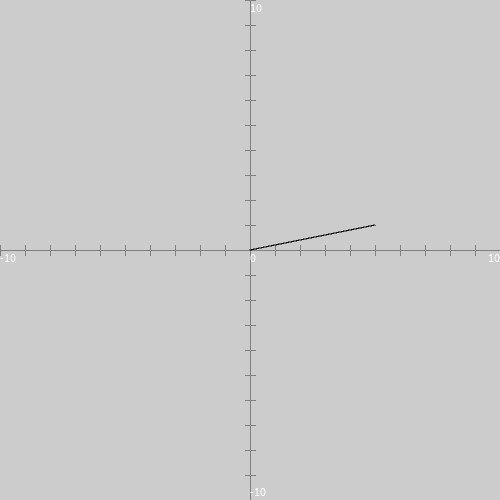
② 次に、ソースコード3に pushMatrix 関数と popMatrix 関数のみを追記してみます（ソースコード4）。

void arrow(
  float start_x, // ベクトルの始点のx座標
  float start_y, // ベクトルの始点のy座標
  float end_x, // ベクトルの終点のx座標
  float end_y, // ベクトルの終点のx座標
  float range // グラフの表示範囲を-rangeからrangeまでとする
){
  start_x *= width / 2.0 / range;
  start_y *= width / 2.0 / range;
  end_x *= width / 2.0 / range;
  end_y *= width / 2.0 / range;
  float arrowLength = 10.0;
  float arrowAngle = 0.4;
  float angle =  atan2(end_y-start_y, end_x-start_x);
  line(start_x, start_y, end_x, end_y);
  pushMatrix();
  popMatrix();
}

ソースコード4　arrow関数にpushMatrix関数とpopMatrix関数を追記

スケッチ「drawVector」を実行してみると、結果は図15と変わりませんが、先に述べたように、イメージとしてはキャンバス上に透明のシートを一枚かぶせたような状態になっています（図16）。なお、ポイントとしては、この透明のシートにはキャンバスと同じ座標系が設定されているということです。

図16　透明のシートを重ねたイメージ

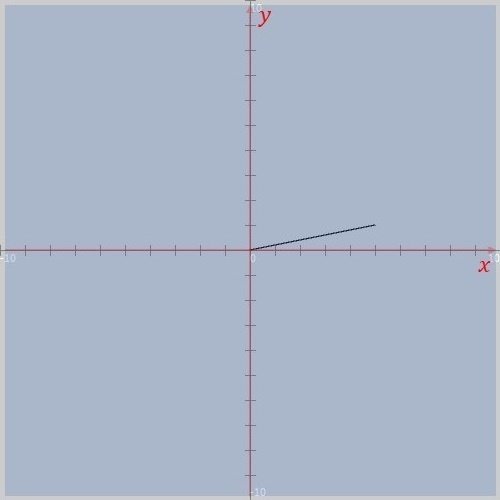
③ 次は、ソースコード4の pushMatrix 関数と popMatrix 関数との間に translate 関数を追記してみます（ソースコード5）。

void arrow(
  float start_x, // ベクトルの始点のx座標
  float start_y, // ベクトルの始点のy座標
  float end_x, // ベクトルの終点のx座標
  float end_y, // ベクトルの終点のx座標
  float range // グラフの表示範囲を-rangeからrangeまでとする
){
  start_x *= width / 2.0 / range;
  start_y *= width / 2.0 / range;
  end_x *= width / 2.0 / range;
  end_y *= width / 2.0 / range;
  float arrowLength = 10.0;
  float arrowAngle = 0.4;
  float angle =  atan2(end_y-start_y, end_x-start_x);
  line(start_x, start_y, end_x, end_y);
  pushMatrix();
  translate(end_x, end_y);
  popMatrix();
}

ソースコード5　pushMatrix 関数と popMatrix 関数との間に translate 関数を追記

translate 関数は座標系の位置をずらしますが、今回は pushMatrix 関数と popMatrix 関数との間に追記していますので、キャンバス自体の座標系ではなく、透明なシートの座標系の位置が移動します。今回 translate 関数による移動先の位置がベクトルの終点の座標位置（end_x, end_y）となっているので、イメージとしては、図17のようになります。なお、この段階でもスケッチ「drawVector」の実行結果としては図15と変わりません。

図17　透明のシートの座標系の移動（イメージ）

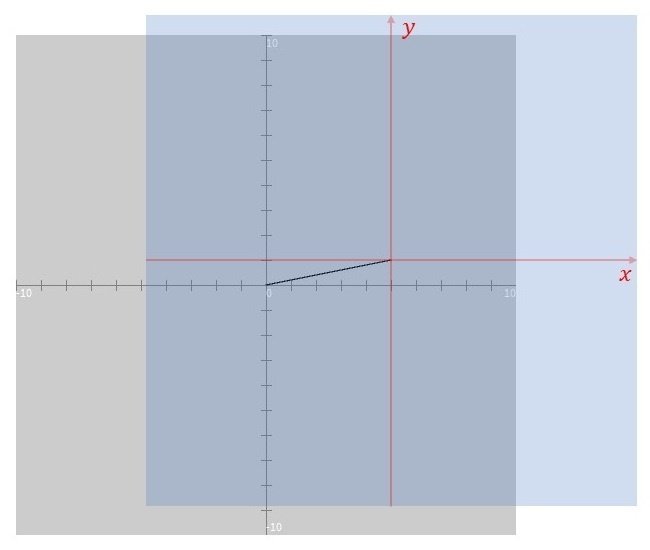
④ 今度は、ソースコード5の pushMatrix 関数と popMatrix 関数との間に rotate 関数を追記してみます（ソースコード6）。

void arrow(
  float start_x, // ベクトルの始点のx座標
  float start_y, // ベクトルの始点のy座標
  float end_x, // ベクトルの終点のx座標
  float end_y, // ベクトルの終点のx座標
  float range // グラフの表示範囲を-rangeからrangeまでとする
){
  start_x *= width / 2.0 / range;
  start_y *= width / 2.0 / range;
  end_x *= width / 2.0 / range;
  end_y *= width / 2.0 / range;
  float arrowLength = 10.0;
  float arrowAngle = 0.4;
  float angle =  atan2(end_y-start_y, end_x-start_x);
  line(start_x, start_y, end_x, end_y);
  pushMatrix();
  translate(end_x, end_y);
  rotate(angle);
  popMatrix();
}

ソースコード6　pushMatrix 関数と popMatrix 関数との間に rotate 関数を追記

rotate 関数は座標系を回転しますが、③の translate 関数と同様、pushMatrix 関数と popMatrix 関数との間に追記していますので、キャンバス自体の座標系ではなく、透明なシートの座標系を回転します。今回 rotate 関数による回転の角度は angle（ベクトルの向きと$${x}$$軸正の向きとの角度）となっているので、イメージとしては、図18のようになります。なお、この段階でもスケッチ「drawVector」の実行結果としては図15と変わりません。

図18　透明のシートの座標系の回転（イメージ）

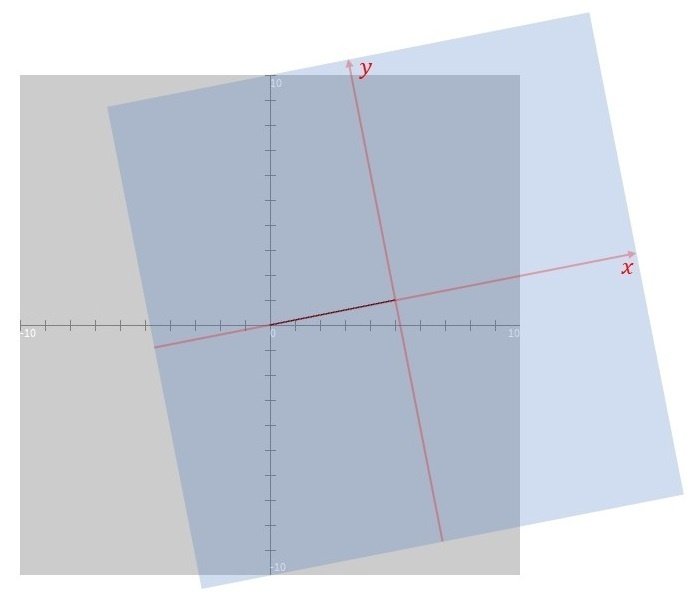
⑤ 最後に、ソースコード6の pushMatrix 関数と popMatrix 関数との間に２つの line 関数を追記します（ソースコード7）。これは元の arrow 関数と一致します。

void arrow(
  float start_x, // ベクトルの始点のx座標
  float start_y, // ベクトルの始点のy座標
  float end_x, // ベクトルの終点のx座標
  float end_y, // ベクトルの終点のx座標
  float range // グラフの表示範囲を-rangeからrangeまでとする
){
  start_x *= width / 2.0 / range;
  start_y *= width / 2.0 / range;
  end_x *= width / 2.0 / range;
  end_y *= width / 2.0 / range;
  float arrowLength = 10.0;
  float arrowAngle = 0.4;
  float angle =  atan2(end_y-start_y, end_x-start_x);
  line(start_x, start_y, end_x, end_y);
  pushMatrix();
  translate(end_x, end_y);
  rotate(angle);
  line(0, 0, -arrowLength*cos(arrowAngle), arrowLength*sin(arrowAngle));
  line(0, 0, -arrowLength*cos(arrowAngle), -arrowLength*sin(arrowAngle));
  popMatrix();
}

ソースコード7　pushMatrix 関数と popMatrix 関数との間に line 関数を追記

line 関数は線分を描く関数ですが、pushMatrix 関数と popMatrix 関数との間に追記していますので、やはり直接キャンバス上に描かれるのではなく、透明なシート上に描かれます。今回この2つの line 関数で描く線分は透明なシート上の座標系の中心から$${x}$$軸の負の方向に対して角度 arrowAngle だけ傾いた方向に長さ arrowLength の線分を上下２つ描くことになります。つまり、この透明シート上の2つの線分とキャンバス上にもともと描かれていた線分を組み合わせることで、ベクトルの矢印を描くことができます（図19）。

図19　透明のシート上に2つの線分（青色）を描くイメージ

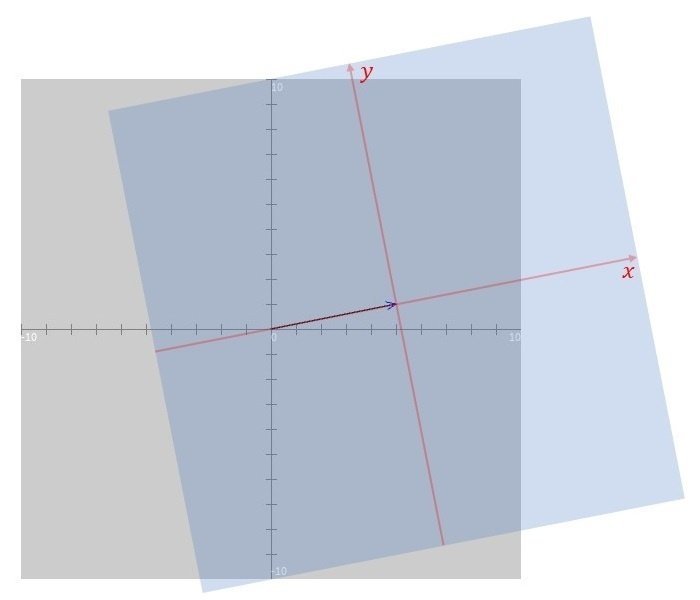
最終的に、透明のシートは見えないので、スケッチ「drawVector」の実行結果としては図1と同じものが得られます。

まとめ

今回はキャンバス上に設定された座標軸を基準としてベクトルを描くための関数を作成し、その利用方法について説明しました。
なお、今回作成したベクトルを描くための関数 arrow についてその解説も行いましたが、『高校数学をプログラミングで解く』でお伝えしたい範囲を超える部分もあります。そのため、最初は関数の詳細にはこだわらず、関数の利用方法だけ知っておいてもらえれば、今後ベクトルを描く際に支障はありませんので、そのまま先の記事に進んでください。

参考文献

Webサイト『Processingで矢印を書く方法（2次元）』

改訂版 教科書傍用 スタンダード 数学B（数研出版、ISBN9784410209468）

Processingをはじめよう 第２版（オライリー・ジャパン、オーム社、ISBN9784873117737）

この記事が気に入ったらサポートをしてみませんか？