高校数学をプログラミングで解く（数学III編）「6-2 平均値の定理」

割引あり

MK's papa

2024年11月27日 05:14

マガジンリスト　＞　数学Ⅲ編 6.微分法の応用　＞　6-2 平均値の定理

はじめに

今回は、数学IIIで学ぶ「平均値の定理」について、平均値の定理の式を満たす$${c}$$の値を計算するプログラムを作成していきます。

平均値の定理

まず、平均値の定理について解説しておきます。

平均値の定理

関数$${f(x)}$$が閉区間$${ [a,b] }$$で連続で、開区間$${ (a,b) }$$で微分可能ならば、

$$
\frac{f(b)-f(a)}{b-a} = f'(c), \ \ \ \ a < c < b
$$

を満たす実数$${c}$$が存在する。
注意　平均値の定理は、次のロルの定理を一般化したもので、曲線$${y = f(x)}$$において、その上の２点$${ \mathrm{A} (a, f(a)), \ \mathrm{B}(b,f(b)) }$$を結ぶ線分に平行な接線が引けるような点$${\mathrm{C}}$$が、曲線上で、$${\mathrm{A}}$$と$${\mathrm{B}}$$の間にあることを意味している。

ロルの定理

（平均値の定理の特別な場合）
関数$${f(x)}$$が閉区間$${ [a,b] }$$で連続で、開区間$${ (a,b) }$$で微分可能で、$${f(a)=f(b)}$$ならば、

$$
f'(c)=0, \ \ \ \ a < c < b
$$

を満たす実数$${c}$$が存在する。

平均値の定理を用いた計算

今回は、平均値の定理の式を満たす$${c}$$の値を計算するプログラムを考えていきます。

問題
次の関数と、示された区間について、平均値の定理の式を満たす$${c}$$の値を求めよ。

$$
y = \sqrt{x} \ \ \ \ [1,9]
$$

アルゴリズム設計

関数$${f(x)}$$に対して、閉区間$${ [a,b] }$$で平均値の定理の式を満たす$${c}$$を求める手順としては以下が考えられます。
① 平均値の定理の左辺の値$${f_c}$$を計算します。

$$
f_c = \frac{f(b)-f(a)}{b-a}
$$

② $${f'(x)}$$を求めて方程式$${f'(x)=f_c}$$を解くと、その解が$${c}$$の候補となるので、$${a < c < b}$$を満たしているかを確かめて、満たしていれば$${c}$$の値とします。

以上の手順で$${c}$$を求めることができますが、今回はこの手順をコンピュータに行わせるので、手順②は以下のように行うことにします。

②’ $${x}$$を$${x=a}$$から$${x=b}$$まで動かして、$${f'(x)=f_c}$$を満たしていれば、そのときの$${x}$$の値を$${c}$$の値とします。

プログラム

それでは、平均値の定理の式を満たす$${c}$$の値を計算するプログラムを作成していきます。

// 平均値の定理の式を満たすcを求めるプログラム
void setup(){

  float a = 1.0; // 区間の下限
  float b = 9.0; // 区間の上限

  // 平均値の定理を満たすcを求める
  float c = calc_c(a,b);
  println("c=", c);

}

// 曲線の関数
float f(
  float x
){
  return sqrt(x);
}

// 曲線の導関数
float f_prime(
  float x
){
  return 1.0/2.0/sqrt(x);
}

// 平均値の定理を満たすcを求める関数
float calc_c(
  float a, // 区間の下限
  float b  // 区間の上限
){
  float c = 1.0;

  // 平均値の左辺の値を計算
  float fc = (f(b)-f(a))/(b-a);

  // 平均値の定理の式を満たすcを求める
  float e = 0.0001;
  float dx = 0.01;
  int n = (int)((b-a)/dx);
  float x;
  for(int i=1; i<n; i++){
    x = a+i*dx;
    if( abs(f_prime(x)-fc) < e ){
      c = x;
    }
  }
  
  return c;
}

ソースコード1　平均値の定理の式を満たす$${c}$$の値を計算するプログラム

ソースコード1で、アルゴリズム設計のところで説明した ②’ について、まず「$${x}$$を$${x=a}$$から$${x=b}$$まで動かして」の部分を変数 dx = 0.01 を用意して、x を a から b まで dx ずつ増やしていくことで実現し、「$${f'(x)=f_c}$$を満たしていれば」の部分を変数 e = 0.0001 を用意して、

abs(f_prime(x)-fc) < e

という条件にして利用しています。

ソースコード1を、Processingの開発環境ウィンドウを開いて（スケッチ名を「calc_mean_value_theorem」としています）、テキストエディタ部分に書いて実行します。

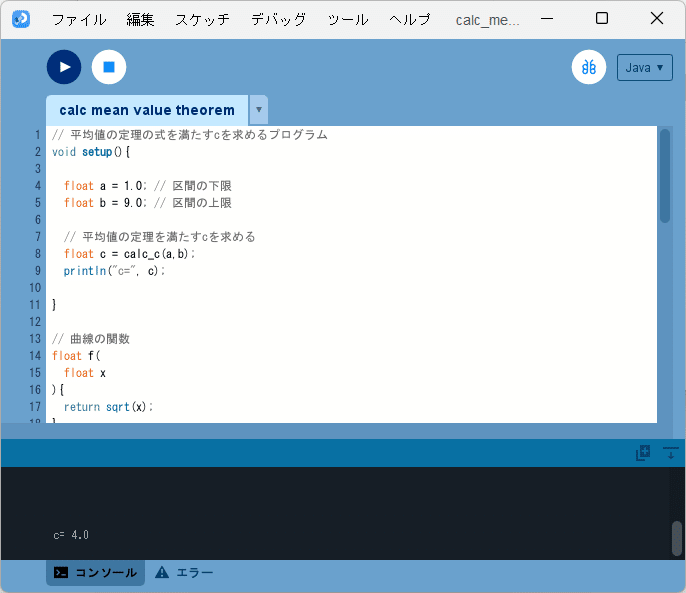
図1のように、開発環境ウィンドウのコンソールに

c= 4.0

と出力されます。この問題では、

$$
f_c = \frac{\sqrt{9}-\sqrt{1}}{9-1}=\frac{1}{4}, \ \ f'(x) = \frac{1}{2 \sqrt{x}}
$$

となりますので、平均値の定理の式を満たす$${c}$$の値は解析的に

$$
c = 4
$$

となります。したがって、プログラムの結果は正しいことがわかります。

おまけ：平均値の定理を図示するプログラム

最後に、スケッチ「calc_mean_value_theorem」で計算した平均値の定理の式を満たす$${c}$$の値を利用して点$${(c,f(c))}$$での接線を描くプログラムを作成します。
今回は、ベースとなるプログラムとして、記事『高校数学をプログラミングで解く（数学II編）「5-2 接線」』で作成したスケッチ「drawTangentialLine」を再利用し、スケッチ「drawTangentialLine」内で記述したプログラムと平均値の定理の式を満たす$${c}$$の値を計算するプログラム（ソースコード1）とを合わせることで作成していきます。以下の zip ファイルをダウンロードして展開または解凍してください。

そして、スケッチの名前（フォルダ名）を「draw_mean_value_theorem」と変更し、またスケッチ「draw_mean_value_theorem」内の「drawTangentialLine.pde」ファイルの名前を「draw_mean_value_theorem.pde」に変更します。そして、pdeファイル「draw_mean_value_theorem.pde」をダブルクリックしてスケッチ「draw_mean_value_theorem」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「draw_mean_value_theorem」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。

float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 5.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500);
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  
  noFill();

  float x_min = -x_range;
  float x_max = x_range;
  
  // 曲線を描く
  stroke(0,0,0);
  draw_curve_function(0.0, x_max);

  float a = 1.0;
  float b = 9.0;
  // (a,f(a)),(b,f(b))をプロットする
  stroke(255,255,0);
  plot_contact_point(a,f(a));
  plot_contact_point(b,f(b));

  // (a,f(a))と(b,f(b))を結ぶ直線を描く
  stroke(0,0,255);
  draw_line_connect_two_points(a,b,x_min,x_max);
  
  // 平均値の定理を満たすcを求める
  float c = calc_c(a,b);
  println("c=", c);

  // (c,f(c))をプロットする
  stroke(0,255,0);
  plot_contact_point(c,f(c));

  // cでの接線を描く
  stroke(255,0,0);
  draw_tangential_line(c,x_min,x_max);

}

// 曲線の関数
float f(
  float x
){
  return sqrt(x);
}

// 曲線の導関数
float f_prime(
  float x
){
  return 1.0/2.0/sqrt(x);
}

// 曲線を描く関数
void draw_curve_function(
  float x_min, // グラフの定義域の下限
  float x_max  // グラフの定義域の上限
){
  int plot_num = 2000; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=1; i<plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // 曲線上の点のx座標
    y = f(x); // 曲線上の点のyの値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

}

// 平均値の定理を満たすcを求める関数
float calc_c(
  float a, // 区間の下限
  float b  // 区間の上限
){
  float c = 1.0;

  // 平均値の左辺の値を計算
  float fc = (f(b)-f(a))/(b-a);

  // 平均値の定理の式を満たすcを求める
  float e = 0.0001;
  float dx = 0.01;
  int n = (int)((b-a)/dx);
  float x;
  for(int i=1; i<n; i++){
    x = a+i*dx;
    if( abs(f_prime(x)-fc) < e ){
      c = x;
    }
  }
  
  return c;
}

// 点cでの接線を描く関数
void draw_tangential_line(
  float c, // 平均値の定理の式を満たすc
  float x_min, // グラフの定義域の下限
  float x_max  // グラフの定義域の上限
){
  int plot_num = 2000; // グラフを描くための頂点の個数  

  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=1; i<plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // 接線上の点のx座標
    y = f_prime(c) * (x-c) + f(c); // 接線上の点のyの値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();
  
}

// (a,f(a))と(b,f(b))を結ぶ直線を描く関数
void draw_line_connect_two_points(
  float a,
  float b,
  float x_min, // グラフの定義域の下限
  float x_max  // グラフの定義域の上限
){
  int plot_num = 2000; // グラフを描くための頂点の個数  
  
  // 直線の傾き
  float fc = (f(b)-f(a))/(b-a);
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=1; i<plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // 直線上の点のx座標
    y = fc * (x-a) + f(a); // 直線上の点のyの値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();
}

// 点をプロットする関数
void plot_contact_point(
  float ax, // 接点のx座標
  float ay  // 接点のy座標
){
  float X, Y; // キャンバス上の座標
  // キャンバス上の座標位置に換算
  X = width / 2.0 / x_range * ax;
  Y = height / 2.0 / y_range * ay;
  strokeWeight(5);
  point(X, Y);
  strokeWeight(1);
}

ソースコード2　平均値の定理の式を満たす$${c}$$での接線を描くプログラム

ソースコード2を、スケッチ「draw_mean_value_theorem」の「draw_mean_value_theorem」タブのテキストエディタ部分に書いて実行すると、図2のように、実行ウィンドウのキャンバス上に、問題の曲線が黒色の線、閉区間の２つの端点$${\mathrm{A}(a,f(a))}$$と$${\mathrm{B}(b,f(b))}$$とを黄色の点、２つの端点を結ぶ直線が青色の線、接点が緑色の点、そして接線が赤色の線でそれぞれ描かれます。

平均値の定理からわかるように、端点を結ぶ直線（青色）と接線（赤色）はお互いに平行になっていることがわかります。

まとめ

今回は、数学IIIで学ぶ「平均値の定理」について、平均値の定理の式を満たす$${c}$$の値を計算するプログラムを作成しました。
平均値の定理の式を満たす$${c}$$の値は、変数$${x}$$を$${a}$$から$${b}$$まで少しずつ変化させながら、条件式

$$
\frac{f(b)-f(a)}{b-a} = f'(x)
$$

に代入していき、条件式が成り立てばそのときの$${x}$$の値を求めたい$${c}$$の値とするように計算しました。このような方法は、コンピュータで関数の最大値、最小値を求めるときなどにも利用してきましたので、比較的理解しやすかったのではないかと思います。

読んだ感想などをお寄せください

本記事を読んだ感想や質問などを以下のお問い合せフォームからお寄せください。感想、質問をいただいた方には本記事の演習問題の解答をプレゼントします。（お問合せフォームの本文に、本記事のタイトルを入れてください。）

参考文献

改訂版教科書傍用スタンダード・オリジナル数学III（数研出版、ISBN9784410209567）

演習問題

次の関数と、示された区間について、平均値の定理の式を満たす$${c}$$の値を求め、点$${(c,f(c))}$$での接線を描くプログラムを作成してください。

$$
y = \cos{x} \ \ \ \ [0,\pi]
$$

ポイント
この演習問題のポイントは、平均値の定理の式を満たす$${c}$$の値が複数あることです。これを考慮して、スケッチ「draw_mean_value_theorem」（ソースコード2）を修正して考えてみてください。

演習問題の解答例

ここから先は

5,423字 / 3画像 / 1ファイル

期間限定！PayPayで支払うと抽選でお得

ログイン

この記事が気に入ったらチップで応援してみませんか？