高校数学をプログラミングで解く（数学B編）「1-3 位置ベクトル」

マガジンリスト　＞　数学B編 1.平面上のベクトル　＞　1-3 位置ベクトル

はじめに

今回は、数学Bで学ぶ「位置ベクトル」について、線分の内分点や外分点、また三角形の重心などの位置ベクトルを計算して、座標上に描くプログラムを作成します。

位置ベクトルと内分点・外分点

まず、位置ベクトルと内分点・外分点についてまとめておきます。なお、$${\mathrm{A} ( \vec{a} )}$$、$${\mathrm{B} ( \vec{b} )}$$、$${\mathrm{C} ( \vec{c} )}$$とします。

① $${ \overrightarrow{ \mathrm{AB} } = \vec{b} - \vec{a} }$$

② 内分点・外分点
線分$${\mathrm{AB}}$$を$${m:n}$$に内分または外分する点について

$$
\mathrm{内分点} \mathrm{P} ( \vec{p} ) : \vec{p} = \frac{n \vec{a} + m \vec{b}}{m+n} \\
\mathrm{外分点} \mathrm{Q} ( \vec{q} ) : \vec{q} = \frac{-n \vec{a} + m \vec{b}}{m-n} \\
\mathrm{中点} \mathrm{M} ( \vec{m} ) : \vec{m} = \frac{ \vec{a} + \vec{b}}{2} 
$$

③ 重心

$$
\triangle \mathrm{ABCの重心} \mathrm{G} ( \vec{g} ) : \vec{g} = \frac{ \vec{a} +  \vec{b} + \vec{c} }{3}
$$

位置ベクトルに関する問題

今回は、下記の問題を解くプログラムを作成していきます。

問題
3つの点$${ \mathrm{A}(\vec{a}) }$$、$${ \mathrm{B}(\vec{b}) }$$、$${ \mathrm{C}(\vec{c}) }$$を

$$
\vec{a} = (2, 3), \ \vec{b} = (5,2), \ \vec{c} = (-2,-7)
$$

とします。このとき、次の点の位置ベクトルをキャンバス上に描け。
(1) 線分$${\mathrm{AB}}$$を$${3:5}$$に内分する点$${ \mathrm{P}_1( \vec{p}_1 ) }$$
(2) 線分$${\mathrm{AB}}$$の中点$${ \mathrm{M}_1( \vec{m}_1 ) }$$
(3) 線分$${\mathrm{AB}}$$を$${3:5}$$に外分する点$${ \mathrm{Q}_1( \vec{q}_1 ) }$$
(4) 線分$${\mathrm{AB}}$$を$${5:3}$$に外分する点$${ \mathrm{Q}_2( \vec{q}_2 ) }$$
(5) $${\triangle \mathrm{ABC}}$$の重心$${ \mathrm{G}( \vec{g} ) }$$

位置ベクトルを描くプログラム

今回の問題は位置ベクトルと内分点・外分点や重心の定義通りにプログラムを作成していくだけです。記事『高校数学をプログラミングで解く（数学B編）「1-1 ベクトルの演算」』で説明したPVectorクラスのベクトルについての和や実数倍などを利用して、比較的簡単に作成することができますが、多少組合せの仕方が複雑でもあるので、注意が必要です。
記事『高校数学をプログラミングで解く（数学B編）「1-0 ベクトルを描く」』で作成したスケッチ「drawVector」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「drawPositionVector」と変更し、またスケッチ「drawPositionVector」内の「drawVector.pde」ファイルの名前を「drawPositionVector.pde」に変更します。そして、pdeファイル「drawPositionVector.pde」をダブルクリックしてスケッチ「drawPositionVector」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「drawPositionVector」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。

// 位置ベクトルを描く
void setup(){
  size(500,500,P2D);
  noLoop();
  float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
  float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで 
  setAxes(x_range, y_range); // 座標軸の準備

  PVector a = new PVector(2.0, 3.0);
  PVector b = new PVector(5.0, 2.0);
  PVector c = new PVector(-2.0, -7.0);
  
  float m = 3.0;
  float n = 5.0;
  
  // (1) 線分ABをm:nに内分する点
  PVector p1 = a.copy().mult(n).add( b.copy().mult(m) ).mult(1.0/(m+n));
  
  // (2) 線分ABの中点
  PVector m1 = a.copy().add(b.copy()).mult(1.0/2.0);
 
  // (3) 線分ABをm:nに外分する点
  PVector q1 = a.copy().mult(-n).add( b.copy().mult(m) ).mult(1.0/(m-n));
 
  // (4) 線分ABをn:mに外分する点
  PVector q2 = a.copy().mult(-m).add( b.copy().mult(n) ).mult(1.0/(n-m));
 
  // (5) △ABCの重心
  PVector g = a.copy().add( b.copy() ).add( c.copy() ).mult(1.0/3.0);
 println(g);
  // 以下にグラフを描いていく
  noFill(); // グラフの中身を塗りつぶさない
  stroke(0,0,0); // グラフの線の色を黒色に設定

  // キャンバスにベクトルを描画
  arrow(0.0, 0.0, a.x, a.y, x_range);
  arrow(0.0, 0.0, b.x, b.y, x_range);
  arrow(0.0, 0.0, c.x, c.y, x_range);
 
  // (1)の位置ベクトルを赤色で描く
  stroke(255,0,0);
  arrow(0.0, 0.0, p1.x, p1.y, x_range);

  // (2)の位置ベクトルを青色で描く  
  stroke(0,0,255);
  arrow(0.0, 0.0, m1.x, m1.y, x_range);

  // (3)(4)の位置ベクトルを緑色で描く
  stroke(0,255,0);
  arrow(0.0, 0.0, q1.x, q1.y, x_range);
  arrow(0.0, 0.0, q2.x, q2.y, x_range);
 
  // (5)の位置ベクトルを水色で描く
  stroke(0,255,255);
  arrow(0.0, 0.0, g.x, g.y, x_range);
  
}

ソースコード1　位置ベクトルを描くプログラム

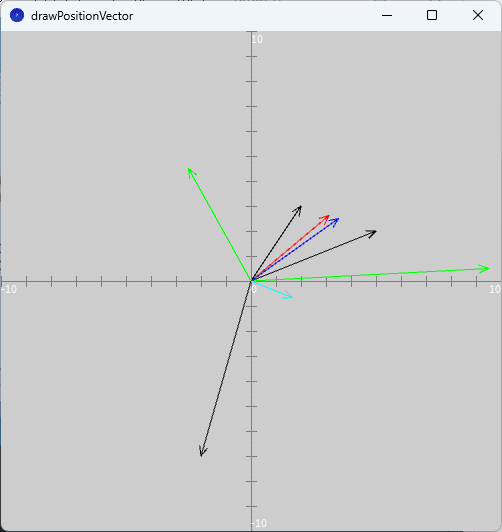
このスケッチ「drawPositionVector」を実行すると、図1のように、実行ウィンドウのキャンバスにそれぞれの位置ベクトルが矢印で描かれます。

図1　位置ベクトルの描画

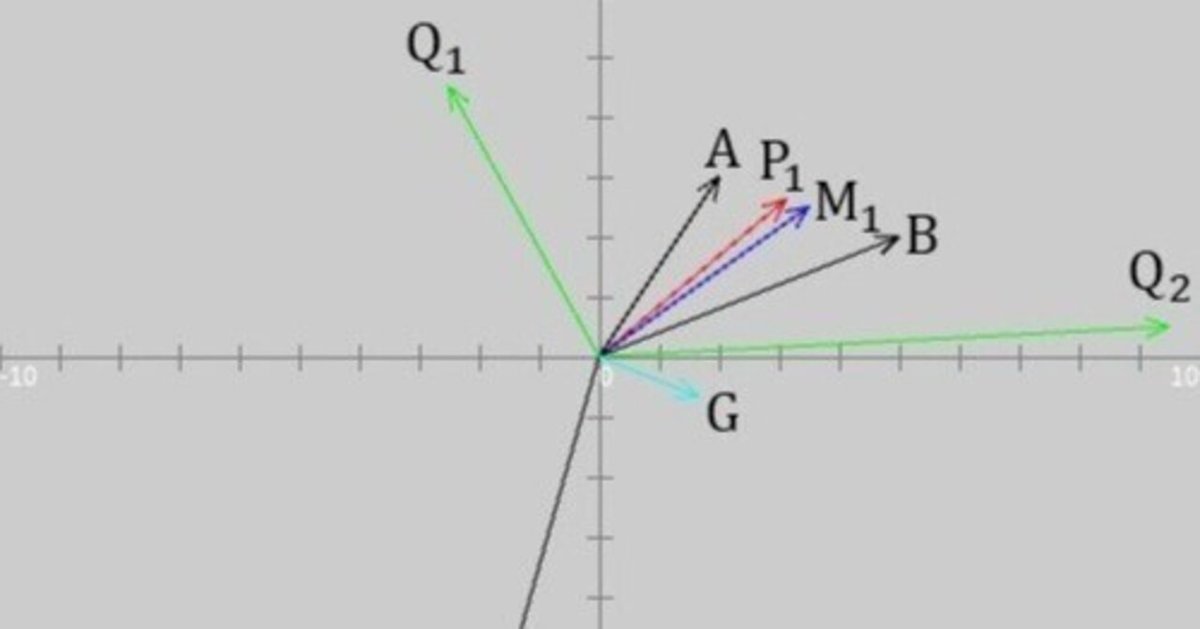
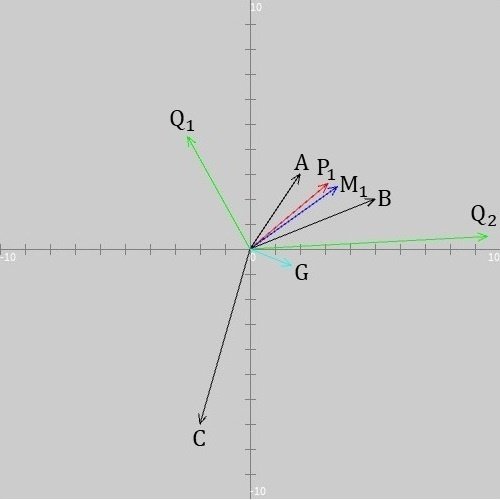
念のため、それぞれの位置ベクトルのラベルを張ったものを示しておきます。

図2　位置ベクトル（ラベル付き）

まとめ

今回は、数学Bで学ぶ「位置ベクトル」について、線分の内分点や外分点、また三角形の重心などの位置ベクトルを計算して、座標上に描くプログラムを作成しました。
位置ベクトルの計算は、PVectorクラスを利用して準備したベクトルをコピーし、PVectorクラスの和や実数倍の関数を利用して計算しますが、多少演算が複雑になりますので、一つ一つ正しい組み合わせになっているかを確かめながら作成していくとよいでしょう。
位置ベクトルを計算したら、あとは arrow 関数を用いて描画していけばよいだけですので、このあたりは簡単だったのではないでしょうか。
位置ベクトルの概念は今後も重要になっていくので、プログラミングを行うことでより理解を深めていってください。

参考文献

改訂版 教科書傍用 スタンダード 数学B（数研出版、ISBN9784410209468）