
高校数学をプログラミングで解く(数学III編)「2-5 2次曲線と直線」
マガジンリスト > 数学Ⅲ編 2.式と曲線 > 2-5 2次曲線と直線
はじめに
今回は、数学IIIで学ぶ「2次曲線と直線」について、2次曲線の接線を描くプログラムを作成します。
2次曲線と直線、2次曲線と接線
まず、2次曲線と直線の関係、および2次曲線と接線の関係について解説します。
2次曲線と直線
① 共有点の座標
2次曲線と直線の方程式を連立させたときの実数解
②位置関係
①の方程式から1変数を消去してできる2次方程式の判別式$${D}$$
$$
\begin{array}{rcl}
\mathrm{2点で交わる} & \Leftrightarrow & D > 0 \\
\mathrm{接する} & \Leftrightarrow & D = 0 \\
\mathrm{共有点がない} & \Leftrightarrow & D < 0
\end{array}
$$
注意
放物線と直線(軸に平行)、双曲線と直線(漸近線に平行)の場合、1変数を消去すると1次方程式になる。そのときは1点で交わる。
2次曲線と接線
2次曲線上の点$${(x_1,y_1)}$$における接線の方程式
① 放物線
$$
y^2 = 4px
$$
の接線は
$$
y_1y = 2p(x+x_1) \ \ [ y_1^2 = 4px_1 ]
$$
② 楕円
$$
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1
$$
の接線は
$$
\frac{x_1x}{a^2} + \frac{y_1y}{b^2} = 1 \ \ \left[ \frac{x_1^2}{a^2}+\frac{y_1^2}{b^2} = 1 \right]
$$
③ 双曲線
$$
\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1
$$
の接線は
$$
\frac{x_1x}{a^2} - \frac{y_1y}{b^2} = 1 \ \ \left[ \frac{x_1^2}{a^2}-\frac{y_1^2}{b^2} = 1 \right]
$$
2次曲線と接線を描くプログラム
今回は、上記で説明した各2次曲線の接線の方程式を用いて、実際に接線を描くプログラムを作成していきます。
なお、接線の方程式は以下のように$${y=f(x)}$$の形に書き換えて利用していきます。
① 放物線の接線の方程式
$$
y= \frac{2p}{y_1} (x+x_1)
$$
② 楕円の接線の方程式
$$
y = \left( 1-\frac{x_1x}{a^2} \right) \cdot \frac{b^2}{y_1}
$$
③ 双曲線の接線の方程式
$$
y = \left( \frac{x_1x}{a^2} - 1 \right) \cdot \frac{b^2}{y_1}
$$
放物線の接線を描くプログラム
今回は、$${x}$$軸を軸とする放物線
$$
y^2 = 4 \cdot 2 x
$$
上の点$${(2,4)}$$での接線を描くプログラムを作成します。
記事『高校数学をプログラミングで解く(数学III編)「2-1 放物線」』で作成したスケッチ「draw_parabola」において、$${x}$$軸を軸とする放物線を描く関数 draw_parabola_x_axis を準備しているので、これらを再利用します。以下の zip ファイルをダウンロードして展開または解凍してください。
そして、スケッチの名前(フォルダ名)を「draw_parabola_w_tangent」と変更し、またスケッチ「draw_parabola_w_tangent」内の「draw_parabola.pde」ファイルの名前を「draw_parabola_w_tangent.pde」に変更します。そして、pdeファイル「draw_parabola_w_tangent.pde」をダブルクリックしてスケッチ「draw_parabola_w_tangent」の開発環境ウィンドウを立ち上げます。そして、開発環境ウィンドウのタブ欄で「draw_parabola_w_tangent」タブを選択して、そのテキストエリアのソースコードを以下のソースコード1に書き換えます。
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500);
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill();
stroke(0,0,0);
// 焦点が(2,0)、準線がx=-2の放物線
float p = 2.0;
float a = 0.0;
float b = 0.0;
stroke(255,0,0);
draw_parabola_x_axis(p,a,b);
// 点(2,4)での接線
float x1 = 2.0;
float y1 = 4.0;
stroke(0,0,255);
tangent_line_of_parabola(p,x1,y1);
// 接点をプロット
stroke(0,0,0);
plot_point(x1,y1);
}
// x軸を軸とする放物線を描く関数
void draw_parabola_x_axis(
float p, // 焦点(p,0)、準線x=-p
float a, // x軸方向の平行移動
float b // y軸方向の平行移動
){
// グラフの定義域
float y_min = -y_range;
float y_max = y_range;
int plot_num = 200; // グラフを描くための頂点の個数
// グラフを描画
float x, y; // 関数の座標
float X, Y; // キャンバス上の座標
beginShape();
for(int i=0; i<=plot_num; i++){
y = y_min + (y_max - y_min) / plot_num * i; // 放物線上の点のy座標
x = (y-b)*(y-b)/4.0/p+a; // 放物線上の点のx座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
// 焦点をプロット
x = p + a;
y = b;
plot_point(x,y);
// 準線を描く
x = -p + a;
X = width / 2.0 / x_range * x;
line(X, -height/2.0, X, height);
}
// y軸を軸とする放物線を描く関数
void draw_parabola_y_axis(
float q, // 焦点(0,q)、準線x=-q
float a, // x軸方向の平行移動
float b // y軸方向の平行移動
){
// グラフの定義域
float x_min = -x_range;
float x_max = x_range;
int plot_num = 200; // グラフを描くための頂点の個数
// グラフを描画
float x, y; // 関数の座標
float X, Y; // キャンバス上の座標
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_min + (x_max - x_min) / plot_num * i; // 放物線上の点のx座標
y = (x-a)*(x-a)/4.0/q+b; // 放物線上の点のy座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
// 焦点をプロット
x = a;
y = q + b;
plot_point(x,y);
// 準線を描く
y = -q + b;
Y = height / 2.0 / y_range * y;
line(-width/2.0, Y, width/2.0, Y);
}
// 座標(x,y)に点をプロットする関数
void plot_point(
float x, // 点のx座標
float y // 点のy座標
){
float X, Y; // キャンバス上の座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
strokeWeight(5);
point(X, Y);
strokeWeight(1);
}
// x軸を軸とする放物線の接線を描く関数
void tangent_line_of_parabola(
float p, // 放物線の焦点(p,0)、準線x=-p
float x1, // 接点のx座標
float y1 // 接点のy座標
){
float xl, yl;
float xr, yr;
// 接線の左端の点
xl = -x_range;
yl = 2.0 * p * (xl + x1)/y1;
// 接線の右端の点
xr = x_range;
yr = 2.0 * p * (xr + x1)/y1;
// キャンバスの座標系に変換
float Xl, Yl;
float Xr, Yr;
Xl = width / 2.0 / x_range * xl;
Yl = height / 2.0 / y_range * yl;
Xr = width / 2.0 / x_range * xr;
Yr = height / 2.0 / y_range * yr;
// 接線を描画
line(Xl, Yl, Xr, Yr);
}ソースコード1 放物線の接線を描くプログラム
ソースコード1は、基本的にスケッチ「draw_parabola」で作成したソースコードに接線を描くための関数 tangent_line_of_parabola を追加して、setup 関数内で呼び出しているだけです。tangent_line_of_parabola 関数については、放物線の接線の方程式がわかっているので、それを利用して$${x}$$軸の描画範囲内一杯に接線が描かれるように準備しています。
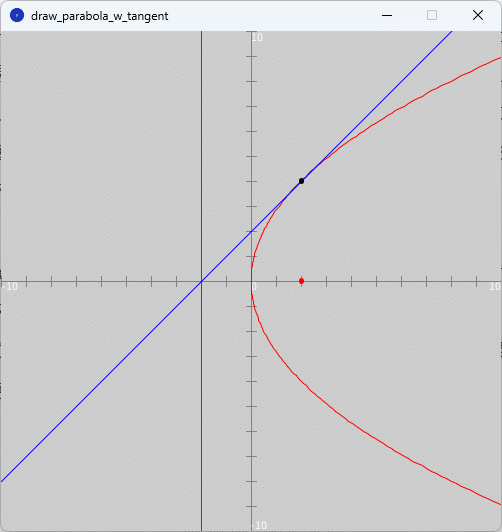
「draw_parabola_w_tangent」タブのテキストエリアをソースコード1に書き換えて、スケッチ「draw_parabola_w_tangent」を実行すると、図1のように、実行ウィンドウのキャンバス上に放物線が赤色、放物線の接線が青色、接点が黒色で描かれます。
楕円の接線を描くプログラム
次に、$${a=4, b=3}$$の楕円上の点$${(x_1, y_1)}$$(ここで$${x_1=2}$$で、$${y_1 > 0}$$)での接線を描くプログラムを作成します。
記事『高校数学をプログラミングで解く(数学III編)「2-2 楕円」』で作成したスケッチ「draw_ellipse」において、中心を原点、焦点を$${x}$$軸または$${y}$$軸上とする楕円を描く関数 draw_ellipse_w_focuses を準備しているので、これらを再利用します。以下の zip ファイルをダウンロードして展開または解凍してください。
スケッチの名前(フォルダ名)を「draw_ellipse_w_tangent」と変更し、またスケッチ「draw_ellipse_w_tangent」内の「draw_ellipse.pde」ファイルの名前を「draw_ellipse_w_tangent.pde」に変更します。そして、pdeファイル「draw_ellipse_w_tangent.pde」をダブルクリックしてスケッチ「draw_ellipse_w_tangent」の開発環境ウィンドウを立ち上げます。そして、開発環境ウィンドウのタブ欄で「draw_ellipse_w_tangent」タブを選択して、そのテキストエリアのソースコードを以下のソースコード2に書き換えます。
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500);
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill();
stroke(0,0,0);
// a=4,b=3の楕円
float a = 4.0;
float b = 3.0;
stroke(255,0,0);
draw_ellipse_w_focuses(a,b);
// x1=2, y1>0での接線
float x1 = 2.0;
float y1 = sqrt(1.0-x1*x1/a/a) * b;
stroke(0,0,255);
tangent_line_of_ellipse(a,b,x1,y1);
// 接点をプロット
stroke(0,0,0);
plot_point(x1,y1);
}
// 中心を原点、焦点をx軸またはy軸上とする楕円を描く関数
void draw_ellipse_w_focuses(
float a, // 楕円の幅の半分
float b // 楕円の高さの半分
){
// グラフを描画
float A, B; // キャンバス上での軸の長さ
A = width / 2.0 / x_range * a;
B = height / 2.0 / y_range * b;
ellipse(0.0,0.0,2.0*A,2.0*B);
// 焦点を描画
if(a > b){ // x軸方向に長軸がある場合
plot_point(sqrt(a*a-b*b),0.0);
plot_point(-sqrt(a*a-b*b),0.0);
} else if(a < b){ // y軸方向に長軸がある場合
plot_point(0.0,sqrt(b*b-a*a));
plot_point(0.0,-sqrt(b*b-a*a));
} else { // 円の場合
plot_point(0.0,0.0);
}
}
// 座標(x,y)に点をプロットする関数
void plot_point(
float x, // 点のx座標
float y // 点のy座標
){
float X, Y; // キャンバス上の座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
strokeWeight(5);
point(X, Y);
strokeWeight(1);
}
// 中心を原点、焦点をx軸またはy軸上とする楕円の接線を描く関数
void tangent_line_of_ellipse(
float a, // 楕円の幅の半分
float b, // 楕円の高さの半分
float x1, // 接点のx座標
float y1 // 接点のy座標
){
float xl, yl;
float xr, yr;
// 接線の左端の点
xl = -x_range;
yl = (1.0 - x1*xl/a/a) * b*b/y1;
// 接線の右端の点
xr = x_range;
yr = (1.0 - x1*xr/a/a) * b*b/y1;
// キャンバスの座標系に変換
float Xl, Yl;
float Xr, Yr;
Xl = width / 2.0 / x_range * xl;
Yl = height / 2.0 / y_range * yl;
Xr = width / 2.0 / x_range * xr;
Yr = height / 2.0 / y_range * yr;
// 接線を描画
line(Xl, Yl, Xr, Yr);
}ソースコード2 楕円の接線を描くプログラム
ソースコード2は、基本的にスケッチ「draw_ellipse」で作成したソースコードに接線を描くために関数 tangent_line_of_ellipse を追加して、setup 関数内で呼び出しているだけです。tangent_line_of_ellipse 関数についても、楕円の接線の方程式がわかっているので、それを利用して$${x}$$軸の描画範囲内一杯に接線が描かれるように準備しています。
「draw_ellipse_w_tangent」タブのテキストエリアをソースコード2に書き換えて、スケッチ「draw_ellipse_w_tangent」を実行すると、図2のように、実行ウィンドウのキャンバス上に楕円が赤色、楕円の接線が青色、接点が黒色で描かれます。

双曲線の接線を描くプログラム
最後に、$${a=4, b=3}$$の双曲線上の点$${(x_1, y_1)}$$(ここで$${x_1=5}$$で、$${y_1 > 0}$$)での接線を描くプログラムを作成します。
記事『高校数学をプログラミングで解く(数学III編)「2-3 双曲線」』で作成したスケッチ「draw_hyperbola」において、焦点が$${x}$$軸上にある双曲線を描く関数 draw_hyperbola_x_axis を準備しているので、これらを再利用します。以下の zip ファイルをダウンロードして展開または解凍してください。
スケッチの名前(フォルダ名)を「draw_hyperbola_w_tangent」と変更し、またスケッチ「draw_hyperbola_w_tangent」内の「draw_hyperbola.pde」ファイルの名前を「draw_hyperbola_w_tangent.pde」に変更します。そして、pdeファイル「draw_hyperbola_w_tangent.pde」をダブルクリックしてスケッチ「draw_hyperbola_w_tangent」の開発環境ウィンドウを立ち上げます。そして、開発環境ウィンドウのタブ欄で「draw_hyperbola_w_tangent」タブを選択して、そのテキストエリアのソースコードを以下のソースコード3に書き換えます。
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで
void setup(){
size(500,500);
noLoop();
setAxes(x_range, y_range); // 座標軸の準備
noFill();
stroke(0,0,0);
float a,b; // 双曲線の係数
stroke(255,0,0);
// a=4,b=3の双曲線
a = 4.0;
b = 3.0;
draw_hyperbola_x_axis(a,b);
// x1=5, y1>0での接線
float x1 = 5.0;
float y1 = sqrt(x1*x1/a/a-1.0) * b;
stroke(0,0,255);
tangent_line_of_hyperbola(a,b,x1,y1);
// 接点をプロット
stroke(0,0,0);
plot_point(x1,y1);
}
// 焦点がx軸上にある双曲線を描く関数
void draw_hyperbola_x_axis(
float a, // x^2の係数
float b // y^2の係数
){
// グラフの定義域
float y_min = -y_range;
float y_max = y_range;
int plot_num = 200; // グラフを描くための頂点の個数
// グラフを描画
float x, y; // 関数の座標
float X, Y; // キャンバス上の座標
// x>0の双曲線
beginShape();
for(int i=0; i<=plot_num; i++){
y = y_min + (y_max - y_min) / plot_num * i; // 双曲線上の点のy座標
x = a * sqrt(y*y/b/b+1.0); // 双曲線上の点のx座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
// x<0の双曲線
beginShape();
for(int i=0; i<=plot_num; i++){
y = y_min + (y_max - y_min) / plot_num * i; // 双曲線上の点のy座標
x = -a * sqrt(y*y/b/b+1.0); // 双曲線上の点のx座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
// 焦点をプロット
x = sqrt(a*a+b*b);
y = 0.0;
plot_point(x,y);
plot_point(-x,y);
// 漸近線を描く
x = x_range;
y = b * x / a;
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
line(-X, -Y, X, Y);
line(-X, Y, X, -Y);
}
// 焦点がy軸上にある双曲線を描く関数
void draw_hyperbola_y_axis(
float a, // x^2の係数
float b // y^2の係数
){
// グラフの定義域
float x_min = -x_range;
float x_max = x_range;
int plot_num = 200; // グラフを描くための頂点の個数
// グラフを描画
float x, y; // 関数の座標
float X, Y; // キャンバス上の座標
// y>0の双曲線
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_min + (x_max - x_min) / plot_num * i; // 双曲線上の点のx座標
y = b * sqrt(x*x/a/a+1.0); // 双曲線上の点のy座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
// y<0の双曲線
beginShape();
for(int i=0; i<=plot_num; i++){
x = x_min + (x_max - x_min) / plot_num * i; // 双曲線上の点のx座標
y = -b * sqrt(x*x/a/a+1.0); // 双曲線上の点のy座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
vertex(X, Y);
}
endShape();
// 焦点をプロット
x = 0.0;
y = sqrt(a*a+b*b);
plot_point(x,y);
plot_point(x,-y);
// 漸近線を描く
x = x_range;
y = b * x / a;
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
line(-X, -Y, X, Y);
line(-X, Y, X, -Y);
}
// 座標(x,y)に点をプロットする関数
void plot_point(
float x, // 点のx座標
float y // 点のy座標
){
float X, Y; // キャンバス上の座標
// キャンバス上の座標位置に換算
X = width / 2.0 / x_range * x;
Y = height / 2.0 / y_range * y;
strokeWeight(5);
point(X, Y);
strokeWeight(1);
}
// 焦点がx軸上にある双曲線の接線を描く関数
void tangent_line_of_hyperbola(
float a, // x^2の係数
float b, // y^2の係数
float x1, // 接点のx座標
float y1 // 接点のy座標
){
float xl, yl;
float xr, yr;
// 接線の左端の点
xl = -x_range;
yl = (x1*xl/a/a - 1.0) * b*b/y1;
// 接線の右端の点
xr = x_range;
yr = (x1*xr/a/a - 1.0) * b*b/y1;
// キャンバスの座標系に変換
float Xl, Yl;
float Xr, Yr;
Xl = width / 2.0 / x_range * xl;
Yl = height / 2.0 / y_range * yl;
Xr = width / 2.0 / x_range * xr;
Yr = height / 2.0 / y_range * yr;
// 接線を描画
line(Xl, Yl, Xr, Yr);
}
ソースコード3 双曲線の接線を描くプログラム
ソースコード3は、基本的にスケッチ「draw_hyperbola」で作成したソースコードに接線を描くために関数 tangent_line_of_hyperbola を追加して、setup 関数内で呼び出しているだけです。tangent_line_of_hyperbola 関数についても、双曲線の接線の方程式がわかっているので、それを利用して$${x}$$軸の描画範囲内一杯に接線が描かれるように準備しています。
「draw_hyperbola_w_tangent」タブのテキストエリアをソースコード3に書き換えて、スケッチ「draw_hyperbola_w_tangent」を実行すると、図3のように、実行ウィンドウのキャンバス上に双曲線が赤色、双曲線の接線が青色、接点が黒色で描かれます。

まとめ
今回は、数学IIIで学ぶ「2次曲線と直線」について、2次曲線の接線を描くプログラムを作成しました。
$${x}$$軸上に2次曲線の中心や焦点が乗っている場合、接線の方程式は比較的簡単な形で与えられ、それらの方程式を用いて接線を描くプログラムを作成しました。
より一般的な2次曲線に対しても接線を描くことは可能です。例えば、一般的な2次曲線を一旦$${x}$$軸上に中心や焦点が乗っている2次曲線となるように平行移動、回転移動したあと、それに対して接線を描き、再度接線と一緒に一般的な2次曲線に戻す、という方法が考えられます。是非チャレンジしてみてください。
また、今回作成したプログラムでは、$${y_1=0}$$の場合を除いた形で作成しています。$${y_1=0}$$の場合も接線を描くことができるようにすることは比較的簡単ですので、こちらも実装してみてください。
参考文献
改訂版 教科書傍用 スタンダード・オリジナル 数学III(数研出版、ISBN9784410209567)
演習問題
点$${(0,2)}$$から楕円$${x^2+4y^2=4}$$に引いた接線の方程式を求めて、その接線をキャンバス上に描くプログラムを作成してください。
演習問題の解答例
ここから先は
Amazonギフトカード5,000円分が当たる
この記事が気に入ったらチップで応援してみませんか?
