高校数学をプログラミングで解く（数学III編）「2-10 極方程式」

割引あり

MK's papa

2024年10月9日 06:16

マガジンリスト　＞　数学Ⅲ編 2.式と曲線　＞　2-10 極方程式

はじめに

今回は、数学IIIで学ぶ「極方程式」について、極方程式を利用して円、直線、および２次曲線を描くプログラムを作成します。

極方程式

まず、極方程式について解説します。

円の極方程式

[1] 中心が極、半径が$${a}$$　$${\Rightarrow}$$　$${r=a}$$
[2] 中心の極座標が$${(a,0)}$$、半径が$${a}$$　$${\Rightarrow}$$　$${r=2a \cos \theta}$$

直線の極方程式

[1] 極$${\mathrm{O}}$$を通り、始線とのなす角が$${\alpha}$$　$${\Rightarrow}$$　$${\theta=\alpha}$$
[2] 極座標が$${(a, \alpha)}$$である点$${\mathrm{A}}$$を通り、$${\mathrm{OA}}$$に垂直（$${\mathrm{O}}$$は極）

$$
r \cos (\theta - \alpha) = a \ \ (a > 0)
$$

２次曲線の極方程式

極座標が$${(a,0)}$$である点$${A}$$を通り、始線$${\mathrm{OX}}$$に垂直な直線を$${l}$$とする。離心率$${e}$$の２次曲線の極方程式は

$$
r = \frac{ea}{1+e \cos \theta}
$$

[1] $${0 < e <1}$$のとき、$${\mathrm{O}}$$を焦点の１つとする楕円
[2] $${e=1}$$のとき、$${\mathrm{O}}$$を焦点、$${l}$$を準線とする放物線
[3] $${e > 1}$$のとき、$${\mathrm{O}}$$を焦点の１つとする双曲線

参考：2次曲線の極方程式と直交座標との関係

上記の２次曲線の極方程式を$${x=r\cos \theta, \ y=r \sin \theta}$$の関係式を利用して直交座標系の方程式に変換してみます。

[1] 楕円

$$
\frac{(x-\Delta x)^2}{p^2} + \frac{y^2}{q^2} = 1 \ \ \left( \ p=\frac{ea}{1-e^2}, \ q=\frac{ea}{\sqrt{1-e^2}}, \ \Delta x = -\frac{e^2a}{1-e^2} \right)
$$

[2] 放物線

$$
y^2 = 4p(x-\Delta x) \ \ \left( p = -\frac{a}{2}, \ \Delta x = \frac{a}{2} \right)
$$

[3] 双曲線

$$
\frac{(x-\Delta x)^2}{p^2} - \frac{y^2}{q^2} = 1 \ \ \left( \ p=\frac{ea}{e^2-1}, \ q=\frac{ea}{\sqrt{e^2-1}}, \ \Delta x = \frac{e^2a}{e^2-1} \right)
$$

以下では、これらの極方程式を用いてそれぞれの曲線を描くプログラムを作成していきます。

極方程式を用いた円の描画

まず、極方程式を用いて円を描くプログラムを考えていきます。

アルゴリズム設計

円の極方程式[1]の場合、動径$${r}$$が$${a}$$に固定されますので、あとは偏角$${\theta}$$を$${0}$$から$${2 \pi}$$まで動かしながら、

$$
x = a \cos \theta, \ \ y = a \sin \theta
$$

と、極座標から直交座標に変換した上で、点$${(x,y)}$$を順に結んでいくことで、円を描くことができます。
円の極方程式[2]の場合、動径$${r}$$が偏角$${\theta}$$に依存しますので、偏角$${\theta}$$を$${0}$$から$${2 \pi}$$まで動かしながら、

$$
r=2a \cos \theta
$$

で動径$${r}$$の大きさを決定したあと、極座標から直交座標に変換した上で、点$${(x,y)}$$を順に結んでいくことで、円を描くことができます。ただし、１点注意が必要です。動径$${r}$$は$${0}$$以上の値になりますので、$${ \cos \theta < 0}$$となるような$${\theta}$$の領域では円の極方程式[2]を利用することができません。そのため、今回のプログラムでは、$${ r \geq 0}$$となるような$${r}$$の領域でのみ点を描くようにします。

プログラム

極方程式を用いて円を描くプログラムを作成するにあたり、記事『高校数学をプログラミングで解く（数学III編）「2-8 曲線の媒介変数表示」』で作成したスケッチ「draw_ellipse_parameter」を再利用します。以下の zip ファイルをダウンロードして展開または解凍してください。

そして、スケッチの名前（フォルダ名）を「draw_circle_polor_equation」と変更し、またスケッチ「draw_circle_polor_equation」内の「draw_ellipse_parameter.pde」ファイルの名前を「draw_circle_polor_equation.pde」に変更します。そして、pdeファイル「draw_circle_polor_equation.pde」をダブルクリックしてスケッチ「draw_circle_polor_equation」の開発環境ウィンドウを立ち上げます。そして、開発環境ウィンドウのタブ欄で「draw_circle_polor_equation」タブを選択して、そのテキストエリアのソースコードを以下のソースコード1に書き換えます。

float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500);
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  
  noFill();
  stroke(0,0,0);

  float a = 3.0;
  stroke(255,0,0);
  draw_circle_polor1(a);
  
  stroke(0,0,255);
  draw_circle_polor2(a);

}

// 中心が極、半径がaの円を極方程式で描く
void draw_circle_polor1(
  float a // 円の半径
){

  // グラフを描画
  int plot_num = 2000; // グラフを描くための頂点の最大個数  
  
  float r, theta; // 極座標
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<=plot_num; i++){
    theta = 2.0 * PI / plot_num * i;
    r = a;
    x = r * cos(theta);
    y = r * sin(theta);

    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();
  
  // 中心をプロット
  plot_point(0.0,0.0);

}

// 中心の極座標が(a,0)、半径がaの円を極方程式で描く
void draw_circle_polor2(
  float a // 円の半径
){

  // グラフを描画
  int plot_num = 2000; // グラフを描くための頂点の最大個数  
  
  float r, theta; // 極座標
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<=plot_num; i++){
    theta = 2.0 * PI / plot_num * i;
    r = 2.0 * a * cos(theta);
    if(r >= 0){
      x = r * cos(theta);
      y = r * sin(theta);

      // キャンバス上の座標位置に換算
      X = width / 2.0 / x_range * x;
      Y = height / 2.0 / y_range * y;
      vertex(X, Y);
    }
  }
  endShape();
  
  // 中心をプロット
  plot_point(a,0.0);

}

// 座標(x,y)に点をプロットする関数
void plot_point(
  float x, // 点のx座標
  float y  // 点のy座標
){
  float X, Y; // キャンバス上の座標
  // キャンバス上の座標位置に換算
  X = width / 2.0 / x_range * x;
  Y = height / 2.0 / y_range * y;
  strokeWeight(5);
  point(X, Y);
  strokeWeight(1);
}

ソースコード1　極方程式を用いて円を描くプログラム

ソースコード1では、円の極方程式[1]を用いて円を描く関数を　draw_circle_polor1 とし、円の極方程式[2]を用いて円を描く関数を　draw_circle_polor2 として準備して setup 関数内で利用するようにしています。

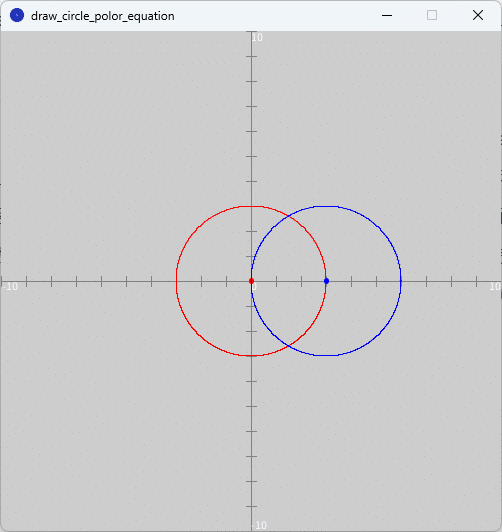
スケッチ「draw_circle_polor_equation」の「draw_circle_polor_equation」タブを選択してそのテキストエディタ部分をソースコード1で書き換えて実行すると、図1のように、実行ウィンドウのキャンバスの$${xy}$$平面上に、円の極方程式[1]による円が赤色、円の極方程式[2]による円が青色でそれぞれ描かれます。なお、円の半径$${a}$$はともに$${a=3}$$として描いています。

極方程式を用いた直線の描画

次に、極方程式を用いて直線を描くプログラムを考えていきます。

アルゴリズム設計

直線の極方程式[1]の場合、偏角$${\theta}$$が$${\alpha}$$に固定されますので、あとは動径$${r}$$を$${0}$$から$${r_{\mathrm{max}}}$$まで動かしながら、

$$
x = r \cos \alpha, \ \ y = r \sin \alpha
$$

と、極座標から直交座標に変換した上で、点$${(x,y)}$$を順に結んでいくことで、直線を描くことができます。
直線の極方程式[2]の場合、動径$${r}$$が偏角$${\theta}$$に依存しますので、偏角$${\theta}$$を$${0}$$から$${2 \pi}$$まで動かしながら、

$$
r= \frac{a}{ \cos (\theta - \alpha) }
$$

で動径$${r}$$の大きさを決定したあと、極座標から直交座標に変換した上で、点$${(x,y)}$$を順に結んでいくことで、直線を描くことができます。ただし、円の極方程式のときと同様、注意が必要です。動径$${r}$$は$${0}$$以上の値になりますので、$${ \cos (\theta - \alpha) \leq 0}$$となるような$${\theta}$$の領域では直線の極方程式[2]を利用することができません。そのため、今回のプログラムでは、$${ \cos (\theta - \alpha) > 0}$$となるような$${\theta}$$の領域でのみ点を描くようにします。

プログラム

極方程式を用いて直線を描くプログラムを作成するにあたり、上記で作成したスケッチ「draw_circle_polor_equation」を再利用します。
スケッチ「draw_circle_polor_equation」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「draw_line_polor_equation」と変更し、またスケッチ「draw_line_polor_equation」内の「draw_circle_polor_equation.pde」ファイルの名前を「draw_line_polor_equation.pde」に変更します。そして、pdeファイル「draw_line_polor_equation.pde」をダブルクリックしてスケッチ「draw_line_polor_equation」の開発環境ウィンドウを立ち上げます。そして、開発環境ウィンドウのタブ欄で「draw_line_polor_equation」タブを選択して、そのテキストエリアのソースコードを以下のソースコード2に書き換えます。

float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500);
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  
  noFill();
  stroke(0,0,0);

  float alpha = PI/3.0;
  stroke(255,0,0);
  draw_line_polor1(alpha);
  
  float a = 3.0;
  stroke(0,0,255);
  draw_line_polor2(a,alpha);

}

// 極Ｏを通り、始線とのなす角がalphaの直線を極方程式で描く
void draw_line_polor1(
  float alpha // 始線とのなす角
){

  // グラフを描画
  int plot_num = 2000; // グラフを描くための頂点の最大個数
  float r_max = 2.0 * sqrt(2.0) * x_range; // 動径rの最大値を設定
  
  float r, theta; // 極座標
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<=plot_num; i++){
    theta = alpha;
    r = r_max / plot_num * i;
    x = r * cos(theta);
    y = r * sin(theta);

    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();
  
  // 中心をプロット
  plot_point(0.0,0.0);

}

// 極座標が(a,alpha)である点Ａを通り、ＯＡに垂直な直線を極方程式で描く
void draw_line_polor2(
  float a, // 動径
  float alpha // 始線とのなす角
){

  // グラフを描画
  int plot_num = 2000; // グラフを描くための頂点の最大個数
  
  float r, theta; // 極座標
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<=plot_num; i++){
    theta = alpha - PI + 2.0 * PI / plot_num * i;
    if( cos(theta - alpha)>0 ){
      r = a / cos(theta - alpha);
      x = r * cos(theta);
      y = r * sin(theta);

      // キャンバス上の座標位置に換算
      X = width / 2.0 / x_range * x;
      Y = height / 2.0 / y_range * y;
      vertex(X, Y);
    }
  }
  endShape();
  
  // 点Aをプロット
  x = a * cos(alpha);
  y = a * sin(alpha);
  plot_point(x,y);

}

// 座標(x,y)に点をプロットする関数
void plot_point(
  float x, // 点のx座標
  float y  // 点のy座標
){
  float X, Y; // キャンバス上の座標
  // キャンバス上の座標位置に換算
  X = width / 2.0 / x_range * x;
  Y = height / 2.0 / y_range * y;
  strokeWeight(5);
  point(X, Y);
  strokeWeight(1);
}

ソースコード2　極方程式を用いて直線を描くプログラム

ソースコード2では、直線の極方程式[1]を用いて直線を描く関数を　draw_line_polor1 とし、直線の極方程式[2]を用いて直線を描く関数を　draw_line_polor2 として準備して setup 関数内で利用するようにしています。
なお、draw_line_polor2 関数では、$${\theta}$$を$${\alpha - \pi}$$から$${\alpha + \pi}$$まで動かすようにしています。これは直線が無限大まで行ったあと、その反対の無限大へのトビが発生しないようにするためです。

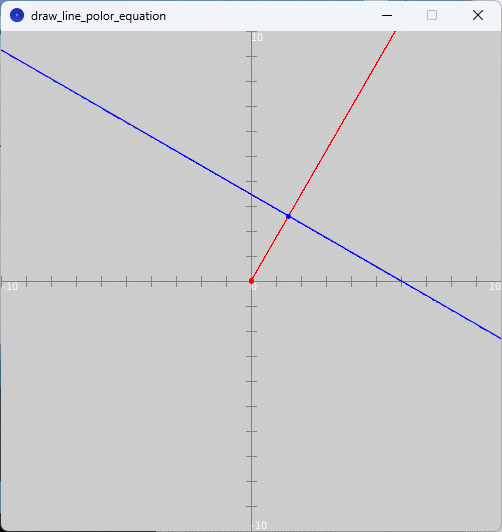
スケッチ「draw_line_polor_equation」の「draw_line_polor_equation」タブを選択してそのテキストエディタ部分をソースコード2で書き換えて実行すると、図2のように、実行ウィンドウのキャンバスの$${xy}$$平面上に、直線の極方程式[1]による直線が赤色、直線の極方程式[2]による直線が青色でそれぞれ描かれます。なお、始線とのなす角$${\alpha}$$はともに$${\alpha=\pi/3}$$とし、直線の極方程式[2]で利用する点$${\mathrm{A}}$$の動径$${a}$$は$${a=3}$$として描いています。

極方程式を用いた２次曲線の描画

最後に、極方程式を用いて２次曲線を描くプログラムを考えていきます。

アルゴリズム設計

２次曲線の極方程式の場合、動径$${r}$$が偏角$${\theta}$$に依存しますので、偏角$${\theta}$$を$${0}$$から$${2 \pi}$$まで動かしながら、

$$
r= \frac{ea}{1+e \cos \theta }
$$

で動径$${r}$$の大きさを決定したあと、極座標から直交座標に変換した上で、点$${(x,y)}$$を順に結んでいくことで、２次曲線を描くことができます。ただし、円の極方程式や直線の極方程式のときと同様、１点注意が必要です。動径$${r}$$は$${0}$$以上の値になりますので、$${ 1+e \cos \theta \leq 0}$$となるような$${\theta}$$の領域では２次曲線の極方程式を利用することができません。そのため、今回のプログラムでは、$${ 1+e \cos \theta > 0}$$となるような$${\theta}$$の領域でのみ点を描くようにします。

プログラム

極方程式を用いて直線を描くプログラムを作成するにあたり、上記で作成したスケッチ「draw_circle_polor_equation」を再利用します。
スケッチ「draw_circle_polor_equation」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「draw_quadratic_curve_polor_equation」と変更し、またスケッチ「draw_quadratic_curve_polor_equation」内の「draw_circle_polor_equation.pde」ファイルの名前を「draw_quadratic_curve_polor_equation.pde」に変更します。そして、pdeファイル「draw_quadratic_curve_polor_equation.pde」をダブルクリックしてスケッチ「draw_quadratic_curve_polor_equation」の開発環境ウィンドウを立ち上げます。そして、開発環境ウィンドウのタブ欄で「draw_quadratic_curve_polor_equation」タブを選択して、そのテキストエリアのソースコードを以下のソースコード3に書き換えます。

float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500);
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  
  noFill();
  stroke(0,0,0);

  float a = 5.0; // 点A(a,0)
  float e; // 離心率
  
  // 楕円
  stroke(255,0,0);
  e = 0.5;
  draw_quadratic_curve_polor(a,e);
  
  // 放物線
  stroke(0,255,0);
  e = 1.0;
  draw_quadratic_curve_polor(a,e);

  // 双曲線
  stroke(0,0,255);
  e = 2.0;
  draw_quadratic_curve_polor(a,e);

}

// 離心率eの２次曲線を極方程式で描く
void draw_quadratic_curve_polor(
  float a, // 点A(a,0)
  float e  // 離心率 
){

  // グラフを描画
  int plot_num = 2000; // グラフを描くための頂点の最大個数
  
  float r, theta; // 極座標
  float denominator; // 極方程式の分母
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<=plot_num; i++){
    theta = 2.0 * PI / plot_num * i;
    denominator = 1.0 + e * cos(theta);
    if( denominator > 0 ){
      r = e * a / denominator;
      x = r * cos(theta);
      y = r * sin(theta);

      // キャンバス上の座標位置に換算
      X = width / 2.0 / x_range * x;
      Y = height / 2.0 / y_range * y;
      vertex(X, Y);
    }
  }
  endShape();
  
  // 点Aをプロット
  plot_point(a,0.0);

}

// 座標(x,y)に点をプロットする関数
void plot_point(
  float x, // 点のx座標
  float y  // 点のy座標
){
  float X, Y; // キャンバス上の座標
  // キャンバス上の座標位置に換算
  X = width / 2.0 / x_range * x;
  Y = height / 2.0 / y_range * y;
  strokeWeight(5);
  point(X, Y);
  strokeWeight(1);
}

ソースコード3　極方程式を用いて２次曲線を描くプログラム

ソースコード3では、２次曲線の極方程式を用いて２次曲線を描く関数を　draw_quadratic_curve_polor として準備しました。また、 draw_quadratic_curve_polor 関数を setup 関数内で利用する際に、離心率$${e}$$を調整することで、楕円（$${e=0.5}$$）、放物線（$${e=1}$$）、双曲線（$${e=2}$$）を描くようにしています。

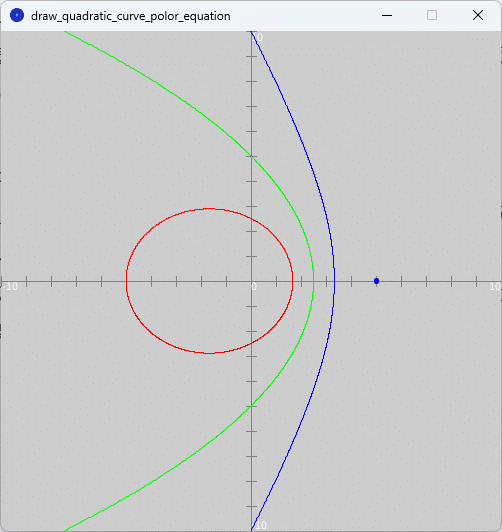
スケッチ「draw_quadratic_curve_polor_equation」の「draw_quadratic_curve_polor_equation」タブを選択してそのテキストエディタ部分をソースコード3で書き換えて実行すると、図3のように、実行ウィンドウのキャンバスの$${xy}$$平面上に、２次曲線の極方程式による楕円が赤色、放物線が緑色、双曲線が青色でそれぞれ描かれます。なお、点$${\mathrm{A}}$$の動径成分$${a}$$は$${a=5}$$としています。

まとめ

今回は、数学IIIで学ぶ「極方程式」について、極方程式を利用して円、直線、および２次曲線を描くプログラムを作成しました。
極方程式は一般に動径$${r}$$と偏角$${\theta}$$の関数となっていますが、動径方向が$${r \geq 0}$$の領域でのみ利用できることに注意が必要です。つまり、極方程式を単純に利用してしまうと、偏角$${\theta}$$の値によっては、$${r < 0}$$となってしまいます。そのため、今回作成したプログラムで$${r < 0}$$となってしまう偏角$${\theta}$$の領域では線を描かないようにしました。
また、直線の極方程式[1]を利用して描かれた直線は半直線となり（図2参照）、２次曲線の極方程式を利用して描かれた双曲線は２つの曲線のうち１つだけが描かれています。これらは極方程式を利用してグラフを描くときの特徴だと思います。足りない部分をどうしたら補えるか、これを考えることは勉強になると思いますので、是非考えてみてください。

読んだ感想などをお寄せください

本記事を読んだ感想や質問などを以下のお問い合せフォームからお寄せください。感想、質問をいただいた方には本記事の演習問題の解答をプレゼントします。（お問合せフォームの本文に、本記事のタイトルを入れてください。）

参考文献

改訂版教科書傍用スタンダード・オリジナル数学III（数研出版、ISBN9784410209567）

演習問題

次の曲線を極方程式で表したうえで、本記事で作成した関数を利用してそれらのグラフを描くプログラムを作成してください。

$$
(1) \ x=5 \\ (2) \ y=-\sqrt{3}x \\ (3) \ x+y-4=0 \\
(4) \ x^2+y^2=4x \\ (5) \ y^2=-4x+4 \\ (6) \ 3(x-4)^2-y^2=12
$$

演習問題の解答例

ここから先は

629字 / 1画像 / 1ファイル

ログイン

この記事が気に入ったらサポートをしてみませんか？