見出し画像

高校数学をプログラミングで解く（数学B編）「2-0-1 空間ベクトルを描く」

MK's papa

マガジンリスト　＞　数学B編 2.空間のベクトル　＞　2-0-1 空間ベクトルを描く


はじめに

今回はキャンバス上に設定された3次元座標系（右手系）を基準として空間ベクトルを描くための関数を作成し、その利用方法について説明していきます。
なお、空間ベクトルを描くための関数を作成するにあたり、そらたまごさんの『Processingで矢印を書く方法（3次元）』の記事を参考にさせてもらいました。

Processingで空間ベクトルを描く

記事『高校数学をプログラミングで解く（数学B編）「1-0 ベクトルを描く」』では、Processingで2次元べクトルを描く方法について解説しました。今回は、Processingでの空間ベクトル（３次元ベクトル）の描き方について解説していきます。
Processingでは、２次元のときと同様、空間ベクトルも PVector クラスを用いてほとんどのベクトル演算を行うことができますが、やはり、空間ベクトルを描くための関数などは用意されていません。そこで、この記事では、空間ベクトルを描くための関数を自作します。そして、今後の空間ベクトルの問題を考える際に利用していきます。

空間ベクトルのイメージ

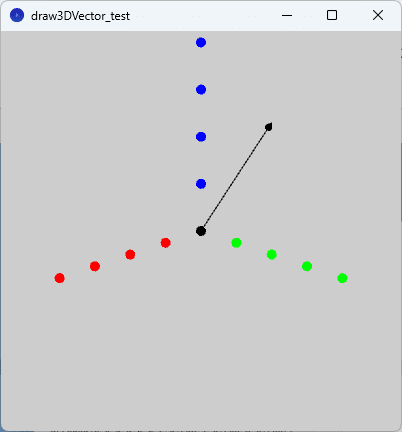
今回描く空間ベクトルのイメージを図1に示します。

図1　空間ベクトルのイメージ

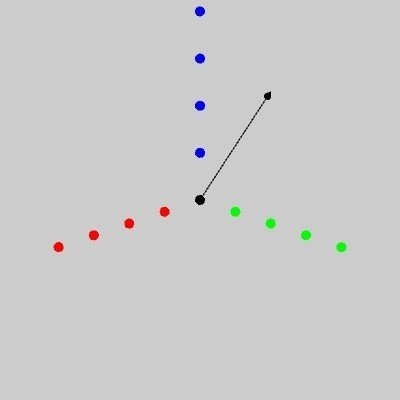
図1は、記事『高校数学をプログラミングで解く（準備編）「4-3 Processingでの3次元座標」』の『高校数学に適した3次元座標系を考える』の節で利用した「点列を描くプログラム（スケッチ「draw3DTest」）」に空間ベクトルを描いた例です。空間ベクトルを表す矢印の矢じりの部分を円錐で描いているのが特徴です。

空間ベクトルを描くための関数の準備

図1のような空間ベクトルを描くための関数 arrow3D を作成します。

// 空間ベクトルを描く関数
void arrow3D(
  float start_x, // ベクトルの始点のx座標
  float start_y, // ベクトルの始点のy座標
  float start_z, // ベクトルの始点のz座標
  float end_x, // ベクトルの終点のx座標
  float end_y, // ベクトルの終点のy座標
  float end_z  // ベクトルの終点のz座標
){
  // y軸方向の値の符号を変える（右手系→左手系）
  start_y *= -1.0;
  end_y *= -1.0;
  
  // 矢印の矢じり（円錐）を描くための準備
  int arrowLength = 10;
  float arrowAngle = 0.4;
  float phi = atan2(end_y-start_y, end_x-start_x);
  float theta = PI/2-atan2(end_z-start_z, 
    sqrt((end_x-start_x)*(end_x-start_x)+(end_y-start_y)*(end_y-start_y)));

  // 矢印のシャフト部分を描く
  line(start_x, start_y, start_z, end_x, end_y, end_z);

  // 矢印の矢じり（円錐）部分を描く
  strokeWeight(1); 
  pushMatrix();
  translate(end_x, end_y, end_z);
  rotateZ(phi);
  rotateY(theta);
  cone(arrowLength,arrowLength*sin(arrowAngle));
  popMatrix();

}

// 円錐を描く関数
void cone(
  int L, 
  float radius
){
  float x, y;
  int polygon_size = 100;
  noStroke();
  beginShape(TRIANGLE_FAN);  // 底面の円の作成
  vertex(0, 0, -L);
  for(int i=0; i<polygon_size; i++){
    x = radius*cos(radians(360.0/polygon_size*i));
    y = radius*sin(radians(360.0/polygon_size*i));
    vertex(x, y, -L);
  }
  endShape(CLOSE);
  beginShape(TRIANGLE_FAN);  // 側面の作成
  vertex(0, 0, 0);
  for(int i=0; i<polygon_size; i++){
    x = radius*cos(radians(360.0/polygon_size*i));
    y = radius*sin(radians(360.0/polygon_size*i));
    vertex(x, y, -L);
  }
  endShape(CLOSE);
}

ソースコード1　空間ベクトルを描くための関数

ソースコード1の arrow3D 関数の引数は以下の通りとなります。

start_x：ベクトルの始点の$${x}$$座標　float型
start_y：ベクトルの始点の$${y}$$座標　float型
start_z：ベクトルの始点の$${z}$$座標　float型
end_x：ベクトルの終点の$${x}$$座標　float型
end_y：ベクトルの終点の$${y}$$座標　float型
end_z：ベクトルの終点の$${z}$$座標　float型

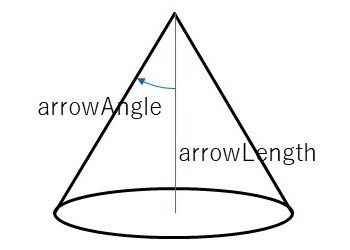
また、空間ベクトルの矢じり部分の円錐を描く関数 cone を用意しています。cone 関数の引数は以下の通りとなります（図2参照）。

L：円錐の高さ　float型
radius：円錐の底面となる円の半径　float型

図2　円錐の高さと底面の円の半径

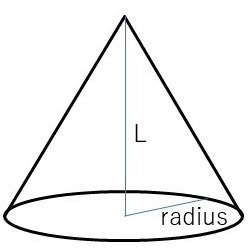
ただし、cone 関数は直接利用せず、arrow3D 関数から呼び出す形で利用するため、空間ベクトルを描く際に cone 関数の引数を意識する必要はありません。

空間ベクトルを描くための関数をpdeファイルに保存

今回作成した空間ベクトルを描くための関数 arrow3D（ソースコード1）は今後何度も再利用していくので、pdeファイル「setArrow3D.pde」として保存しておきます。これを、スケッチ「draw3DTest」に空間ベクトルを描く関数（ソースコード1）を「setArrow3D.pde」として追加する形で作成します。

① 記事『高校数学をプログラミングで解く（準備編）「4-3 Processingでの3次元座標」』で作成したスケッチ「draw3DTest」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「draw3DVector_test」と変更し、またスケッチ「draw3DVector_test」内の「draw3DTest.pde」ファイルの名前を「draw3DVector_test.pde」に変更します（図3）。

図3　スケッチ「draw3DVector_test」のフォルダ

② pdeファイル「draw3DVector_test.pde」をダブルクリックしてスケッチ「draw3DVector_test」の開発環境ウィンドウを立ち上げます（図4）。その結果、開発環境ウィンドウのタブ欄には「draw3DVector_test」タブが表示されます。

図4　スケッチ「draw3DVector_test」の開発環境ウィンドウ

③ スケッチ「draw3DVector_test」の開発環境ウィンドウのタブ欄にある▼のボタンを押して「新規タブ」を選択し、新たに「setArrow3D」タブを追加します（図5）。

図5　「setArrow3D」タブを追加

また、このとき、スケッチ「draw3DVector_test」のフォルダに、pdeファイル「setArrow3D.pde」が追加されます（図6）。

図6　「setArrow3D.pde」ファイルの追加

④ 「setArrow3D」タブを選択した状態で、そのテキストエリアに arrow3D 関数及び cone 関数（ソースコード1）を記述します（図7）。

図7　arrow3D 関数を記述

⑤ 「draw3DVector_test」タブを選択し、そのテキストエリアに arrow3D 関数を呼び出すコードを追記していきます（ソースコード2、図8）。

void setup(){
  size(400, 400, P3D); // 3次元空間を利用するためにP3Dを設定
  noLoop();
  // 視点を設定する
  camera(width/2.0, -height/2.0, height/4.0, 0.0, 0.0, 0.0, 0.0, 0.0, -1.0);
  // 平行投影法で描く
  ortho();
  // 座標系での表示範囲-range≦x,y.z≦range
  float range = 10.0;
  // 座標系のサイズをキャンバスのサイズに変換するパラメータ
  float res = width / 2.0 / range;

  // 点のサイズを設定
  strokeWeight(10);
  
  // 座標系の原点に点を打つ（黒色）
  point(0.0,0.0,0.0);
  
  // x軸上に点列を並べる（赤色）
  stroke(255,0,0);
  for(int i=1; i<=4; i++){
    point(50.0*i,0.0,0.0);
  } 
  
  // y軸上に点列を並べる（緑色）
  stroke(0,255,0);
  for(int i=1; i<=4; i++){
    point(0.0,-50.0*i,0.0);
  } 
  
  // z軸上に点列を並べる（青色）
  stroke(0,0,255);
  for(int i=1; i<=100; i++){
    point(0.0,0.0,50.0*i);
  }
  
  // 3Dベクトルを描く
  strokeWeight(1);
  fill(0,0,0);
  stroke(0,0,0);
  arrow3D(0.0,0.0,0.0,2.0*res,7.0*res,8.0*res);
}

ソースコード2　arrow3D 関数を呼び出して空間ベクトルを描くプログラム

図8　arrow3D 関数を呼び出すコードを記述

なお、ソースコード2では、arrow3D 関数を呼び出している部分

  // 3Dベクトルを描く
  strokeWeight(1);
  fill(0,0,0);
  stroke(0,0,0);
  arrow3D(0.0,0.0,0.0,2.0*res,7.0*res,8.0*res);

だけではなく、3次元座標系の表示範囲を表すパラメータ range と、座標系のサイズをキャンバスのサイズに変換するパラメータ res とを導入していることに注意してください。

  // 座標系での表示範囲-range≦x,y.z≦range
  float range = 10.0;
  // 座標系のサイズをキャンバスのサイズに変換するパラメータ
  float res = width / 2.0 / range;

⑥ 最後に、実行ボタンを押すと、実行ウィンドウのキャンバスに図1と同じ空間ベクトルを描いた画像が表示されます（図9）。

図9　空間ベクトルの描画

補足「座標軸とベクトルのスケールを合わせる処理」

上記の手順⑤で、arrow3D 関数を呼び出して空間ベクトルを描くプログラム（ソースコード2）に

  // 座標系での表示範囲-range≦x,y.z≦range
  float range = 10.0;
  // 座標系のサイズをキャンバスのサイズに変換するパラメータ
  float res = width / 2.0 / range;

を導入していることを説明しました。この部分は、3次元座標系の表示範囲を設定した上で、その座標系のサイズとキャンバスのサイズを合わせるためのパラメータを設定しています。
今回、$${x}$$軸、$${y}$$軸、$${z}$$軸方向がともに$${-10}$$から$${10}$$までの範囲の領域がキャンバスの幅や高さとほぼ一致するように設定しました（視点などの関係から少しずれるので、”ほぼ一致”と書いています）。点（start_x, start_y, start_z）から点（end_x, end_y, end_z）への空間ベクトルをキャンバス上に描く場合は、座標系のサイズでキャンバス上に描くのではなく、キャンバスのサイズに変換してから描く必要があります。その際、座標系のサイズをキャンバスのサイズに変換するパラメータ res を利用します。記事『高校数学をプログラミングで解く（数学I編）「1-0-1 グラフを描くための準備（その1）」』や『高校数学をプログラミングで解く（数学B編）「1-0 ベクトルを描く」』でも同様の解説を行っていますので、そちらも参考にしてください。

setArrow3D.pdeファイルの再利用

空間ベクトルを描くための関数 arrow3D をpdeファイル「setArrow3D.pde」に保存したので、今後ベクトルを描く際にはpdeファイル「setArrow3D.pde」を再利用していきます。再利用方法は、記事『高校数学をプログラミングで解く（準備編）「3-3 pdeファイルの再利用」』で説明していますので、そちらをご覧ください。

空間ベクトルを描く関数の解説

『高校数学をプログラミングで解く』の趣旨とは少しずれますが、空間ベクトルを描く関数について少し解説しておきます。

プログラムの解説１「右手系から左手系への変換」

まず、空間ベクトルを描く関数（ソースコード1）の

  // y軸方向の値の符号を変える（右手系→左手系）
  start_y *= -1.0;
  end_y *= -1.0;

の部分です。arrow3D関数の6つの引数は（start_x, start_y, start_z）の組で空間ベクトルの始点の座標を、（end_x, end_y, end_z）の組で空間ベクトルの終点の座標を表していますが、どちらも高校数学で利用される右手座標系で表されています。一方、Processingで用意されている関数などはすべて左手座標系を基準に準備されています。そのため、この部分で$${y}$$軸方向の値の符号を変えることで右手系の座標を左手系の座標に変換してから図形を描くための関数に利用しています。

プログラムの解説2「矢じりを描くためのパラメータ」

次に、空間ベクトルを描く関数（ソースコード1）の

  // 矢印の矢じり（円錐）を描くための準備
  int arrowLength = 10;
  float arrowAngle = 0.4;
  float phi = atan2(end_y-start_y, end_x-start_x);
  float theta = PI/2-atan2(end_z-start_z, 
    sqrt((end_x-start_x)*(end_x-start_x)+(end_y-start_y)*(end_y-start_y)));

の部分です。この部分は、空間ベクトルを表す矢印の矢じり部分を描くための各種パラメータを設定しています。
arrowLength：矢じり部分の高さ　float型
arrowAngle：矢じり部分の角度（ラジアン）　float型

図10　矢じり部分のパラメータ設定

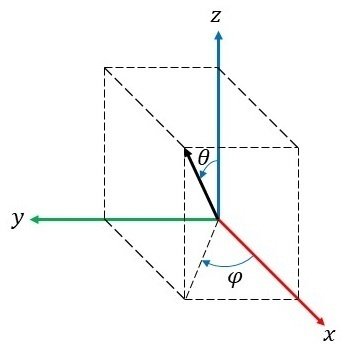
theta：$${z}$$軸正の向きと空間ベクトルとの間の角度$${\theta}$$　float型
phi：空間ベクトルを$${xy}$$平面に射影したベクトルと$${x}$$軸正の向きとの間の角度$${\varphi}$$　float型

図11　空間ベクトルの向きの極座標表示（左手系）

なお、パラメータ theta と phi は、矢じりの向きを空間ベクトルの向きに合わせるために利用します。

プログラムの解説3「円錐を描く関数 cone」

cone 関数は円錐を描くための関数です。Processingには、円錐を描くための関数は用意されていないので、自作しています。
まず、円錐は、その頂点が3次元座標系の原点と一致し、また円錐の中心軸が$${z}$$軸方向と一致するように設定します。
そして、今回円錐は細長い二等辺三角形を円錐の傘に貼り付けていって作成します（図12）。

図12　円錐の作成イメージ

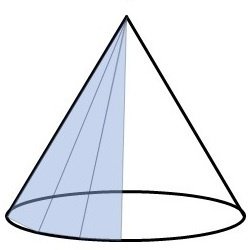
この傘部分への二等辺三角形の貼り付けは、記事『高校数学をプログラミングで解く（準備編）「2-3 Processingで多角形を描く」』で紹介した beginShape 関数と endShape 関数を利用しますが、beginShape 関数の引数に”TRIANGLE_FAN”という文字列を設定します。
この”TRIANGLE_FAN”を設定すると、どのような図形が描かれるのかを試してみます。

void setup(){
  size(400, 400);
  noLoop();
  translate(width/2, height/2);

  beginShape(TRIANGLE_FAN);
  vertex(0.0,0.0);
  vertex(150.0, 0.0);
  vertex(0.0, 150.0);
  vertex(-150.0, 0.0);
  vertex(0.0, -150.0);
  endShape(CLOSE);  
}

ソースコード3　TRIANGLE_FANを利用したテストプログラム

このソースコード3を、Processingの開発環境ウィンドウを開いて（スケッチ名を「TRIANGLE_FAN_test」としています）、テキストエディタ部分に書いて実行すると、図13のように実行ウィンドウのキャンバス上に3つの直角二等辺三角形を並べた図形が描かれます。

図13　スケッチ「TRIANGLE_FAN_test」の実行結果

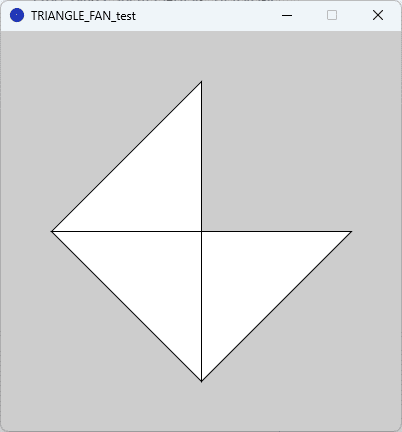
ソースコード3の beginShape 関数と endShape 関数との間には、５つの vertex 関数が並んでいます。これらの vertex 関数と図13を見比べると、最初の頂点と2番目、3番目の頂点から右下の直角二等辺三角形が得られ、次に、最初の頂点と3番目、4番目の頂点から左下の直角二等辺三角形が得られ、最後に、最初の頂点と4番目、5番目の頂点から左上の直角二等辺三角形が得られていることがわかります。
つまり、beginShape 関数の引数に”TRIANGLE_FAN”を設定すると、最初に与えた頂点と、2番目以降の頂点を順に2個ずつ取ってきてそれら3つを頂点とする三角形を作成して、順に描いていくということがわかります。

これは3次元空間でも利用することができるので、細長い二等辺三角形を円錐の傘に貼り付けるようなことができます。つまり、円錐の頂点をvertex関数を用いて最初の頂点とし、底面の円の円周を等分（今回は100等分）する点群を2番目以降の頂点として与えることで円錐を近似的に与えることができます。
また、底面の円についても今回は円の中心を最初の頂点とし、底面の円の円周を等分（今回は100等分）する点群を2番目以降の頂点として与えることで正多角形で近似して描いています。

プログラムの解説4「矢じり部分の角度を調整する」

最後に、空間ベクトルを描く関数（ソースコード1）の

  // 矢印の矢じり（円錐）部分を描く
  strokeWeight(1); 
  pushMatrix();
  translate(end_x, end_y, end_z);
  rotateZ(phi);
  rotateY(theta);
  cone(arrowLength,arrowLength*sin(arrowAngle));
  popMatrix();

の部分です。この部分は、空間ベクトルの矢印の矢じりの部分を描くためのコードです。
pushMatrix 関数と popMatrix 関数とについては記事『高校数学をプログラミングで解く（数学B編）「1-0 ベクトルを描く」』で詳しく解説していますので、そちらをご覧いただくとして、残りの部分について解説します。
まず、

translate(end_x, end_y, end_z);

により、円錐を描く3次元座標系の原点を空間ベクトルの終点の位置に合わせます。次に、

rotateZ(phi);

により、円錐を描く3次元座標系を$${z}$$軸周りに phi だけ回転させます（図14）。

図14　3次元座標系をz軸周りで回転

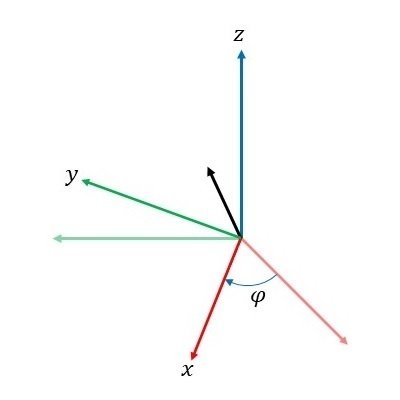
さらに、

 rotateY(theta);

により、$${z}$$軸周りに phi だけ回転した後の円錐を描く3次元座標系に対して$${y}$$軸周りに theta だけ回転させます（図15）。

図15　3次元座標系をy軸周りで回転

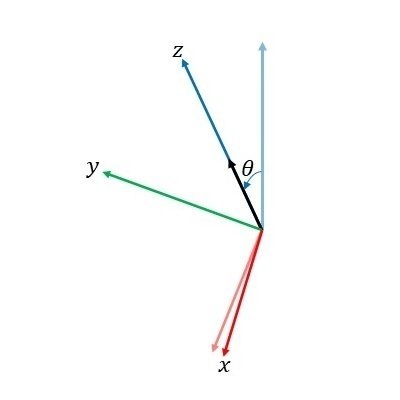
最後に、この移動、回転した3次元座標系の上に cone 関数を用いて円錐を描き、矢じり部分とします（図16）。

図16　移動回転した3次元座標系上で円錐を描く

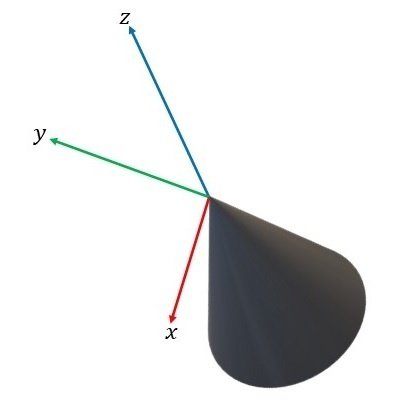
まとめ

今回はキャンバス上に設定された3次元座標系（右手系）を基準として空間ベクトルを描くための関数を作成し、その利用方法について説明しました。
なお、今回作成したベクトルを描くための関数 arrow3D についてその解説も行いましたが、『高校数学をプログラミングで解く』でお伝えしたい範囲を超える部分もあります。そのため、最初は関数の詳細にはこだわらず、関数の利用方法だけ知っておいてもらえれば、今後ベクトルを描く際に支障はありませんので、そのまま先の記事に進んでください。

参考文献

Webサイト『Processingで矢印を書く方法（3次元）』

改訂版 教科書傍用 スタンダード 数学B（数研出版、ISBN9784410209468）

Processingをはじめよう 第２版（オライリー・ジャパン、オーム社、ISBN9784873117737）


いいなと思ったら応援しよう！