書籍「教養としての「数学Ⅰ・A」」を読む（その９）

2024年12月15日 10:00

マガジンリスト　＞　書籍「教養としての「数学Ⅰ・A」」を読む　＞　その９

整数はアルゴリズムの土台になっている

上記の「教養としての「数学I・A」」を読み進めています。
今回は、最後の章「第８章　千年の謎をまとう数　整数の性質」を読みました。

ショッピングサイトにせよ暗号資産にせよ、現代のネット関連技術は、素数を利用した暗号の上に成立しているといっても過言ではありません。また、コンピュータを効果的に使いこなすためには、2 進数・16 進数やアルゴリズムに関する知識が必要になってきますが、それらの土台となる内容も含まれています。

p.248

『コンピュータを効果的に使いこなすためには、アルゴリズムに関する知識が必要になってきます』というところに目が留まりました。
確かに、現在のコンピュータ内で行う演算処理は全て 2 進数で行いますので、アルゴリズムの土台は整数の性質をきちんと理解することにつながりますね。整数の性質を学ぶ意義をあらためて感じました。

約数を探すためには

これは$${N}$$の約数（割り切れる数）を探すときには
$${a \times a \leq a \times b = N \Rightarrow a^2 \leq N \Rightarrow a \leq \sqrt{N}}$$
の範囲の$${a}$$で$${N}$$を割ってみれば良いことを意味します。

p.251

これは勉強になりました。
この note の記事『高校数学をプログラミングで解く（数学A編）「3-1 約数と倍数」』で以下のような整数$${N}$$以下の素数を求めるプログラム（ソースコード1）を作成しましたが、もう少し改良ができそうです。

// 整数N以下の素数を求める
void setup(){
  // 整数N（ただし、Nは2以上）
  int N;
  N = 20;

  println(2); // 最初の素数をコンソールに出力
  
  boolean pn_flag; // 素数かどうかのフラグ
  // 3以上N以下の整数について素数であるかを確認する
  for(int n=3; n<=N; n+=2){
    pn_flag = true;
    for(int m=3; m<n; m+=2){
      if( n%m == 0 ){ // mで割り切れたらnは素数でない
        pn_flag = false;
        break;
      }
    }
    if(pn_flag){ // nが素数と判定されたらコンソールに出力
      println(n);
    }
  }
}

ソースコード1　整数$${N}$$以下の素数を求めるプログラム

つまり、このソースコード1の

    for(int m=3; m<n; m+=2){

の部分は、上記の条件から

    for(int m=3; m<=sqrt(n); m+=2){

と改良することができるわけです。改良した結果、整数$${N}$$以下の素数を求めるプログラムを実行してみると、図1のように、コンソールに

2
3
5
7
11
13
17
19

と出力されます。

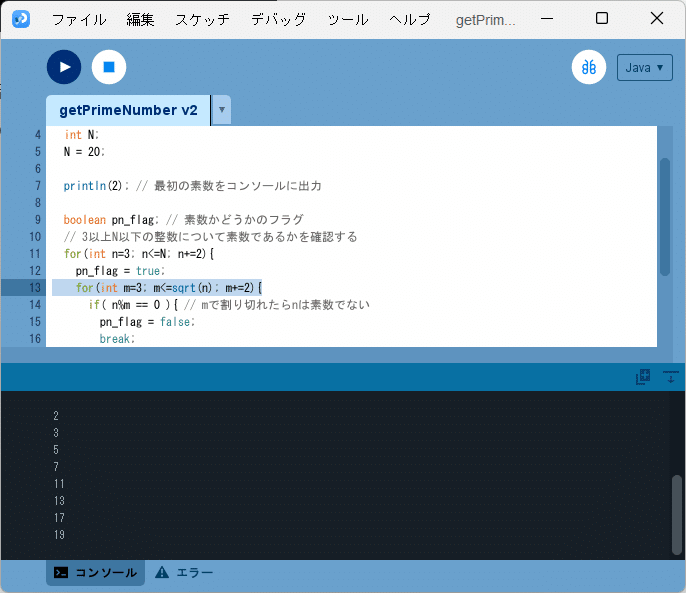
この例では、$${N=20}$$ですので、あまり大きな効果は期待できませんが、$${N}$$をもっと大きな整数にしたときは、その処理時間に今回の改良の効果が見えてくるのではないかと思います。

整数問題のアプローチ

① 積の形をつくる
② 「互いに素」の利用
③ ある整数で割った余りで分類
④ 必要条件による絞り込み
⑤ 極端な例を考える

p.263

これら5つの整数問題へのアプローチ方法をみていて、ふとプログラムのテスト技法を思い出しました。アルゴリズム設計知識を身につけることと整数の性質を理解することとはやはり切っても切り離せないことなのかもしれません。

素数と n 進法

たとえば、$${10}$$進法の$${6}$$は$${2 \times 3}$$で表せますから、もちろん素数ではありません。$${10}$$進法の$${6}$$は、$${2}$$進法で表せば$${110}$$。これは$${10}$$（$${10}$$進法の$${2}$$）と$${11}$$（$${10}$$進法の$${3}$$）の積で表せますからやはり素数ではありません。これは、$${2}$$進法に限らず、何進法で考えても同じです。

p.276-277

$${n}$$進法での素数については以前から何となく気になっていたので、今回大変勉強になりました。
あと、こちらもなんとなくですが、整数が素数であるかどうかを考える際に、$${10}$$進法で考えるより、$${2}$$進法で考える方がやりやすいのではないかと思いました。

今回の話（第８章）は、「数学A」で学ぶ「整数の性質」のお話でした。整数の性質については、コンピュータ（アルゴリズム設計、プログラミングなど）と切っても切り離せないことだとあらためて実感しました。
なお、大学入試共通テストでは、数学Ⅰ・A の単元で「整数の性質」について扱わないそうです。「整数の性質」の内容がなくなったのではなく、「情報Ⅰ」で扱うようにするということではないかと推測します。
この note にまとめている記事（マガジン）『高校数学をプログラミングで解く（数学A編）3.整数の性質』では、この章で扱っている内容を実際にプログラミングしているものもあるので、合わせて読んでいただければと思います。

今回でこの書籍の紹介は終わりです。読んでいただいてありがとうございました。

MK's papa