数学花壇　〜放物線編⑨〜

エピソード9：イメージだけに頼るな！だが頼れ！

すでにこのこと自体が幻術なんじゃないか？
名前を確かめてみなさいってことですね？任せてください。

こんな感じで名前を確かめてみました。

「よき。確かにParabola y²=4xになったのう。確認じゃが定直線の位置はどこでもよかったかのう？」

いいえ、原点と準線の間です。

「原点と準線の間ならどこでもよかったかのう？」

はい、そのはずです。

「では定直線はx=a（-1<a<0）としたら定円の半径はどうなるかのう？」

ええっと、定直線と準線との距離が定円の半径になればいいから・・・
a+1でしょうか？

「うむ。その設定で名前を確かめてみよ。」

確かめるといっても定直線をx=-1/2からx=aに変えて、定円の半径を1/2からa+1に変えればいいだけですよね？

「そうだのう。」

こんな感じでしょうか？

「よき。三平方の定理を使わずに示せるかのう？」

別の方法で確かめるってことですか？

「うむ。Parabolaは正方形と長方形の面積の一致だったが、放物線の定義はなんだったかのう？」

定義？そんな話はなかったと思いますが？

「そうだったかえ？Parabolaをとらえるために最初にした質問は何だったかのう？」

点Fと、点Fを通らない直線Lから等しい距離にある点Pはいくつある・・・
もしかして教科書通りの定義を使っていいんですか？

「うむ。いつ使ってはいけないと言ったかえ？」

わかりました、定義を使って示してみます。

そうか！PHの長さが、PAの長さと等しいことを示せばいいのか！

こんな示し方でどうでしょうか？

「よきよき。もう一度聞くが、定直線の位置はどこでもよかったかのう？」

さっき答えたばかりなのになぜ？
いいえ、準線と原点の間です。

「本当にそうかのう？」

ちゃんとParabolaになることを示せたから問題はないはずです。

「示せたのは定直線が準線と原点間にある範囲内であって、その範囲外では成り立たないことを示せたわけではないのう。」

確かにそうですが、これ以外のイメージが・・・

「定直線が準線を越えるとどうなるかえ？」

動く円の半径が、点Pと定円の中心との距離を越えてしまいます。

「そうなるとどうなるかのう？」

動く円が定円と2点で交わります。

「そうだのう。それで？」

もっと大きくすると交わらなくなってしまいます。

「そうだのう。それで？」

それ以上はずっと交わりません。

「そうだのう。それで？」

・・・もうこれ以上は答えることはないです。

「2点で交わると、交わらなくなるの間は何かえ？」

2点で交わると、交わらなくなるの間？あっ、そうか、1点で交わる瞬間！
すいません、見落としていました。1点で接します。

「そうだのう。イメージを共有するかのう。」

定直線と定円に内接する円の中心の軌跡

わっ、すごい！内接していてもParabolaがつくれている！接するというと、外接するイメージばかりを思い浮かべていたけど、内接する場合もあったんだ！
ありがとうございます、内接までイメージできてなかったです。

「よき。これは定直線がx=-2で、定円は中心が(1, 0)で半径が1じゃ。」

名前を確かめるかのうですね？

「うむ。」

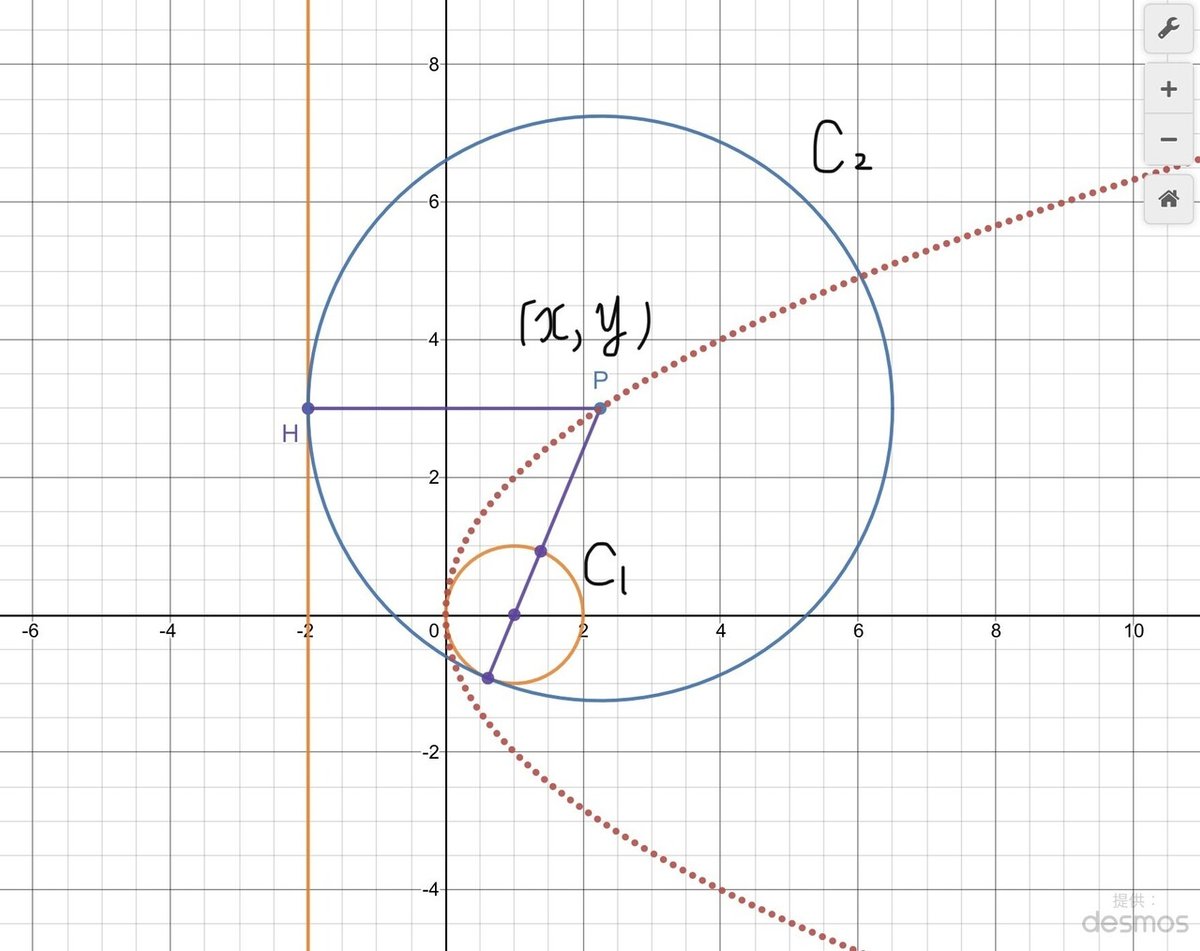
求まりました！Parabola y²=4xになる設定だったんですね！

「うむ。外接、内接どっちでもつくれることを体感できたじゃろう。」

はい。

「じゃがまだ体感は終わってない。定直線は準線を越えているならどこでもよかったかのう？」

・・・外接のときと同じように定直線をx=-2からx=aに変えて、定円の半径を1から-1-aに変えれば確かめられると思います。

「うむ。ならば」

その設定で名前を確かめてみよ。ですね。

エピソード10に続く。