More is different

ちまたではChatGPTをはじめとする大規模言語モデルの話題で持ちきりです。ChatGPTを使っていると、約3ヶ月前の2023年3月14日に爆誕したGPT-4が人間とみまちがうような回答を返してくれるのはなぜか？そもそもいままでの人工知能とどう違い、人間はGPT-4になぜこれほどはまってしまうのか？という疑問が生まれます。私のこの疑問に対してもっともわかりやすく説明してくれたのがアハ体験で有名になった茂木先生の動画です。

この中で、人工知能を人工知能にたらしめるには「人間と会話してその回答が人間と分別つかないことである」という人工知能を見分ける有名なチェック方法であるチューリングテストに言及し、さらにそれをより具体的にした「ウィノグラード・スキーマ・チャレンジ」や「心の理論」、「誤信念課題」について紹介してくれています。

これらは主に子供の発達にかかわる認知心理学の話なのですが、その解説は別の機会に設けるとして、上述の茂木さんの動画で紹介されている最も印象的な話に物性物理学権威でノーベル賞物理学者のフィリップ・アンダーソンの論文「More is different」が紹介されています。本論文は、フィリップ・アンダーソンがいきすぎた還元主義を本質的に批判するために1972年8月に科学論文雑誌Scienceに執筆ものです。とても有益な論文なのですが、原文は画像としてのPDFはネットに落ちているものの、テキストや全文訳が見当たらなかったので、少し長文ですがすぐにコピペして使えるように全文をテキスト化してみました。

More Is Different
Broken symmetry and the nature of the hierarchical structure of science.
P. W. Anderson

The reductionist hypothesis may still be a topic for controversy among phi­losophers, but among the great majority of active scientists I think it is accepted without question. The workings of our minds and bodies, and of all the ani­mate or inanimate matter of which we have any detailed knowledge, are as­sumed to be controlled by the same set of fundamental laws, which except under certain extreme conditions we feel we know pretty well.

It seems inevitable to go on uncrit­ically to what appears at first sight to be an obvious corollary of reductionism: that if everything obeys the same fundamental laws, then the only sci­entists who are studying anything really fundamental are those who are working on those laws. In practice, that amounts to some astrophysicists, some elemen­tary particle physicists, some logicians and other mathematicians, and few others. This point of view, which it is the main purpose of this article to oppose, is expressed in a rather well- known passage by Weisskopf (1):

Looking at the development of science in the Twentieth Century one can dis­tinguish two trends, which I will call “intensive” and “extensive” research, lack­ing a better terminology. In short: in­tensive research goes for the fundamental laws, extensive research goes for the explanation of phenomena in terms of known fundamental laws. As always, dis­tinctions of this kind are not unambiguous, but they are clear in most cases. Solid state physics, plasma physics, and perhaps also biology are extensive. High energy physics and a good part of nuclear physics are intensive. There is always much less intensive research going on than extensive. Once new fundamental laws are discov­ered, a large and ever increasing activity begins in order to apply the discoveries to hitherto unexplained phenomena. Thus, there are two dimensions to basic re­search. The frontier of science extends all along a long line from the newest and most modern intensive research, over the ex­tensive research recently spawned by the intensive research of yesterday, to the broad and well developed web of exten­sive research activities based on intensive research of past decades.

The effectiveness of this message may be indicated by the fact that I heard it quoted recently by a leader in the field of materials science, who urged the participants at a meeting dedicated to “fundamental problems in condensed matter physics” to accept that there were few or no such problems and that nothing was left but extensive science, which he seemed to equate with device engineering.

The main fallacy in this kind of thinking is that the reductionist hypoth­esis does not by any means imply a “constructionist” one: The ability to reduce everything to simple fundamen­tal laws does not imply the ability to start from those laws and reconstruct the universe. In fact, the more the ele­mentary particle physicists tell us about the nature of the fundamental laws, the less relevance they seem to have to the very real problems of the rest of sci­ence, much less to those of society.

The constructionist hypothesis breaks down when confronted with the twin difficulties of scale and complexity. The behavior of large and complex aggre­gates of elementary particles, it turns out, is not to be understood in terms of a simple extrapolation of the prop­erties of a few particles. Instead, at each level of complexity entirely new properties appear, and the understand­ing of the new behaviors requires re­search which I think is as fundamental in its nature as any other. That is, it seems to me that one may array the sciences roughly linearly in a hierarchy, according to the idea: The elementary entities of science X obey the laws of science Y.

X:
- solid state or many-body physics chemistry
- molecular biology cell biology
...
- psychology
- social sciences

Y:
- elementary particle physics
- many-body physics chemistry
- molecular biology
...
- physiology
- psychology

But this hierarchy does not imply that science X is “just applied Y." At each stage entirely new laws, concepts, and generalizations are necessary, re­quiring inspiration and creativity to just as great a degree as in the previous one. Psychology is not applied biology, nor is biology applied chemistry.

In my own field of many-body phys­ics, we are, perhaps, closer to our fun­damental, intensive underpinnings than in any other science in which non­trivial complexities occur, and as a re­sult we have begun to formulate a general theory of just how this shift from quantitative to qualitative differ­entiation takes place. This formulation, called the theory of "broken sym­metry," may be of help in making more generally clear the breakdown of the constructionist converse of reductionism. I will give an elementary and in­complete explanation of these ideas, and then go on to some more general spec­ulative comments about analogies at other levels and about similar phe­nomena.

Before beginning this I wish to sort out two possible sources of misunder­standing. First, when I speak of scale change causing fundamental change I do not mean the rather well-understood idea that phenomena at a new scale may obey actually different fundamen­tal laws—as, for example, general rela­tivity is required on the cosmological scale and quantum mechanics on the atomic. I think it will be accepted that all ordinary matter obeys simple elec­trodynamics and quantum theory, and that really covers most of what I shall discuss. (As I said, we must all start with reductionism, which I fully ac­cept.) A second source of confusion may be the fact that the concept of broken symmetry has been borrowed by the elementary particle physicists, but their use of the term is strictly an analogy, whether a deep or a specious one remaining to be understood.

Let me then start my discussion with an example on the simplest possible level, a natural one for me because I worked with it when I was a graduate student: the ammonia molecule. At that time everyone knew about ammonia and used it to calibrate his theory or his apparatus, and I was no exception.

Triangular pyramid of ammonia

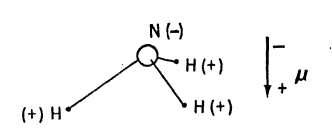
The chemists will tell you that ammonia “is” a triangular pyramid with the nitrogen negatively charged and the hydrogens positively charged, so that it has an electric dipole mo­ment (μ), negative toward the apex of the pyramid. Now this seemed very strange to me, because I was just being taught that nothing has an electric di­pole moment. The professor was really proving that no nucleus has a dipole moment, because he was teaching nu­clear physics, but as his arguments were based on the symmetry of space and time they should have been correct in general.

I soon learned that, in fact, they were correct (or perhaps it would be more accurate to say not incorrect) because he had been careful to say that no stationary state of a system (that is, one which does not change in time) has an electric dipole moment. If am­monia starts out from the above unsymmetrical state, it will not stay in it very long. By means of quantum me­chanical tunneling, the nitrogen can leak through the triangle of hydrogens to the other side, turning the pyramid inside out, and, in fact, it can do so very rapidly. This is the so-called “in­version,” which occurs at a frequency of about 3 x 10^10 per second. A truly stationary state can only be an equal superposition of the unsymmetrical pyramid and its inverse. That mix­ture does not have a dipole moment. (I warn the reader again that I am greatly oversimplifying and refer him to the textbooks for details.)

I will not go through the proof, but the result is that the state of the system, if it is to be stationary, must always have the same symmetry as the laws of motion which govern it. A reason may be put very simply: In quantum me­chanics there is always a way, unless symmetry forbids, to get from one state to another. Thus, if we start from any one unsymmetrical state, the system will make transitions to others, so only by adding up all the possible unsymmet­rical states in a symmetrical way can we get a stationary state. The symmetry involved in the case of ammonia is parity, the equivalence of left- and right-handed ways of looking at things. (The elementary particle experimental­ists' discovery of certain violations of parity is not relevant to this question; those effects are too weak to affect ordinary matter.)

Having seen how the ammonia mol­ecule satisfies our theorem that there is no dipole moment, we may look into other cases and, in particular, study progressively bigger systems to see whether the state and the symmetry are always related. There are other similar pyramidal molecules, made of heavier atoms. Hydrogen phosphide, PH3, which is twice as heavy as ammonia, inverts, but at one-tenth the ammonia frequency. Phosphorus trifluoride, PF3, in which the much heavier fluorine is substituted for hydrogen, is not observed to invert at a measurable rate, although theo­retically one can be sure that a state prepared in one orientation would in­ vert in a reasonable time.

We may then go on to more compli­cated molecules, such as sugar, with about 40 atoms. For these it no longer makes any sense to expect the molecule to invert itself. Every sugar molecule made by a living organism is spiral in the same sense, and they never invert, either by quantum mechanical tunnel­ing or even under thermal agitation at normal temperatures. At this point we must forget about the possibility of in­version and ignore the parity symmetry: the symmetry laws have been, not re­ pealed, but broken.

If, on the other hand, we synthesize our sugar molecules by a chemical re­action more or less in thermal equi­librium, we will find that there are not, on the average, more left- than right- handed ones or vice versa. In the ab­sence of anything more complicated than a collection of free molecules, the symmetry laws are never broken, on the average. We needed living matter to produce an actual unsymmetry in the populations.

In really large, but still inanimate, aggregates of atoms, quite a different kind of broken symmetry can occur, again leading to a net dipole moment or to a net optical rotating power, or both. Many crystals have a net dipole moment in each elementary unit cell (pyroelectricity), and in some this mo­ment can be reversed by an electric field (ferroelectricity). This asymmetry is a spontaneous effect of the crystal's seeking its lowest energy state. Of course, the state with the opposite mo­ment also exists and has, by symmetry, just the same energy, but the system is so large that no thermal or quantum mechanical force can cause a conversion of one to the other in a finite time com­pared to, say, the age of the universe.

There are at least three inferences to be drawn from this. One is that sym­metry is of great importance in physics. By symmetry we mean the existence of different viewpoints from which the sys­tem appears the same. It is only slightly overstating the case to say that physics is the study of symmetry. The first demonstration of the power of this idea may have been by Newton, who may have asked himself the question: What if the matter here in my hand obeys the same laws as that up in the sky - that is, what if space and matter are homogeneous and isotropic?

The second inference is that the in­ternal structure of a piece of matter need not be symmetrical even if the total state of it is. I would challenge you to start from the fundamental laws of quantum mechanics and predict the am­monia inversion and its easily observ­able properties without going through the stage of using the unsymmetrical pyramidal structure, even though no “state" ever has that structure. It is fascinating that it was not until a cou­ple of decades ago (2) that nuclear phys­icists stopped thinking of the nucleus as a featureless, symmetrical little ball and realized that while it really never has a dipole moment, it can become football­-shaped or plate-shaped. This has ob­servable consequences in the reactions and excitation spectra that are studied in nuclear physics, even though it is much more difficult to demonstrate di­rectly than the ammonia inversion. In my opinion, whether or not one calls this intensive research, it is as funda­mental in nature as many things one might so label. But it needed no new knowledge of fundamental laws and would have been extremely difficult to derive synthetically from those laws; it was simply an inspiration, based, to be sure, on everyday intuition, which sud­denly fitted everything together.

The basic reason why this result would have been difficult to derive is an important one for our further think­ing. If the nucleus is sufficiently small there is no real way to define its shape rigorously: Three or four or ten par­ticles whirling about each other do not define a rotating “plate” or “football.”
It is only as the nucleus is considered to be a many-body system - in what is often called the N → ♾️ limit - that such behavior is rigorously definable. We say to ourselves: A macroscopic body of that shape would have such-and-such a spectrum of rotational and vibrational excitations, completely different in na­ture from those which would character­ize a featureless system. When we see such a spectrum, even not so separated, and somewhat imperfect, we recognize that the nucleus is, after all, not macro­scopic; it is merely approaching macro­scopic behavior. Starting with the fun­damental laws and a computer, we would have to do two impossible things - solve a problem with infinitely many bodies, and then apply the result to a finite system - before we synthesized this behavior.

A third insight is that the state of a really big system does not at all have to have the symmetry of the laws which govern it; in fact, it usually has less symmetry. The outstanding example of this is the crystal: Built from a substrate of atoms and space according to laws which express the perfect homogeneity of space, the crystal suddenly and un- predictably displays an entirely new and very beautiful symmetry. The general rule, however, even in the case of the crystal, is that the large system is less symmetrical than the underlying struc­ture would suggest: Symmetrical as it is, a crystal is less symmetrical than perfect homogeneity.

Perhaps in the case of crystals this appears to be merely an exercise in confusion. The regularity of crystals could be deduced semi-empirically in the mid-19th century without any complicated reasoning at all. But some­ times, as in the case of superconduc­tivity, the new symmetry - now called broken symmetry because the original symmetry is no longer evident - may be of an entirely unexpected kind and ex­tremely difficult to visualize. In the case of superconductivity, 30 years elapsed between the time when physicists were in possession of every fundamental law necessary for explaining it and the time when it was actually done.

The phenomenon of superconductiv­ity is the most spectacular example of the broken symmetries which ordinary macroscopic bodies undergo, but it is of course not the only one. Anti-ferromagnets, ferroelectrics, liquid crystals, and matter in many other states obey a certain rather general scheme of rules and ideas, which some many-body the­orists refer to under the general heading of broken symmetry. I shall not further discuss the history, but give a bibliog­raphy at the end of this article (3).

The essential idea is that in the so-called N → ♾️ limit of large systems (on our own, macroscopic scale) it is not only convenient but essential to realize
that matter will undergo mathematically sharp, singular “phase transitions” to states in which the microscopic sym­metries, and even the microscopic equa­tions of motion, are in a sense violated. The symmetry leaves behind as its ex­pression only certain characteristic be­haviors, for instance, long-wavelength vibrations, of which the familiar exam­ple is sound waves; or the unusual mac­roscopic conduction phenomena of the superconductor; or, in a very deep analogy, the very rigidity of crystal lat­tices, and thus of most solid matter. There is, of course, no question of the system's really violating, as opposed to breaking, the symmetry of space and time, but because its parts find it ener­getically more favorable to maintain cer­tain fixed relationships with each other, the symmetry allows only the body as a whole to respond to external forces.

This leads to a “rigidity," which is also an apt description of superconduc­tivity and superfluidity in spite of their apparent "fluid" behavior. [In the for­mer case, London noted this aspect very early (4).] Actually, for a hypo­thetical gaseous but intelligent citizen of Jupiter or of a hydrogen cloud some­where in the galactic center, the proper­ ties of ordinary crystals might well be a more baffling and intriguing puzzle than those of superfluid helium.

I do not mean to give the impression that all is settled. For instance, I think there are still fascinating questions of principle about glasses and other amor­phous phases, which may reveal even more complex types of behavior. Never­theless, the role of this type of broken symmetry in the properties of inert but macroscopic material bodies is now un­derstood, at least in principle. In this case we can see how the whole becomes not only more than but very different from the sum of its parts.

The next order of business logically is to ask whether an even more com­plete destruction of the fundamental symmetries of space and time is possi­ble and whether new phenomena then arise, intrinsically different from the “simple” phase transition representing a condensation into a less symmetric state.

We have already excluded the appar­ently unsymmetric cases of liquids, gases, and glasses. (In any real sense they are more symmetric.) It seems to me that the next stage is to consider the system which is regular but contains information. That is, it is regular in space in some sense so that it can be “read out," but it contains elements which can be varied from one “cell" to the next. An obvious example is DNA; in everyday life, a line of type or a movie film have the same struc­ture. This type of “information-bearing crystallinity" seems to be essential to life. Whether the development of life requires any further breaking of sym­metry is by no means clear.

Keeping on with the attempt to char­acterize types of broken symmetry which occur in living things, I find that at least one further phenomenon seems to be identifiable and either universal or remarkably common, namely, ordering (regularity or periodicity) in the time dimension. A number of theories of life processes have appeared in which reg­ular pulsing in time plays an important role: theories of development, of growth and growth limitation, and of the mem­ory. Temporal regularity is very com­monly observed in living objects. It plays at least two kinds of roles. First, most methods of extracting energy from the environment in order to set up a continuing, quasi-stable process involve time-periodic machines, such as oscil­lators and generators, and the processes of life work in the same way. Second, temporal regularity is a means of han­dling information, similar to informa­tion-bearing spatial regularity. Human spoken language is an example, and it
is noteworthy that all computing ma­ chines use temporal pulsing. A possible third role is suggested in some of the theories mentioned above: the use of phase relationships of temporal pulses to handle information and control the growth and development of cells and organisms (5).

In some sense, structure - functional structure in a teleological sense, as op­ posed to mere crystalline shape - must also be considered a stage, possibly in­termediate between crystallinity and in­formation strings, in the hierarchy of broken symmetries.

To pile speculation on speculation, I would say that the next stage could be hierarchy or specialization of function, or both. At some point we have to stop talking about decreasing symmetry and start calling it increasing complication. Thus, with increasing complication at each stage, we go on up the hierarchy of the sciences. We expect to encounter fascinating and, I believe, very funda­mental questions at each stage in fitting together less complicated pieces into the more complicated system and under­ standing the basically new types of be­havior which can result.

There may well be no useful parallel to be drawn between the way in which complexity appears in the simplest cases of many-body theory and chemistry and the way it appears in the truly complex cultural and biological ones, except per­ haps to say that, in general, the rela­tionship between the system and its parts is intellectually a one-way street. Synthesis is expected to be all but impossible; analysis, on the other hand, may be not only possible but fruitful in all kinds of ways: Without an under­ standing of the broken symmetry in superconductivity, for instance, Joseph­ son would probably not have discovered his effect. [Another name for the Joseph­ son effect is “macroscopic quantum-in­terference phenomena": interference ef­fects observed between macroscopic wave functions of electrons in super­ conductors, or of helium atoms in su­perfluid liquid helium. These phenom­ena have already enormously extended the accuracy of electromagnetic mea­surements, and can be expected to play a great role in future computers, among other possibilities, so that in the long run they may lead to some of the major technological achievements of this dec­ade (6).] For another example, biology has certainly taken on a whole new as­pect from the reduction of genetics to biochemistry and biophysics, which will have untold consequences. So it is not true, as a recent article would have it (7), that we each should “cultivate our own valley, and not attempt to build roads over the mountain ranges ... between the sciences." Rather, we should recognize that such roads, while often the quickest shortcut to another part of our own science, are not visible from the viewpoint of one science alone.

The arrogance of the particle physi­cist and his intensive research may be behind us (the discoverer of the positron said “the rest is chemistry”), but we have yet to recover from that of some molecular biologists, who seem deter­mined to try to reduce everything about the human organism to “only" chem­istry, from the common cold and all mental disease to the religious instinct. Surely there are more levels of orga­nization between human ethology and DNA than there are between DNA and quantum electrodynamics, and each level can require a whole new concep­tual structure.

In closing, I offer two examples from economics of what I hope to have said. Marx said that quantitative differences become qualitative ones, but a dialogue in Paris in the 1920's sums it up even more clearly:

FITZGERALD: The rich are different from us.
HEMINGWAY: Yes, they have more money.

References
1. V. F. Weisskopf, in Brookhaven Nat. Lab. Publ. 888T360 (1965). Also see Nuovo Ci- mento Sup pl. Ser 7 4, 465 (1966); Phys. Today
20 (No. 5), 23 (1967).
2. A. Bohr and B. R. Mottelson, Kgl. Dan. Vidensk. Selsk. Mat. Fys. Medd. 27,16 (1953).
3. Broken symmetry and phase transitions: L.
D. Landau, Phys. Z. Sowjetunion 11,26, 542 (1937). Broken symmetry and collective motion, general: J. Goldstone, A. Salam, S. Weinberg, Phys. Rev. 127, 965 (1962); P. W. Anderson, Concepts in Solids (Benjamin, New York, 1963), pp.175-182; B. D. Josephson, thesis, Trinity College, Cambridge University (1962). Special cases: antiferromagnetism, P. W. Anderson, Phys. Rev. 86, 694 (1952); super­ conductivity, ,ibid.110, 827 (1958)；
ibid. 112, 1900 (1958); Y. Nambu, ibid. 117,
648 (1960).
4. F. London, Superfluids (Wiley, New York, 1950), vol.1.
5. M. H. Cohen, J. Theor. Biol. 31,101(1971).
6. J. Clarke, Amer. J. Phys. 38,1075 (1969); P.
W. Anderson, Phys. Today 23 (No. 11),23 (1970).
7. A. B. Pippard, Reconciling Physics with Reali­ty (Cambridge Univ. Press, London,1972).