
Philosophiæ Naturalis-数字153と5:12:13の直角三角形-
はじめに
最近の記事はAIの記事が続いていましたので、今回は久しぶりに数字に関することを綴りました。内容は、簡単にですがリベラルアーツの四科(数学・幾何学・音楽・天文学)の繋がりを紹介するという記事です。
リアルな知り合いの中には、数学や幾何学と聞くと「難しそう」と嫌厭しがちな人が多い印象です。皆さんはどうですか?
私は友人の一人から「頭良い人アピールするな!w」と言われたことがあります。ですが私が紹介しているのは簡単な数字や幾何学。「最初から理解しようとしてないだろw」とわちゃわちゃ言い合いを経験しました。それに何か特定の思想に傾倒している訳ではなく、覆しようのない数字や幾何学が証明することを簡単に紹介しているに過ぎません。
そんな簡単な数字や幾何学から、暦や天体について繋がれば興味深く感じませんか?
私が情報発信をする上でのモットーは「なるべく分かりやすく」。ですので、今回の記事も特に難しいことは紹介していませんから気楽に最後まで読んでいって下さい。
それでは本編を見ていきましょう!
153
はじめに紹介するのは「153」という数字から。153という数字は不思議な性質を持つ数字です。例えば、1から5までの階乗の合計は153。
1!+2!+3!+4!+5!=153
また、153は自身が持つ数字だけで計算式を作ることができます。そして=を挟んで鏡のように対に。(153↔︎351)
153=3×51
他には3で割り切れる数字は全て153に帰結します。手順はそれぞれの数字を3乗し、足していくということを繰り返していくと帰結します。
それぞれの数字を3乗し足すと153に帰結する
153 → 1³+5³+3³=1+125+27=153
3で割り切れる別の数字27を例にすると
27 → 2³+7³=8+343=351
351を同じ手順で繰り返す
3³+5³+1³=27+125+1=153
このように153は不思議な性質を持つ数字です。この数字は聖書の中にも登場します。
シモン・ペテロが行って、網を陸へ引き上げると、百五十三びきの大きな魚でいっぱいになっていた。そんなに多かったが、網はさけないでいた。
聖書に登場する153匹の魚の件は、ある幾何学と関連づけられて有名です。それはヴェシカ・パイシス。

なぜ153という数字と魚、ヴェシカ・パイシスが繋がるのかというと、√3が鍵になります。

古代ギリシャの数学者にして天文学者であるアルキメデスは、「265÷153=1.7320261」と「1351÷780=1.7320512」の間が3の平方根、つまり√3(1.7320508)であると見積もりました。153の登場です。
√3は小数点以下の数字が無限に続く無理数。小数点以下の数字が無限に続くので紙などに書き表すことは不可能、√3と表記するしかありません。ですが、図形(幾何学)では書き表すことができます。幾何学は、数字を空間で表したものだからです。
ではどの様にして√3を幾何学で描くのかというと、ヴェシカ・パイシスを用います。

上の画像のようにヴェシカ・パイシスを描くことによって√3を描くことができました。アルキメデスの見出した√3の近似値を求める「265÷153」を図に当てはめるとこの様に。

153から√3、√3からヴェシカ・パイシス、と繋がりました。ではなぜ聖書の記述にある魚と結び付くのかと言うと、その形状が魚に似ているからが理由です。

ちょっとこじつけっぽく感じますか?ですが初期のキリスト教徒が使用していたイクトゥスは上の図のそれです。イクトゥスはジーザス・フィッシュやクリスチアン・フィッシュとも呼ばれるシンボル。魚と結び付いています。


これで153という数字と魚がヴェシカ・パイシスによって丸っと繋がりましたね。少し脱線しますが、魚とシンボル(象徴)についてもう少し深掘りしてみたいと思います。
マンリー・P・ホールの本の中に面白い記述があったのて抜粋します。
ナン(nun)は魚と成長の両方を意味するのであって、インマンが言っているように、「ユダヤ人は『魚の息子』、別名、ヨシュア、イエス(『救世主』)により勝利へ導かれた。ナンは今もなお」キリスト教の「尼僧を指す名である。」初期のキリスト教徒たちのあいだでは三匹の魚が「三位一体」を象徴するために使われたが、魚は偉大なブッダの聖なる八つの象徴のひとつでもある。
下の画像はトリケトラ。トリケトラはキリスト教が誕生する前から使用されている象徴ですが、初期のキリスト教徒も三位一体のシンボルとして使用していました。前述のヴェシカ・パイシスと魚の説明を理解していれば、上記引用の太字部分も理解できるかと思います。

それと本当にどうでも良く、且つ唐突なんですけど、NHKの朝ドラ『あまちゃん』でブレイクしたのんさんが、2022年公開の映画『さかなのこ』で主演とはよく出来てるなと思ったり。
だってマンリー先生の引用を見て下さいよ。「魚の息子」と映画のタイトル「さかなのこ」。
「ナンは今もなおキリスト教の尼僧を指す名である」…尼僧(あま)と海女(あま)。
「ナン(nun)」と「のん」。………なーんてねっ!

少し妄想の癖が過ぎました。ちょっとマンリー先生の本を読み返していて「あれれ?」とシナプスが繋がったのですが、考え過ぎかもしれません。

もう少し魚について付け加えると、春分点と黄道十二宮の星座が関連します。春分点は歳差運動により黄道十二宮を25920年かけて一周します。これを12宮で割れば一つの宮を抜けるのに2160年かかります。
ちなみに太陽太陰暦の二十四節気の定め方のひとつ定気法では春分点を基準としていたそうです。
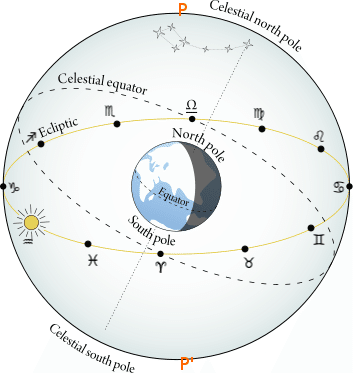
春分点が金牛宮(おうし座)にある時は牛が象徴され、白羊宮(おひつじ座)に春分点が重なれば牡羊が象徴として残されてきました。現在の春分点は双魚宮(うお座)にあるとされており、魚が象徴として使用される理由でもあります。


と、ここまで少し脱線しちゃいましたが、不思議な性質を持つ153という数字はあとからも登場しますので覚えておいて下さいね。次の章ではピタゴラスの三角と四科(数学・幾何学・音楽・天文学)を絡めつつ繋がりを見ていきましょう。
5:12:13
この章では「5:12:13の直角三角形」に視点を向けていきます。

この5:12:13の直角三角形はピタゴラスの定理に該当する三角形です。
簡単にピタゴラスの定理を説明すると、「直角三角形の三辺の間に成り立つ関係」の定理です。斜辺の長さをcとした時、直角をはさむ二辺をa,bとすると以下のような等式が成り立ちます。
c²=a²+b²
斜辺cの2乗に対して、直角をはさむ二辺a,bの2乗の和は等しいということです。そして直角三角形の二辺の長さがわかっていれば残りの辺の長さも計算できるのがピタゴラスの定理でした。
また、2乗するということは正方形の面積も得られます。私がX(旧Twitter)でたまに紹介している以下の様な画像はピタゴラスの定理によるものですね。それぞれの辺の長さの正方形の面積もまた「c²=a²+b²」。


定理の説明で「直角三角形の三辺の間に成り立つ関係」と出てきました。この関係は正に三位一体です。エジプト神話に登場するオシリス・イシス・ホルスをピタゴラスの三角に当てはめた図画を目にしますが、上のGIF画像のように父オシリス(3²=9)と母イシス(4²=16)の性質を受け継いだ子ホルス(5²=25)の三位一体の関係は、ピタゴラスの定理を準えたものです。

この章の頭で紹介した5:12:13の直角三角形に話を戻しましょう。この三角形もピタゴラスの定理に該当します。

↓
169=25+144
↓
169=169
3:4:5の直角三角形はよく取り上げられますが、5:12:13の方はあまりフューチャーされない印象です。ですが5:12:13の直角三角形も理に関係する図形です。その理に関することを四科(数学・幾何学・音楽・天文学)の視点から繋げていきましょう。

まずは金星との符合から。金星と地球の公転周期の差のために上の画像のような幾何学が描けます。太陽の周りを地球が8回公転している間に、金星は13回公転し、その間に5回の会合が起こります。

この説明は過去の記事でも何度か取り上げており、記憶にあるという方もいらっしゃるかもしれません。黄金比が見出せるフィボナッチ数列に登場する5,8,13が関係しているんでしたね。
実はそれだけでは無いんです。地球と金星の5回の会合の間、金星は13回公転しますが、12回自転もしています。
5,12,13の数字の符号が、地球と金星の会合周期が織りなす幾何学模様の背景に隠れています。
フィボナッチ数列が登場したので、そのことも絡めて見てみましょう。
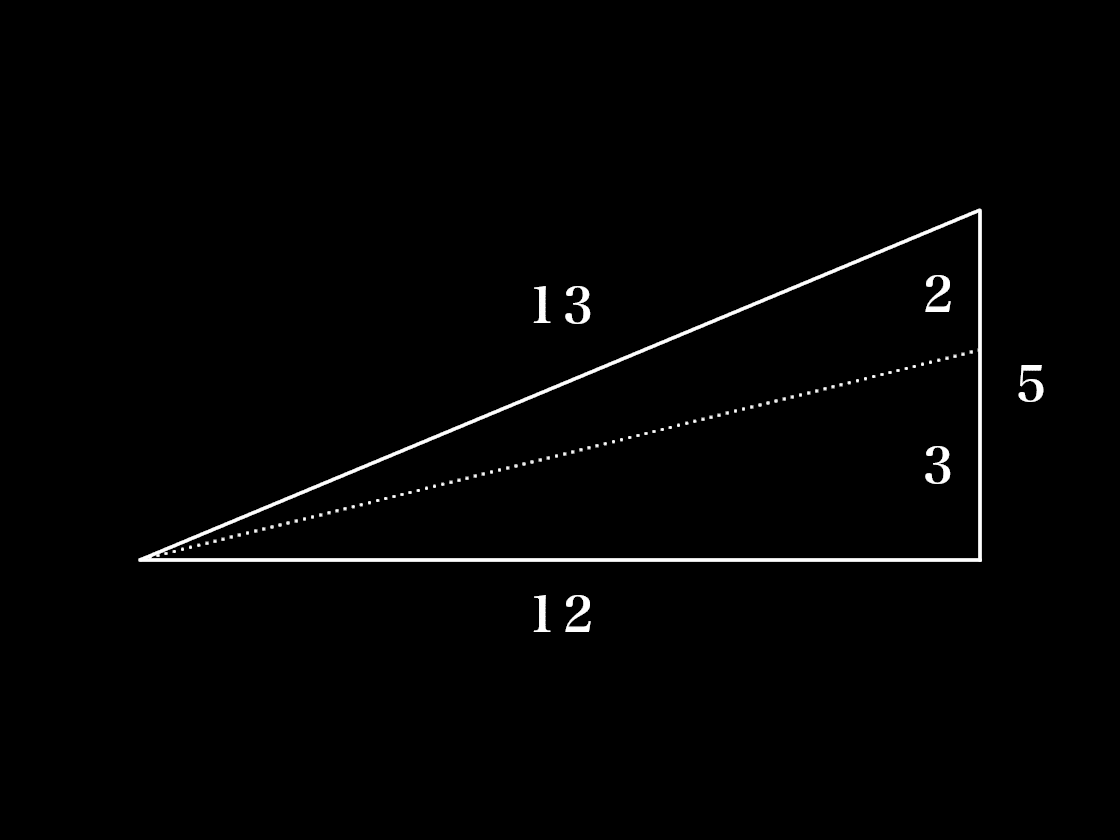
5:12:13の直角三角形の5の辺を2:3の黄金比で分割します。ちなみに、2:3の比は音楽において完全5度(例:ドの完全5度はソ。ドから数えて5つ上の音、ド→レ→ミ→ファ→ソ。ドとソの周波数の比は264Hz:369Hz=2:3)。オクターブ(2:1)に次いで基本的な和音です。

黄金比で5の辺を2:3(完全5度)の黄金比で分割しましたが、登場する数字2,3,5もまたまたフィボナッチ数列。そして音楽的に調和をみせる和音。
数学・幾何学・音楽・天文学が繋がりましたね。
そろそろ記事の文字数も多くなってきたので、最後にもう一丁紹介して締めに向かいましょう。
5:12:13の直角三角形は暦とも数字の符合を見せます。太陽暦の12か月、そして閏月を含む太陰暦の13か月。それぞれの暦での一年。
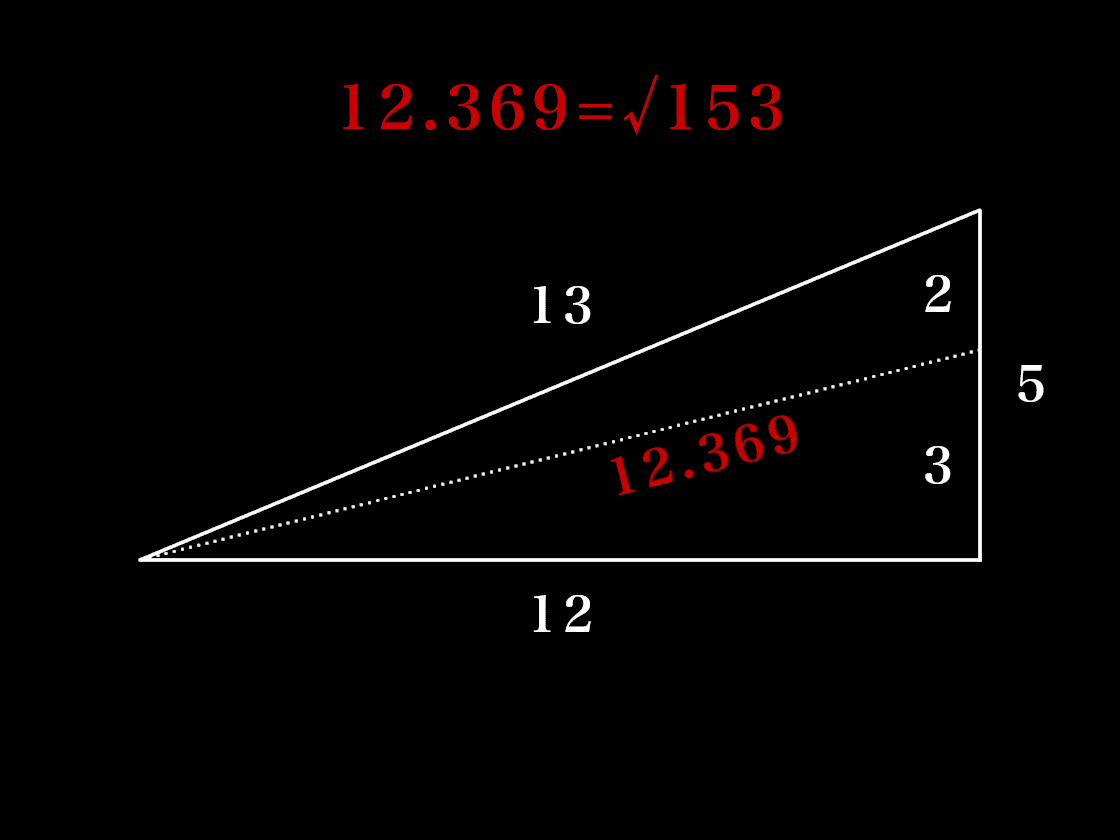
それだけではありません。先ほどの2:3の分割ポイントから鋭角に向かって線を伸ばすと、その斜線の長さは12.369になります。ちなみに、12.369は2乗するとその値は153に。前章で登場していた153が再び顔をのぞかせましましたね。そんな√153=12.369は月に関係する数字。
12.369は太陽暦において1年に訪れる満月の回数と一致します。

新月から満月までの1周期を朔望月と言います。1朔望月の長さは、およそ29.53日。
12.369回×29.53日=365.256日(1太陽年)
三位一体を成す5:12:13の直角三角形。そして月と太陽に関する数字から地球での暦までが繋がりました。
月と太陽と地球もまた三位一体。単純な幾何学から「この世の理」も読み解けましたね。
不思議な数字153から5:12:13の直角三角形、四科(数学・幾何学・音楽・天文学)は視点を合わせれば繋がっています。
おわりに
記事のはじめにで「簡単な数字や幾何学から、暦や天体について繋がれば興味深く感じませんか?」と書きましたがいかがだったでしょうか?少しでも興味深く感じていただけたら情報発信をしている者として嬉しく思います。
実はまだ今回の記事に関係することで書きたいと思っていることがいくつかあります。次の記事でもヴェシカ・パイシスとピタゴラスの定理が登場しますので、覚えておいて下さいね!
あと念のための注意として、宗教について引用をしましたが、私は特定の宗教に肩入れはしていません。それぞれの信仰について尊重しているつもりですので悪しからず。
少しでも「面白い!」と思っていただけたら励みになりますのでスキをお願いします!
おまけ

※無断での引用・転載禁止※
本記事を引用・転載されたい方はX(旧Twitter)にてメールして頂けましたら対応します。
noteプロフィールにあります、Xのアイコンからどうぞ。
