グラフ理論について（２）

みなさん、こんにちは。

今回はケーニヒスベルクの７つの橋の問題と一筆書きの定理について紹介していきたいと思います。

【１】ケーニヒスベルクの7つの橋の問題とは？

　18世紀ごろ、プロイセン王国の東部にケーニヒスベルク(現ロシア連邦カリーニングラード)という町がありました。この町の中央にはプレーゲル川という大きな川が流れており、７つの橋が架けられていました。

あるとき、町の人が言いました。

「このプレーゲル川に架かっている７つの橋を2度通らずに、全て渡って帰ってくることはできるのだろうか？」ただし、どこから出発してもよい。

さて、町の人が言ったことはできるのでしょうか。

1736年、オイラーは、この問題をグラフに置き換えて考えました。

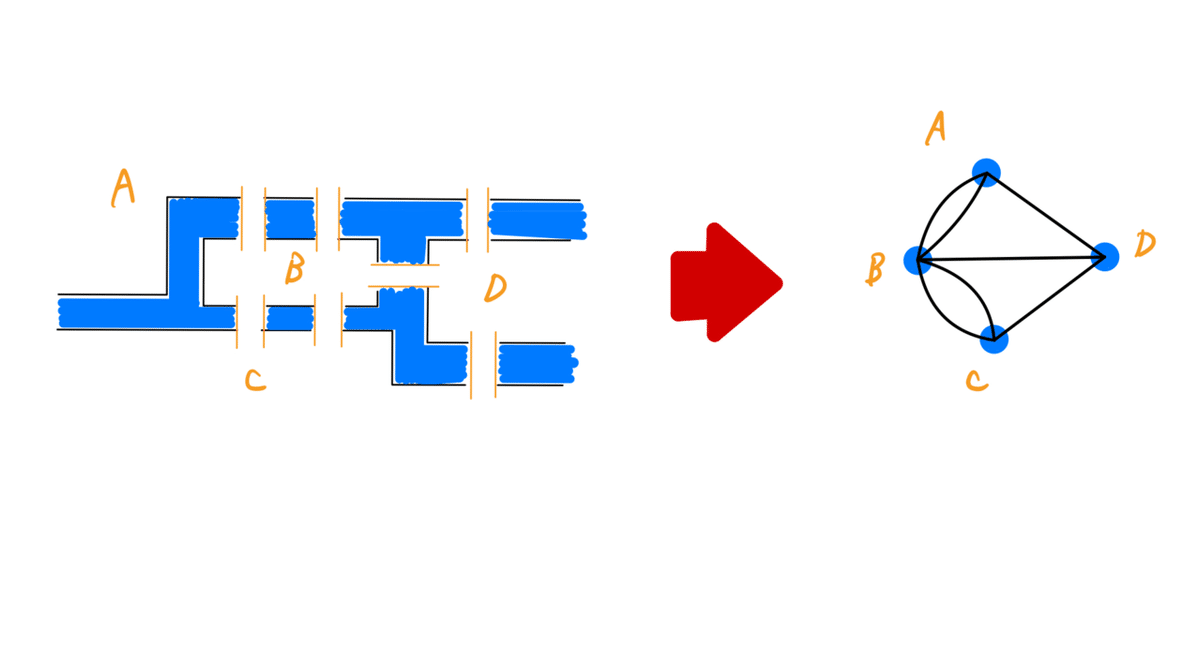
つまり、このグラフが一筆書きすることができたら、ケーニヒスベルクの７つの橋を全て渡って帰ってくることができる。ということである。

オイラーはグラフを用いてケーニヒスベルクの７つの橋を全て渡って帰ってくることはできないという結論を出しました。

では、オイラーはどのようにして、このような結論に至ったのでしょうか。

【２】一筆書きの定理

※今回扱うグラフは広義グラフを用います。

一筆書きの定理
グラフは次のいずれかを満たすとき、一筆書きすることができる。
①グラフの全ての頂点の次数が偶数である。
②グラフにちょうど2個だけ奇数の頂点がある。

また、①を満たすとき、そのグラフをオイラーグラフといい、②を満たすとき、そのグラフを半オイラーグラフといいます。

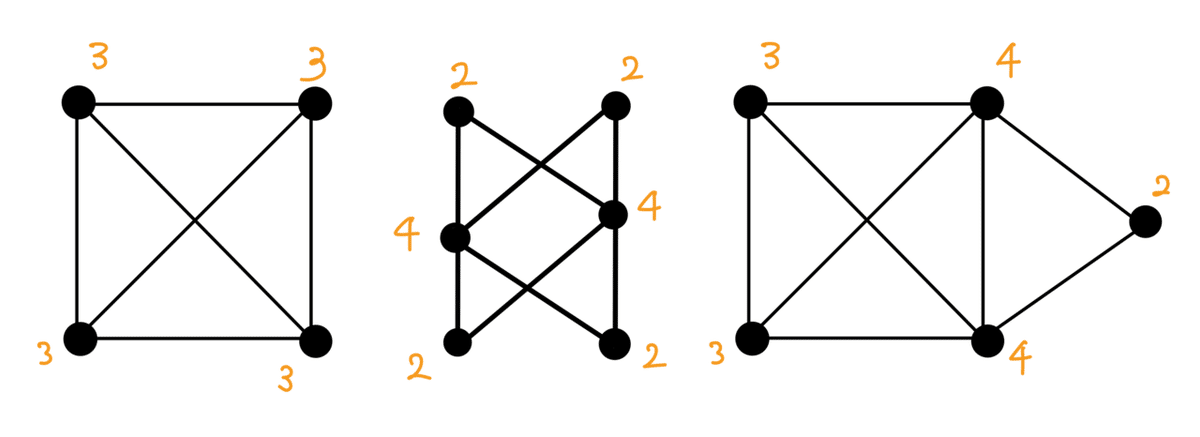
左側の図形は次数が奇数である頂点が４つあるので、①②を満たしません。
よって、一筆書きできない図形になります。

真ん中の図形は全ての頂点の次数が偶数であるので①を満たします。
よって、一筆書きできるオイラーグラフとなります。

右側の図形は次数が奇数である頂点がちょうど２つであるので、②を満たします。よって、一筆書きできる半オイラーグラフとなります。

ちなみに、半オイラーグラフのときは、次数が奇数である頂点からスタートし、次数が奇数である頂点がゴールになります。

【３】ハミルトングラフについて

オイラーグラフは全ての辺を1回だけ通って一筆書きできるグラフでしたが、ハミルトングラフは全ての頂点を1回だけ通って一筆書きできるグラフになります。

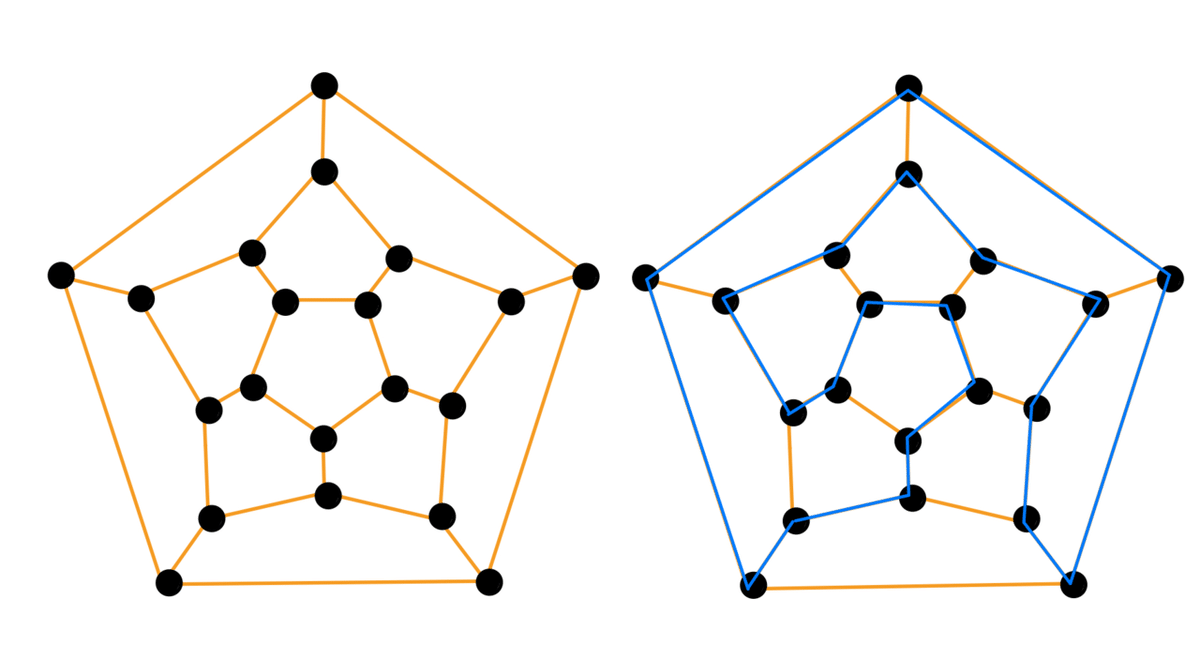
左の図のグラフは右の図のように全ての頂点を通って一筆書きすることができます。このようなグラフをハミルトングラフといいます。

【４】最後に

今回は一筆書きできるグラフについて紹介しました。

次回は、オイラーの多面体定理について紹介していきたいと思います。