グラフ理論について（５）

みなさん、こんにちは。

今回は四色問題について紹介していきたいと思います。

【１】四色問題とは何か？

まずは四色問題について紹介します。

四色問題
4色あれば、どんな地図でも隣り合う国々が違う色になるように塗り分けることができるのか？

地図を色分けしていくとき、私たちはごく自然に、隣り合う国々を違う色で塗り分けていきます。なぜなら、その方が区別しやすいからです。

下の図は、アメリカの州を隣り合う州を違った色になるように4色で塗り分けられています。

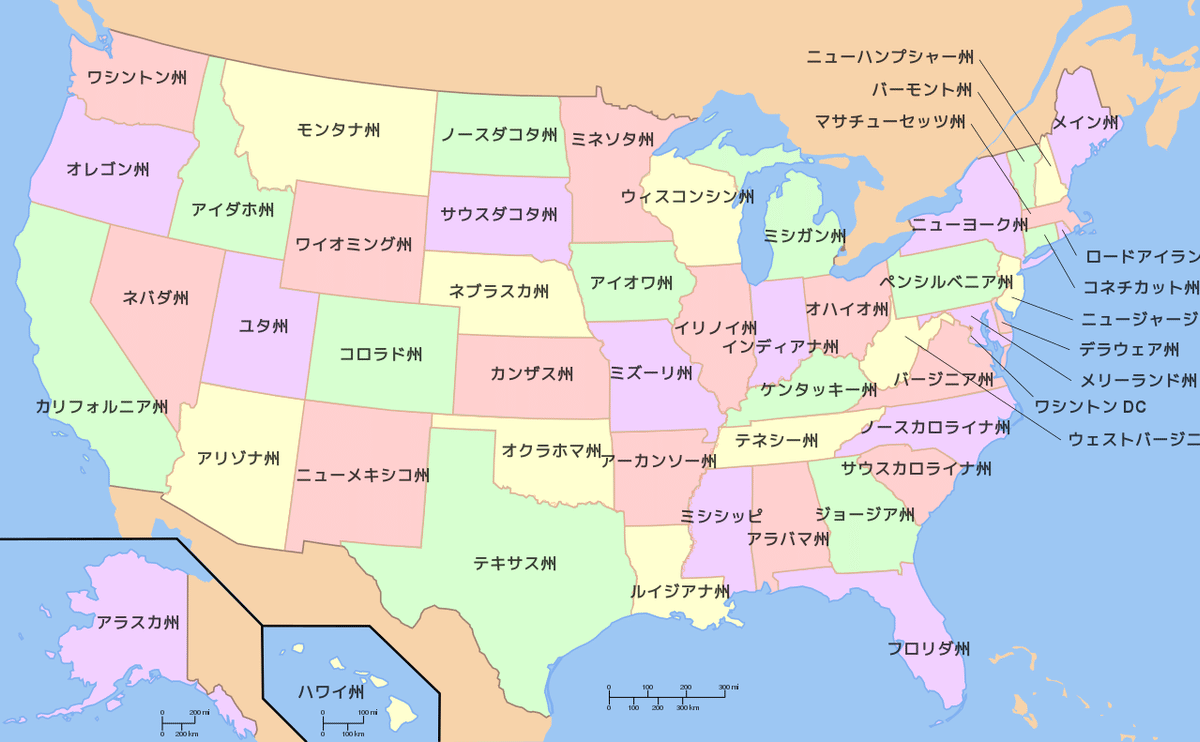
どんな地図でも、このようにたった4色で塗り分けることができるでしょうか？

一見すると、地図が複雑になればなるほど、もっと多くの色が必要になると思われる方も多いのではないでしょうか。

次に、四色問題を証明することができるのかについて考えていきたいと思います。

【２】四色問題を証明する

「四色問題を証明する」ためには、世界中の地図や、架空の地図まで4色で塗り分けることが可能であるということを示さなければなりません。

もし、この命題が間違っているのであれば、５色以上なければ塗り分けられない地図（反例）を持ってこなければいけません。

この問題は、1852年にイギリスのフランシス・ガスリーが数学専攻である弟のフレデリック・ガスリーに質問したことをきっかけに提起されました。

しかし、1２0年以上もこの問題は未解決のまま放置されていました。

最終的に四色問題を解いたのはヴォルフガング・ハーケンとケネス・アッペルであり、1976年のことでした。

彼らの方法はコンピュータに1000時間以上も計算させるというものでした。

よって、四色問題から四色定理となり、全ての地図は4色で塗り分けることが可能であるということが示されました。

しかし、人間の手で結果を直接確認することができない場合に、問題が解決されたと考えていいものかという点をめぐって、今日もなお議論が続いています。

【３】トーラスについて

四色問題を解いていくうえで、平面だけでなく、球面やドーナツのような形である「トーラス」上にも地図を描き、塗り分けるのに必要な色の数が突き止められていきました。

4色で塗り分けられた平面の地図を曲げたり、引き延ばしたりしても、その地図は4色で塗り分けられることは直感的にわかるのではないかなと思います。

つまり、平面を丸めて球面にすることもできます。

そのため、平面で四色定理が成り立てば球面でも成り立つということがわかります。また、その逆も言えます。

次に、真ん中に穴の開いたドーナツのような形を考えてみます。下のような図形です。

このトーラス上に地図を描く場合には塗り分けに7色が必要であることが証明されています。

この証明は、より単純な平面や球面よりも先に証明されたらしいです。
この定理を七色定理というらしいです。

【４】最後に

今回は四色定理について紹介しました。
コンピュータを用いない方法でこの定理を証明することができる日は来るのか楽しみですね。

四色定理の下位互換に五色定理というものもあります。

この定理は数学的に証明することができるので、気になった方はさらに調べてみて下さい。

最後まで読んでいただき、ありがとうございました。