グラフ理論について（４）

みなさん、こんにちは。

今回はパーティにおける問題を紹介し、その問題からラムゼーの定理を導いていきたいと思います。

【１】パーティ問題とは？

パーティ問題
6人でパーティーを開いたとき、その6人にはお互いに知り合いの3人が存在するか、またはお互いに知り合いではない3人が存在する。

この問題(命題)を証明する道具として、完全グラフをつかいます。

今回は6人ですので、K₆をつかいたいと思います。

【２】パーティ問題の証明のための準備

まず、6人をそれぞれ、Aさん、Bさん、Cさん、Dさん、Eさん、Fさんとします。K₆のグラフの頂点に、それぞれAさんからFさんまでを対応させて考えていきたいと思います。

次に、A～Fさんが知り合いであれば赤い線、知り合いでなければ青い線で結ぶことにします。

最後に、赤い三角形もしくは青い三角形が必ずできることを証明することでこのパーティ問題を証明することができます。

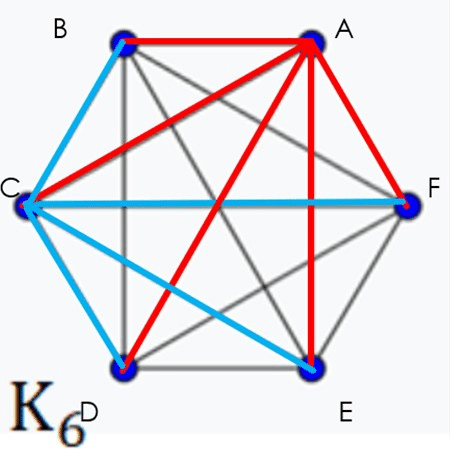
上の図では、Aさんが他の5人とは全員知り合いで、CさんはAさん以外の4人とは知り合いではないときを表したものです。

このような図を用いて考えていきたいと思います。

【３】パーティ問題の証明

いろいろなパターンに分けて考えていきたいと思います。

（証明）

まず、点を1つ決める。
その点からは5本線を引くことができるので、
その線を赤と青で分けるとすると、
(ⅰ)赤い線が５本、青い線が０本
(ⅱ)赤い線が４本、青い線が１本
(iii)赤い線が３本、青い線が２本
(Ⅳ)赤い線が２本、青い線が３本
(Ⅴ)赤い線が１本、青い線が４本
(Ⅵ)赤い線が０本、青い線が５本
の６パターンが存在する。
しかし、（Ⅳ）（Ⅴ）（Ⅵ）は（ⅰ）（ii）（iii）と赤い線と青い線の数を交換しただけである。
よって、この（ⅰ）（ii）（iii）の3パターンについて考えていく。

(ⅰ)赤い線が５本、青い線が０本
Aから赤い線を5本引く。
次にBに注目する。BからC～Fに赤い線を引くと、赤い三角形ができる。
また、BからC～Fに青い線を引く。
次にCに注目する。すると、CからDに対して赤い線を引いても、青い線を引いても赤い三角形もしくは、青い三角形を作ることができる。
他の点を選んだ時でも同様に成り立つ。

(ⅱ)赤い線が４本、青い線が１本
Aから赤い線を４本、青い線を1本引く。
次にBに注目する。BからC～Eに赤い線を引くと、赤い三角形ができる。
また、BからC～Eに青い線を引く。
次にCに注目する。すると、CからDに対して赤い線を引いても、青い線を引いても赤い三角形もしくは、青い三角形を作ることができる。
他の点を選んだ時でも同様に成り立つ。

(ⅲ)赤い線が３本、青い線が２本
Aから赤い線を３本青い線を2本引く。
次にBに注目する。BからC、Dに赤い線を引くと、赤い三角形ができる。
また、BからC、Dに青い線を引く。
次にCに注目する。すると、CからDに対して赤い線を引いても、青い線を引いても赤い三角形もしくは、青い三角形を作ることができる。
他の点を選んだ時でも同様に成り立つ。

以上、（ⅰ）～（ⅲ）より、

6人でパーティーを開いたとき、その6人にはお互いに知り合いの3人が存在するか、またはお互いに知り合いではない3人が存在する。　（証明終了）

【４】ラムゼーの定理とは？

ラムゼーの定理
A,B は任意の定数とする。頂点数 nの完全グラフの枝を赤と青に塗り分けるとき，nが十分大きければ 「頂点数 A の赤い完全グラフ」または「頂点数 B の青い完全グラフ」が必ず存在する。この条件を満たす最小の n をラムゼー数と呼び，R(A,B)　と表す。

先ほどのパーティ問題によって、R(３,３)≦６であることが示されました。

上の図より、K₄ や K₅ のときは「頂点数 3 の赤い完全グラフ」または「頂点数 3 の青い完全グラフ」が存在しない場合があるため、R(３,３)＝６であることが分かりました。

他にも、R(１,１)＝R(１,２)＝R(１,３)＝・・・＝１
R(２,２)＝２　R(２,３)＝３　R(２,４)＝４　・・・R(２,ｎ)＝ｎ
R(３,３)＝６　R(３,４)＝９　R(３,５)＝１４　R(３,６)＝１８　R(３,７)＝２３
R(３,８)＝２８　R(３,９)＝３６
R(４,４)＝１８　R(４,５)＝２５

以上にあげたラムゼー数については計算されており、確定していますが、
R(５,５)などについては、まだ答えが確定しておりません。

ラムゼー数を決定するにはとても難しいということが分かりますね。

【５】最後に

今回は、パーティ問題とラムゼーの定理について紹介しました。

次回は、4色定理について紹介ていきたいと思います。

最後まで読んでいただき、ありがとうございました。