
大きなお口のシグマくん:シグマくん分身の術
おやつもジュースも買いたい!
前回は、5人の子どもにおやつを選ばせたが、今度はジュースも選ばせてみよう。こんな感じに選んだことにして、話を進める。
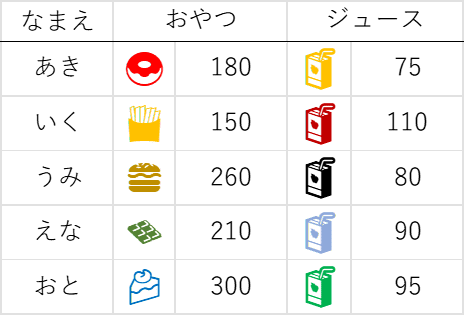
シグマくんの助けを借りて、合計の値段を計算することを考える。細かいことだが、合計の計算の仕方は、2つのやり方がある。

右の方法(1)は、子ども一人ずつ、「おやつセット(おやつ+ジュース)」の値段を計算し、それを5人分合計するやり方。
左の方法(2)は、おやつの合計、ジュースの合計を計算しておいて、それを足し合わせるやり方。
結果は当然同じになる。が、(2)の方が断然良い。このことについて、シグマくんにお口をあいてもらって、その中に数を入れて考えてみよう。

この書き方で間違いないのだが、(2)の計算方法にしたがえば、次のように書き表すのがより良いだろう。つまり、

そう、おやつの合計を計算するシグマくんと、ジュースの合計を計算するシグマくんに「分身!」する。こうすると、あとから足し合わせる計算は1回で終わる。これを、数式チックに表現してみよう。
$$
\sum_{i=1}^5\big( おやつ_i+ジュース_i \big) = \sum_{i=1}^5 おやつ_i + \sum_{i=1}^5 ジュース_i
$$
等号の左側は、おやつとジュースの値段を全部入れ込んだ式。
右側は、シグマくんが「おやつの合計」と「ジュースの合計」に分身した式。
大事なことを少し補足すると、等号の左側で、おやつとジュースがカッコでくくられていることは大事。たとえば $${i=1}$$ のとき、おやつ1とジュース1の値段を合計して(これを $${i=5}$$ まで全部やって)、それらを合計するから、ここにカッコが必要。カッコがないと、おやつだけを合計して、$${ジュース_i}$$たちが置き去りになってしまう。
では、もう少し一般化しよう。ここでは、おやつとジュースだったが、シグマくんに計算してもらう数はなんだっていい。だから、とりあえず $${x}$$ とか $${y}$$ とか書いておく。
$${\sum_{i=1}^n (x_i+y_i) = \sum_{i=1}^n x_i +\sum_{i=1}^n y_i}$$
この $${x}$$ とか $${y}$$ には、2つまとめて合計したい数なら何でも入れていい。たとえば、「数学の点数と物理の点数」とか(理系的能力が現れそうだね)、「料理をした時間と子どもの世話をした時間」とか(家事に費やした時間がわかりそう)だ。
2つができるなら、3つだって4つだってできる。5教科の点数を全部合計しよう、とか、幸福感について尋ねた10個の質問の答えを合計しよう、とか。
ここまでがわかると、次の「シグマくん消える!」が容易にわかるようになると思う。なぜ消えるか、どう消えるかがわかると、あの忌まわしき「分散公式」を追いかけることができるようになる。がんばろう。
