
大きなお口のシグマくん(3):シグマくんが消える話
シグマ(Σ:総和記号)の考え方についての3回目だ。前々回は、シグマは要するに足し算の筆算だよ、ということ、前回は、シグマは分身の術を使うよ、ということを書いてきた。今回はその延長で、シグマが消える話。
ジュースは同じやつにしてね
前回までは、おやつとジュースを好きに選んでもらっていたが、今回は、「悪いけど、ジュースはみんな同じやつにしてね」というパターンを考える。おやつだけ自由に選んでもらって、ジュースは同じのを選んでもらう。表にするとこんなふう。
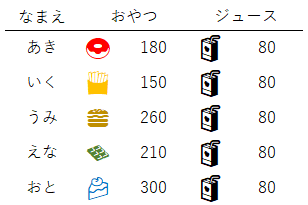
シグマくんの助けを借りて、この合計の計算をしよう。前回と同じように考えると、こんなふうになるだろう。

これでよし! と思いたいのだが、ちょっと待て。2つ目のシグマって、もっと簡単になるんじゃね? だってさ。
前回みたいに、計算方法を図解してみると、こうなるでしょう。

シグマくん分身の術の説明で使ったのは右側の図。ジュースはみんな80円のを選んでもらっているから、$${80+80+80+80+80}$$ でもいいけど、どっちかというと、$${80\times5}$$ で計算するよね?
シグマくん呼ぶ必要、ある?
ない。
というわけで。

分身の術で2つに分かれたシグマくんのうち、2つ目の方、つまり、「同じ数をひたすら足す」のほうは、掛け算にできる。なので、シグマくんにお帰りいただいて、掛け算にした。
どう書き直すかというと、シグマくんのなかに出てくる数(全部同じ)に、シグマくんの肩にくっついている $${\sum_{i=1}^5}$$ の「5」を掛け算すればいい。 $${\sum_{i=1}^5}$$ は、データが1~5まであって、「とりあえず番号付けといたから」というような意味なので、この「5」を見ると、「あ、データは5つあるんだな」ということがわかる。だから、「 $${\times 5}$$ 」 とすればいい。
数式っぽくすると
数式ぽくすると、こうなる。
$$
\sum _{i=1}^5 \big( おやつ_i + ジュース \big) = \sum _{i=1}^5 おやつ_i + 5\times ジュース
$$
等号の左側、ジュースに「i」が付いていないことに注意しよう。これは、「i」が変わっても「ジュース」の値段が変わらないから。
もし、子どもによってジュースの値段が変わるなら、「ジュース」にも「i」をつけないといけない。そうしないと、誰のジュースか分からないから。でも、今回は、みんなが同じジュースを買っているので、区別する必要がない。だから、「i」をつけない。
等号の右側、ジュースの前に「5×」がついているのが、今回の「シグマが消える」のお話で説明したことだった。もちろん、「ジュース×5」と書いたって良い。
さらに、左側にはあった、カッコが消えていることに注意しよう。
左側にはカッコがあったので、カッコの中を計算してから合計した。右側にはカッコがないので、シグマくんの仕事は「+」記号の前までで終わっている。つまり、おやつの合計を計算するまでで、シグマくんの仕事終わり。
これは結構重要で、「どこまでがシグマくんの仕事なのか」を、よく注意して式を見よう。シグマくんのすぐ後にカッコがあったら、カッコが終わるまで。そうでないなら、+とか-とかの演算記号が現れるまで。
え? ×とか÷があったときはどうするん?
というモヤモヤもあると思うので、それについてはもう1つ、別の記事を書くことにしよう。
