
中学校までに学ぶデータ処理スキルまとめ
Cover Photo by Wim van 't Einde on Unsplash
中学校学習指導要領から、数学D領域の内容を読み解いてきました。そこで扱われているスキルを系統別にまとめたものが次の図です。小学校のスキルをまとめたものに、中学校で扱うスキルを付け加えて図示しました。分類は(1)データの集計(2)データの可視化(3)代表値(4)確率 の4つに加えて、(5)標本調査 を付け加えています。順に整理します。
なお、小学校でのスキルのうち、中学校との関連の薄いものをいくつか省いています。また、学習する学年ではなく領域別に、A:資料の整理(データの分布)、B:確率(不確定な事象の起こりやすさ)、C:標本調査としています。A、Bは中学1・2年、Cは中学3年の内容です。
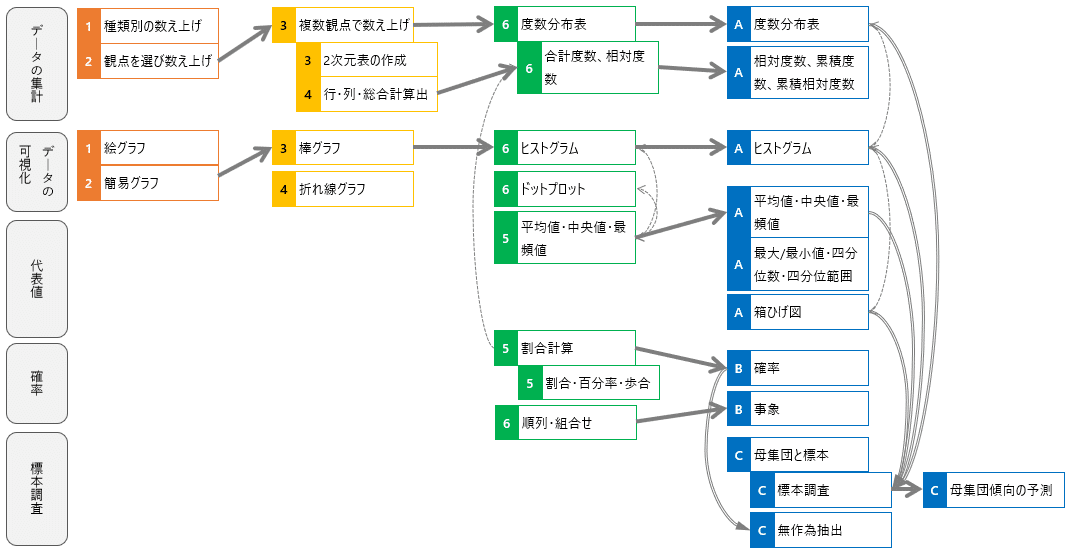
データの集計と可視化、代表値
この領域では、小学校で学習した、度数分布表、ヒストグラムに加えて、新たに箱ひげ図を学習します。箱ひげ図を描くためには、四分位数および最大値、最小値の理解が必要ですから、それらも学習します。
それに加えて、図には描き入れていませんが、値を比較するという学習が増えてきています。たとえば、
あるカテゴリ変数に対して、Nの異なる2つの度数分布表があり、度数ではなく相対度数で比較する。(1組40人と2組35人で、テストで80点以上とった生徒の割合=相対度数はどちらが多いか、など)あるいはヒストグラム同士で同様の比較を行ったり、累積相対度数の比較を行ったりする。
2組のデータがあり、平均値あるいは中央値を比較する。また、1つのデータをあえて隠して提示し、平均値が等しくなるように隠したデータの値を決める。
などです。
また、度数分布表とヒストグラムの関係だけでなく、ヒストグラムと箱ひげ図の関係を問う問題も出されています。ヒストグラムを見て、最大値・最大値、中央値、分布のひろがり等を読み取り、それを箱ひげ図に置き換えるわけです。これは結構難しい作業だと思います。
確率
確率の学習は、「注目する事象の数÷全事象の数=割合」という関係を理解することがまず求められます。試験問題などを見ていると、この「事象の数をいかに正確に数えるか」で、問題の難易度が決まっているように見えます。
また、図には書ききれませんでしたが、「ある事象が絶対に起こらない確率」も取り上げられています。つまり、「全事象」が起こる確率は1であることを理解した上で、ある事象が起こる確率をそこから引き算する、という処理が求められるわけですね。
中学校で学習する確率の内容はここまでで、和集合の確率や積集合の確率、あるいは条件付き確率などは、高等学校以降の内容です。
標本調査
中学校の内容でもっとも抽象度が高いのは「標本調査」の学習でしょう。アンケートをとって集計する、という程度の学習は小学校でもしていますので、実際にそうした活動をすることはできると思います。
が、難しいのはまず用語でしょう。「母集団」「標本」「無作為抽出」とか。用語でつまづく生徒は多そうな気がしますね。そもそも人間にアンケート調査をするのになんで「標本」? 昆虫採集じゃあるまいし! とか思う生徒もいるかもしれません。英語の sample の訳で「標本」なのでしょう。(ただし英語版Wikipediaでは Sample ではなく Sampling(statistics) を見出し語にしています。)Wikipediaを貼っておきます。
もう一つ重要なのは、標本調査(あるいは擬似的な調査)を行ったうえで、その結果を集計し、可視化し、代表値を算出して、結果を報告するという学習が求められています。その上で、標本抽出の方法は適切だったか、代表値の選び方は適切か、調査から何がわかったのかなど、批判的な考察をすることも求められています。これまでの、可視化や代表値の学習をすべて使って、総合的に問題解決する活動ですね。
このあたりは、指導する教師の工夫がおおいに必要なところだと思います。また、大学生が実際に卒業研究や修士論文などに取り組む際にも、かなり悩む部分だろうと思います。何を知りたいかによって、調査する対象も調査内容も異なります。取得したデータによって効果的な集計や可視化は異なるでしょう。よって、必要な分析手順も異なります。ここに、統計学習の難しさの一つがあると、私は思います。教科書を学習することと、それを自分の研究に応用することの間に、越えなければならない壁がいくつもあるのです。
義務教育を終えた生徒たちが、「ああ、統計って、案外面白いかも」と思ってくれることを願うばかりです。がんばれ、中学生。がんばれ、中学校の先生たち!
