見出し画像

【復活】数学科を出てみたらドット絵がこう見えた[ドット絵 Advent Calendar 2021]

ｶﾉｺﾘﾝﾀﾛｳ (Meno)

※本記事は消滅した自サイトのブログに投稿していた、ドット絵アドベントカレンダー2021へのエントリー記事の復元になります。

概要

今回の記事はドット絵 Advent Calendar の一環となっております．

学生時代に数学をかじっていた筆者が，なにを思いながらドット絵を嗜んでいるか書きます．ポエムです．でも面白がっているところを見せることが，面白さを伝える手っ取り早い方法だと思っています．ドット絵って面白いですよね．

じゃ，イラスト多めで行きます．よろしくお願いします．

12月17日はロックマンの何十何年だかの記念日だそうで，クリスマス仕様のロールちゃんにお越しいただきました．周年記念おめでとうございます．実況プレイ動画でしか見たことないけど．

名乗り忘れていました．鹿子倫太郎 (ｶﾉｺﾘﾝﾀﾛｳ) です．しがないエンジニアかつひよっ子クリエイターです．

それはそうと．

ドット絵に馴染みのない方には，このロールちゃんのイラストはどう映るのでしょう．

・・・線がガタガタ?

以前に身内に「ドット絵ってガタガタやん」と言われたことがあり，なるほどそういう意見もあるかとショックを受けたものです．

また別の意見．それは画風のモンダイ．

確かに，四角いドットでがんばって曲線を描こうとするわけですからね．縦線か横線しかない，斜め45度の線すら引けない世界です．滑らかな曲線を描こうにも限界がある．

色んな角度の直線．ガタガタね，分かる．

というのもドットの並びって，平面をマス目状に分けたときに各マス目が塗られているか，いないかの1か0しかない．中間の値がないという意味で離散的なんですよね．離散の反対は連続ですが，曲線は連続的な操作で描かれるものなので，これらの性質はまったく違います．

曲線．ドットを一定の規則で並べて表現します．白い数字は四角の面積．


この，通常のイラストで用いられる「曲線」とドットの違いの部分に，もう少し焦点を当ててみます．

どっからがドット絵?

これは等倍で見た場合のロールちゃんです．このぐらい遠目に見たら，さすがにガタガタは気にならないんじゃないでしょうか．ドットの四角が点にしか見えないぐらい，引きで見てますから．

でも，小さすぎますよね．日ごろ自分が時間をかけて描いているイラストの，何と小さいことか．

「等倍」ってどういうことかというと，ディスプレイは光の点の集まりなわけですが，この光の点1つ=ドット1つになるような縮尺ということです．(
Retina ディスプレイとかだとちょっと違うのかも．詳しくありません．)

ところで，ディスプレイも点の集まりなんですよね．

あ，で思い出すのは「デザインあ」ですね．（とくに関係のない話題）

当初この記事は「どっからがドット絵なのか」というテーマで書こうかと考えていました．

どっからがドット絵ってどういうこと?(いま「ど」って何回言った?) と思われるかもしれませんが，ディスプレイに写っているかぎり，極論すればどんな画像もドット絵だろう，というのはちらほら耳にする話です．

デザインあ，といえば，やくしまるえつこさんの「やじるしソング」ですね！（とくに関係のない話題）

こちらの見慣れた非・ドット絵フォント．

拡大するとドットの集まりでできていることが分かります．

そもそもディスプレイは，ドット(ピクセル) というごく小さな点の集まりでできているので，ディスプレイに写っている以上それはドット絵(=ドットの集まりでできた画像) である，という見方も一理あるわけです．

でも，後者のフォントをピクセルフォントとかドット絵フォントとは，まぁ言わないですよね．

じゃあ，ディスプレイに写った画像のどこからをドット絵と言うのだろう，ということです．

うちのドットネコHackle くんは，だいたいいつも何かに驚いています．

ディスプレイ上に写っていながら，どこまで拡大してもガタガタしない曲線も存在します．それがベクター画像(SVG) です．

ドット絵の対義としてのベジェ曲線

実はドット絵に次いで好きなものがベジェ曲線です．ベジェ曲線はどれだけ拡大しても滑らかだからです．

Adobe のIllustrator (イラレ) ではベジェ曲線でベクター画像が描けますが，イラレはベジェ曲線を拡大する都度，連続関数を計算しています．

連続関数っていうのはグラフで表したときに繋がっているということです．ブツブツしていない．

「連続」という概念はドット絵と対極にあると考えられます．

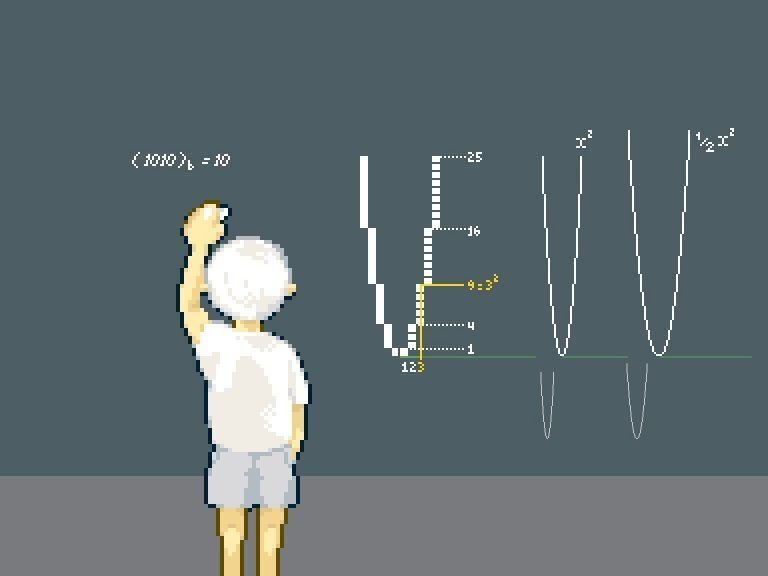
高校数学で微分積分をかじった方は見覚えがあるかもしれませんが，積分で面積が求められる理由を説明するこんな図解．

面積を求めたい部分をn分割します．


nの値をだんだん大きくします．


nが無限になったとき，青い棒の面積の足し合せ(=積分)が求めたい面積になります．


グラフもっと，きれいに書く方法あっただろって，思います．

ここまでお目通しくださった皆さんは，n を無限に飛ばす前のこの状態が，ドット絵っぽく見えてきませんか．(筆者には見えません．)

連続関数はさしずめ，この「n を無限に飛ばす」という操作と同じ要領で定義されます．

つまり「n を無限に飛ばす前の状態」がドット絵で，「n が無限に行ったときの状態」がベジェ曲線なわけです．

そう，胡散臭い話をしているんです．

そのように考えると，ドット絵が一般的な曲線からかけ離れているように映るのではないでしょうか．

n がドットの数だと思えば，これをどれだけ打ったところで，有限回の操作では，決して曲線に辿りつけないのです．

曲線が無限個のドットの寄せ集めなら，イラストだってドットより曲線を用いたほうが，自由自在に無限の表現が叶うのかもしれないですね．

ドットで表現できるイラストなんて，曲線と比べたら遥かに乏しいのかもしれません．

あれ，ほんとうにそうでしょうか．


「君，ドット絵やってて面白いん?」

時間をかけても小さい絵でしかない，斜めの線も引けない，n も無限に飛ばせない，ドット絵．

それが制約された条件のもとで，はっとするような奥行きや質感を表現することがあります．

もうすぐクリスマスですね．サンタです．それはさておき．

手元を見てみてください．下より上の方が書き込んであります．すごーく小さいですが，揃えられた指が丸みを帯びて映りませんか．

拡大するとこの通り．やっぱりガタガタ，というかもう四角が並んでいるだけで何が何だか分からないぐらいです．それが実は手を表し，指の丸さを表すものになっている．

あるいは，目．

濃い色を一点打つだけで，瞳がキラリと光るように感じたり，


ちなみにICOの記念絵でした．20周年!!

隣りあうドットのコントラストによって，突然に深い奥行きを見せたりする．

有限のドットたちが，極限の滑らかさや無限の奥行きを表現している．

離散と連続が融合している．

こう感じられる瞬間がとても面白いのです．

要するに

当たり前ですが大きい絵を描こうと思えば描けます．

今年はダイパリメイクもありましたね

大きければ制約はそれなりに薄くなりますよね．ドット絵「らしさ」も薄くなりますが．どちらかと言うといつぞやのお絵描き掲示板みたい

あるいは逆に，あえてドット絵「らしさ」を強調してスーパーデフォルメされた状態で描かれるドット絵もありますね．

サイズ別にドット絵を紹介されている，こちらの記事がとても面白かったです．

あとは，ドット絵らしさを残して独特のイラストを制作されているこちらの記事も興味深いです．

結局，いろいろ制約があっても，ドット絵の表現の幅は他のツールと変わりなくたくさん存在するし，面白さの見出し方も同じだけたくさんあるのでしょう．

本記事を通して，そのうちの1つを皆さんにお伝えすることができていれば幸いです．

自分は数学が好きで，絵が好きで，このふたつが自分のなかで両立することはしかし難しいと感じていました．

ただふと気がつくと，ドット絵で絵を描きながら数の連続と離散について思いを馳せている自分がいて，ある種の居心地の良さのようなものを感じることがあります．

今年の夏にこの絵を描いたのを皮切りに，きちんと絵を描くということを再開しました

ドット絵という表現方法があってくれて良かった．

新年の抱負

来年はイラストの仕事にも精を出していきたいと思っています．何かピンとくるものがあったら激励いただけると嬉しいです．

自サイトのギャラリーもよろしければ．


お気をつけてお帰りください. 

ここまでお付き合いくださり，ありがとうございました．

またお会いしましょう．

明日以降のアドベントカレンダーの記事もこちらでチェック！！

裏ドット絵アドベントカレンダーも漏らさずチェック！！！

関連記事

2022年（翌年）のドット絵アドベントカレンダー記事

2023年（翌々年）のドット絵アドベントカレンダー記事


いいなと思ったら応援しよう！