センター試験 微分積分による予測
こんにちは
今日はセンター試験の数学についてみていきたいと思います
数学IIの問題です
問
(1)sinxとsin2xの大小についていえ
sin2x-sinx=2sinxcosx-sinx
=sinx 2cosx-1 ①
より
x 0 π/3 π 5π/3 2π
① 0 + 0 - 0 + 0 - 0
なので
sin2x-sinx>0となるのは
0<x<π/3 π<x<5π/3 (0<x<2π)
とわかる
(2)ソメイヨシノの開花時期について次の方法で予測せよ
ある地域では毎年3月頃 ソメイヨシノの開花予想日 が話題になる。太郎くんと花子さんは開花日時を予想する方法のひとつに 2月に入ってからの気温を時間の関数とみて その関数を積分した値をもとにする方法があることを知った。
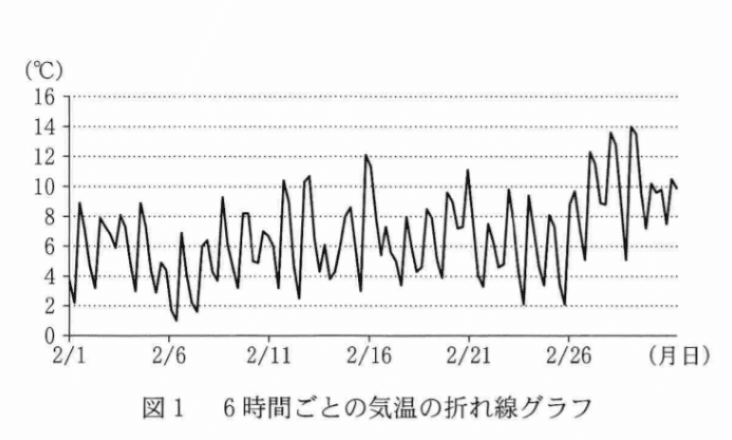
時間軸をx 縦軸の気温をy ととり
その関係をf(x)とし
y=f(x)とおく
この関数f(x)をもちいて 2人はソメイヨシノの開花日時を次の設定で考えることにした
設定
正の実数tをもちいて f(x)を0からtまで積分した値をS(t)とする
すなわちS(t)=∫0→t f(x)dxとする
このS(t)が400に達したとき ソメイヨシノが開花する
設定のもと 太郎くんは気温をあらわす関数y=f(x)を以下のように直線とみなして ソメイヨシノ開花日時を考えることにした。

太郎くんは
f(x)=1/5 x +3
として考えた
このときソメイヨシノの開花日は2月に入ってから
∫0→t 1/5 x +3 dx=[1/10 x^2 +3x]t 0
=1/10 t^2 +3t
1/10 t^2 +3t=400
より
t^2 +30t-4000=0
t=-80 50
2月に入ってから50日後とわかる
太郎くんと花子さんは2月に入ってから30日後以降の話をしている
太郎 一次関数を用いてソメイヨシノの開花日時を求めてみたよ
花子 気温の上がり方から考えて 2月に入ってから30日後以降の気温をあらわす関数が二次関数の場合も考えみようか
花子さんはf(x)を 30≦xのときは
f(x)=1/100 x^2 -1/6 x +5
として考えた
このときのソメイヨシノの開花日時を考えよう
∫0→30 f(x)dx=180
であり
∫30→40 1/100 x^2 -1/6 x +5=115
である
またx≧30でf(x)は増加する
よって
∫30→40 f(x)dx <∫40→50 f(x)dx
であることがわかる
以上から
ソメイヨシノの開花日は2月に入ってから
40日後より後 かつ 50日後より前
であることがわかる
以上です
今回とりあげたように
微分積分は実社会においても役立たされており
その例をとりあげることができ
近頃のセンター試験はすごいなと思います
