点と直線の距離
直線 $${ ax + by + c = 0 }$$と参照点$${ O = (p, q) }$$の距離$${ d }$$は、割と簡単な式で与えられている。
$$
d = \frac{| ap + bq + c |}{\sqrt{a^2 + b^2}}
$$

これの導出は様々な手法があるが、以下では参照点を原点とした座標系に変換した後、三平方と三角形の面積で導てみる。
1. 距離の式の導出
1.1 参照点を原点に座標変換
まず、点$${ O }$$との距離は、点$${ O }$$を原点とする座標系で考えると、原点との距離を求める問題に変わる。$${ (x', y') = (x - p, \, y - q) }$$ と置くと、$${ (x, y) = (x'+p, \, y'+q) }$$であるため、直線は $${ a(x'+p) + b(y+q) + c = 0 }$$になる。展開して$${ c' = ap + bq + c }$$と置けば、直線$${ ax' + by' + c' = 0 }$$と原点の距離問題になる。

右辺の「$${=0}$$」という体を保つための帳尻合わせとして、平行移動のために引いた$${ ap+bq }$$を全て$${c}$$に押し付けたと考えても良い。
$${ ax+by+c=0 }$$
$${ \Longleftrightarrow \underbrace{ax+by-(ap+bq)}_{ax'+by'}+\underbrace{(ap+bq)+c}_{c'}=0 }$$
1.2 切片の算出
こうして原点との距離に変れば、距離は切片から容易に求められる。切片が分かれば三角形の面積が分かる。切片から斜辺の長さも分かるから、面積を斜辺で割れば距離が高さとして出て来る。
切片は$${x'}$$や$${y'}$$に$${0}$$を代入すれば求められる。
$${ x' = 0 }$$のとき、$${ by' + c' = 0 }$$で、$${ y' = \displaystyle\frac{-c'}{b} }$$
$${ y' = 0 }$$のとき、$${ ax' + c' = 0 }$$で、$${ x' = \displaystyle\frac{-c'}{a} }$$
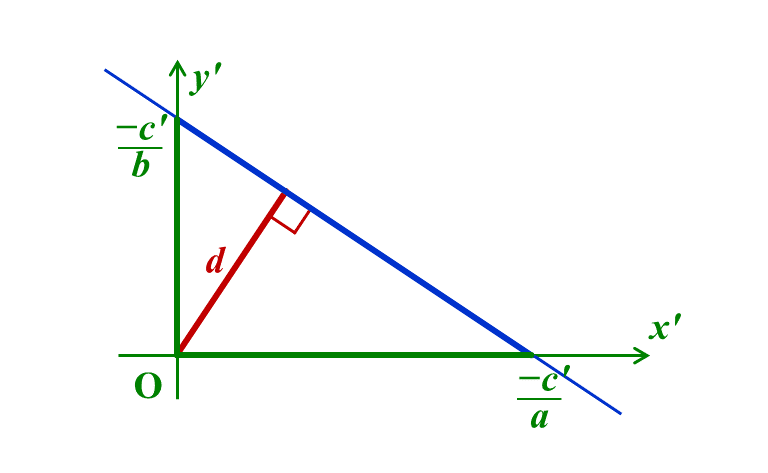
1.3 スケール変換
これで面積から距離を計算できるが、計算を簡単にするため全体を$${ k ~ = \displaystyle\frac{ab}{-c'} }$$倍にして分母を払い、$${c'}$$を$${d'}$$に集約する。斜辺は$${ s = \sqrt{a^2 + b^2} }$$になるので、斜辺に対する高さは$${ \displaystyle\frac{|ab|}{|c'|}d = \frac{|ab|}{s} }$$になる。

よって、$${ d = \displaystyle\frac{|c'|}{s} = \frac{|ap + bq + c|}{\sqrt{a^2 + b^2}} }$$
