
アクティブに使う三角関数① 太陽の1日の動きの数学モデルを作成せよ
三角関数なんていったいなんの役に立つのだろうか。そう思っているそこのあなた。私なりに答えを申し上げよう。それはあなたが使おうと思うかどうかである、と。
ということで、今回は三角関数の話だ。三角関数の応用範囲は恐ろしいほど広い。何せ周期関数といわれるだけあって周期のある事象を記述できてしまうのだ。
あの子の呼吸、あの子の歩行のリズム、そしてそこからあの子の脚の長さを逆算…おっと、妄想が暴走してしまい失礼。
とにかく色々なことを表現できる三角関数。文系の皆さんも高校のときに目にしているはず。だが果たしてこの関数を使って身の回りの事象を表現してみたことがある人はどれくらいいらっしゃるだろうか。
今回はサイン関数を用いて身近な事象を表現するコツを説明したい。皆さんはこの記事を読み終えたころには立派なサイン関数使いになっているだろう。
さて、気になるあの子の呼吸…ではなかった、身近な例として太陽の1日の動きをサイン関数の数学モデルで表現してみよう。
次の例は7月7日の太陽の位置と時刻の関係を表現している。ちなみにiPhoneの天気予報にもまさにこんな感じのグラフが入っているのでiPhoneを持っている人は携帯を見てみるといい。
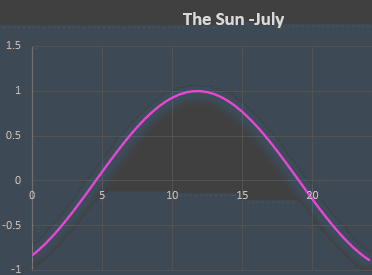
7月7日の日の入りの時刻は午前4時32分。日の出は19時01分だ。サイン関数のグラフを見るとこの両時刻においてゼロとなっていることが分かるだろう。どのように調整したのだろうか?
いきなりだが、先に数式をお見せてしまおう。調整の仕方はこの後説明する。

ん?数式を見たら吐き気が…?
ちょっと待ってほしい。行かないでほしい。ポイントはたった4つだ。
1. 関数のとる値を調整する
2. π(日の出から日の入りの時刻)を調整する
3. 関数がゼロとなる時刻を決める
4. 切片を決める
1. 関数のとる値を調整する
これはつまり垂直方向の伸縮率=sinの係数を決めるということだ。サイン関数は-1から+1の値をとる。従ってサイン関数のとる値を-3から+3にしたい場合はsinの前に係数3をかければよい。上の例では特に係数をかけていないのでサイン関数のとる値は-1から+1のままとなる。ちなみに伸縮率は最大値から最小値を引いて2で割ることで決めることができる。
2. π(日の出から日の入りの時刻)を調整する
これはつまりπにかける水平方向の伸縮率を決めるということだ。
太陽が日の入りから日の出まで移動するのにかかる時間は19.02-4.53=14.49時間。つまり関数のスタート時点である日の入りの時刻から14.49時間後が0となるように調整する。そのためにはπ自体を14.49時間で割っておく。すなわち数式のπ×1/14.49の部分である。
3. 関数がゼロとなる時刻を決める
これはいわゆる平行移動の部分であり数式中の(t-4.53)だ。日の入りの時刻午前4時32分を関数のスタート時点として設定していると考えたらよい。tに日の入りの時刻4.53を代入すると関数の値がゼロとなることからもお分かりだろう。これは日の入りのときに太陽が地平線の位置にあることを表現している。また、日の出の時刻19時01分=19.02をtに代入するとπ*1/14.49*14.49=πとなる。このときも関数の値はsinπ=0となることにお気づきだろうか。これで日の出の時刻(t=4.53)と日の入りの時刻(t=19.02)の両方でサイン関数の値が0となることが確認できた。
4.切片を決める
値域を調整したい場合は切片を設定する。これはグラフを垂直に移動する操作である。今回は設定しないが、仮に今回の例に切片+1をつけてみるとしよう。すると関数のとる値は-1から+1ではなく0から+2になる。つまりグラフ全体が上に+1移動し、値域が変わるのだ。
長くなってしまったが、以上がサイン関数をアクティブに使いこなすために必要な要素だ。イメージは伝わっただろうか。次回は気になるあの子の呼吸をサイン関数を用いて表現してみよう。
そこの数学的妄想ロマン好きのあたたは楽しみにしていてほしい。
