京都大学入試問題解説2012文系
前回の記事はこちらから
今回から京都大学の入試問題の解説を行っていきます。
第1回の問題はこちら

2012年の文系からの出題です。
点の存在範囲と三角関数の融合問題であり、受験生が苦手としているところであるかと思います。
本問では三角方程式の解が一個であり、その解が0より大きくてπ未満であることに注目して、三角方程式を解くという方針でいってみます。
では、実際に解いているところを載せます。

cosの係数が一致しているので、和積公式を使うのがわかりやすいと思います。ただ、θを求める一歩手前で場合分けの必要性が出てきます。
まずはわかりやすい方から

a=bのとき、θが消えてしまうのでこのような場合分けが必要となることに気がつきましょう。
続いて、a≠bのときを考えます。

こちらがわかりにくくて、a-bの符号によって、方程式を満たす正の解が変わってしまうことを見抜かないといけません。さらに、解を求めたあとに、0より大きくてπ未満を満たすのが一つだけをうまく式で表現しないといけません。それを表現すると次のようになります。

この解答のうまいところは方程式を満たす解以外はπより大きいと表現しているところです。個人的にはこの部分が本当の山場な気がします。
では、a<bのときもまとめておきます。

最後に領域を図示しておきます。
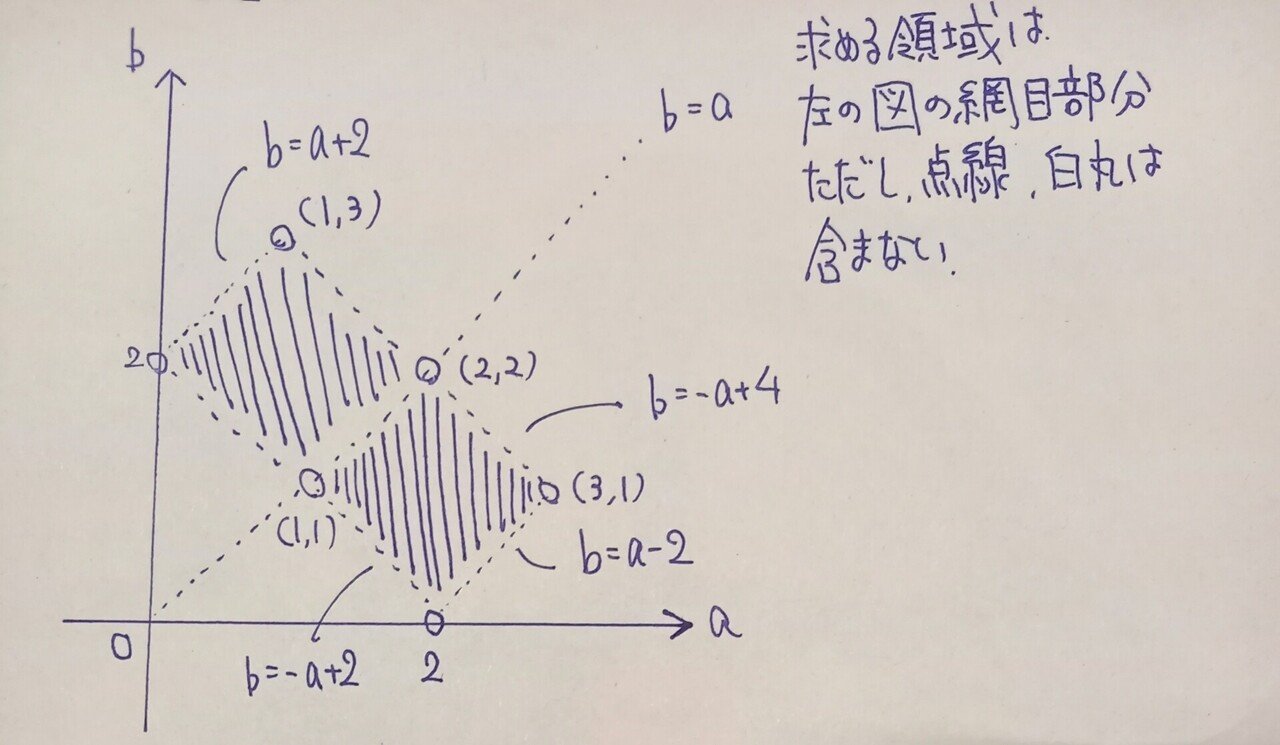
正方形が2つとなるのが面白いですね。
いかがだったでしょうか?京都大学らしく、条件を数式に具現化することが難しかったかと思います。
では、今回はここまで。また、次回を‼️
