数学力向上のヒント#3
今回も数学力向上について考えていきましょう‼️
ヒント3 数学的帰納法を使わない解法を考える
数学的帰納法は便利な解法です。しかし、それだけで終わってしまうともったいない問いはたくさんあります(当然、数学的帰納法でないとどうにもならない問いもあります)
早速、問いに入っていきましょう‼️

いかにも数学的帰納法を使う問題ですね‼️
では、その解法を紹介します。

n=kのとき、成立することを仮定して、n=k+1のとき、成立することを証明するオーソドックスな解法です‼️
ただ、不等式の解答では最後の>0を示す部分の記述が不適当なものになっていることが多いので細部までこだわって記述しましょう。
では、帰納法を使わない解法を紹介します。
ポイントになるのは二項定理です‼️
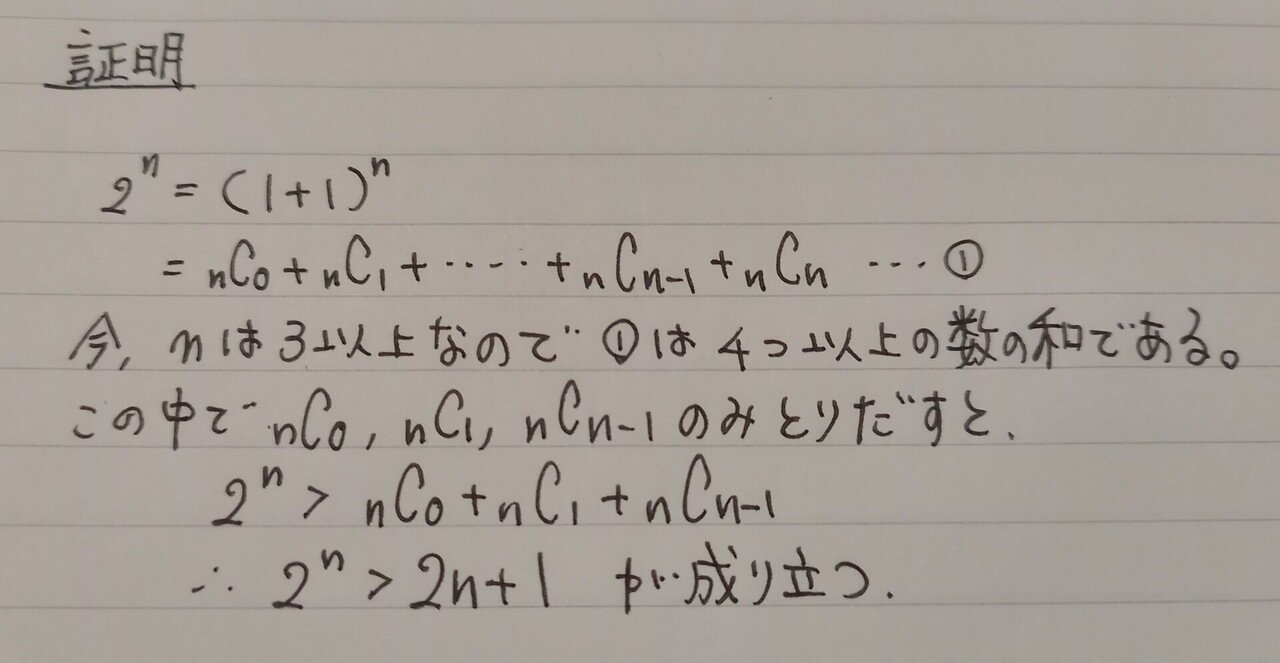
2を1+1に直すのがこの解法の肝です‼️
あとは、二項定理で展開して、必要な要素を取り出せば証明完了です。
この解法のいいところnが3以上であることの必要性が分かりやすい所です‼️なので、個人的にはこの解法が世の中の主流になって欲しいと思っています。
世の中には帰納法を使わなくても解決する問題はまだまだあると思います。皆さんもぜひ考えてみてください‼️
今回はここまで‼️また、次回お会いしましょう‼️
