共通テスト数学ⅠA整数単元解説
久々の投稿
今回は平均点が低すぎる共通テスト数学ⅠAの解説(整数単元)を行っていきます。
まずは問題から


ざっと一瞥すると答えが五桁になるところが目新しそう‼️
ということは、計算間違いを狙ってる感じ❓❓
では、早速解いていきましょう‼️
まずは(1)のア、イ、ウから

これは、簡単。5^4を2^4で素直に割ってしまえばよいだけです。実際に計算してみると

となって、不定方程式と見比べると、x=1.y=39がひとつの整数解の組となることがわかります。しかも、ありがたいことにこの1が最小の自然数なのでア、イ、ウが1.3.9であることになります。
続けて、エ、オ、カ、キ、クへ

これも簡単。ア、イ、ウを使って素直に不定方程式を解いてしまえばオーケー。解いておくと

となります。ちなみに、ここまでで、7点。個人的には不定方程式を解くだけで20点中7点取れるのはありがたいかな~
続けて(2)へ、ここから、整数らしさが出てきます。

625^2を5^5と2^5で割った余りを考える問題
5乗、2乗と目がチカチカしてくる💦
ついでに言うと、電卓を使えばすぐに解決する……
つべこべ言ってても仕方ないので解きますか…
イ、ウが活躍するようなので、625^2と39を関連付けることを意識しておきましょう。
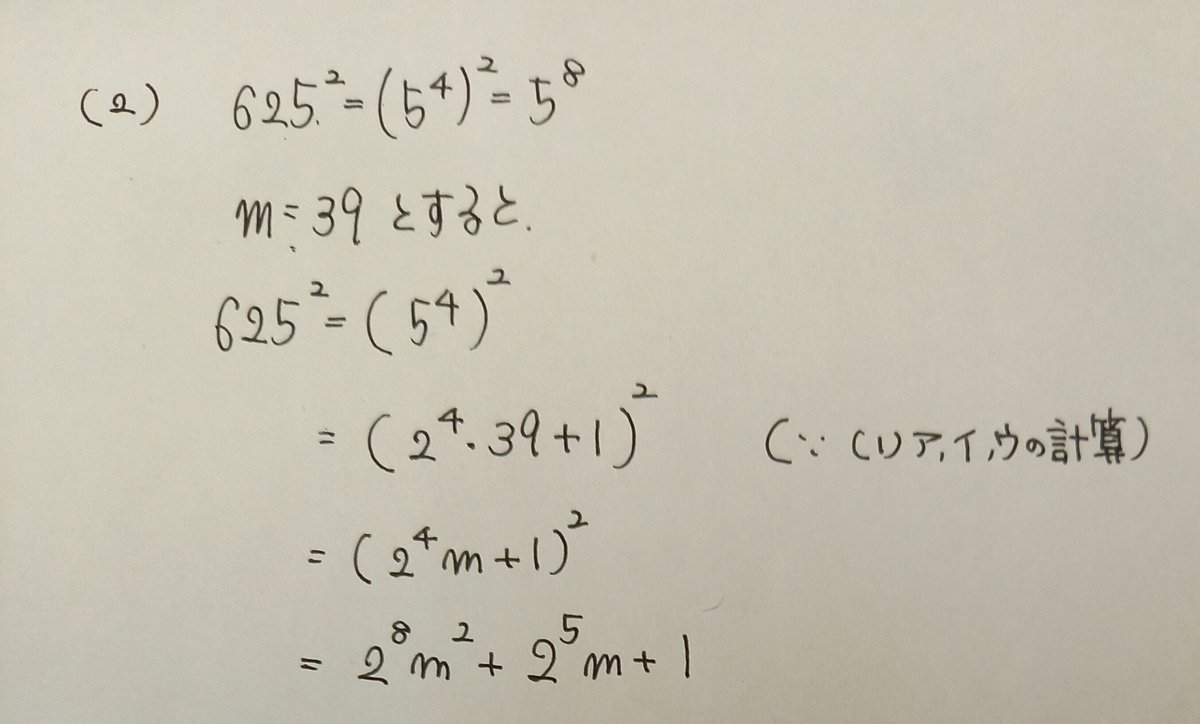
関連付けるとはいってもどうしたら…?
実は625=5^4となることがポイントとなります。
すると(1)から5^4=2^4*39+1であり、625^2と39を関連付けることができます。ここまでくれば、あっさり答えが出てきます。
あと、(2)には関係ないけど、625^2を2^5で割った余りは1となります。
ここまでで、9点。案外7点止まりの受験生も多いかもですね。
続けて(3)に入ります。

ここからが実力を試されるところ。
問題を読めばわかりますが、要するに整数解を求めたらいいだけ。
もっと極論するとユーク
リッドの互除法を使えばいいだけ。個人的には互除法を使う方が早い気がする……(笑)
誘導があるので、それに従った方法を紹介しておきます。

前置きは長いですが、要するに
5^5x-625^2=5^5*2^5*kと表せるということです。
これさえ突破すればxは125と求まります。ただ、yを求めるのが大変💦💦
一例を見せておくと……

五桁になる計算は大変💦仮に到達していても自信を持ってマークできた受験生は少ないでしょう……
最後に(4)
問題はというと

まさかの(3)と数値違いの問題‼️
(1)~(3)を真似して解きなさいと……‼️
真似して解いてみましょう

真面目に書いてみるとB5一枚丸々使いました💦
これを試験中に解ききるのはいくらなんでも厳しすぎるのでは……?しかも答えはかなり大きい数……
このような出題が続くのなら最後の問題は、はなから捨てた方が賢い戦略になりますね。
今回の問題振り返りと来年に向けての指針
・時間内に解決することは難しい→点数を取るための戦略を自分で用意しとこう
・整数単元の教科書レベルは完璧に仕上げよう→今年の問題を表現すると誘導つきの総合問題
今日はこれにておしまい
よければ👍️をお願いします
