大学入試数学今週の一題#3
学生さんはそろそろ夏休みかなぁ~?
まずは前回のおさらいから
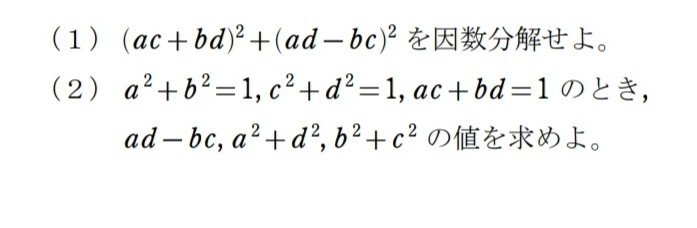
早速、(1)から。
いわゆる、ラグランジュの恒等式(プラーマグプタの二平方恒等式)と言われるものです。
サクッと証明すると
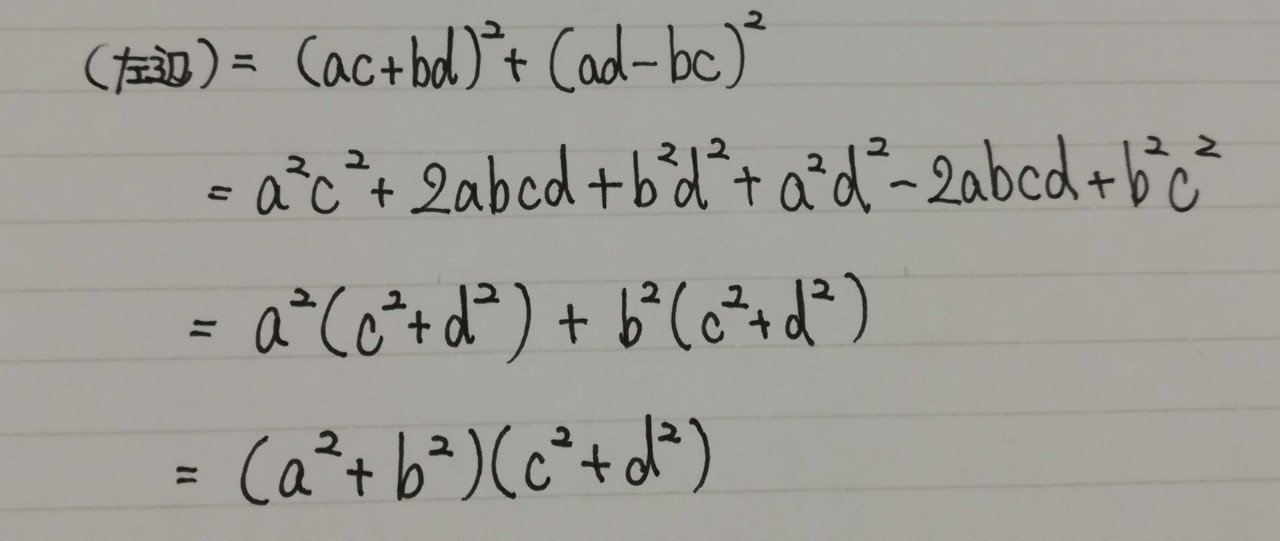
こんな感じ。
数学的な意味としては
平方数の和で表される2数の積は、やはり平方数の和で表される
で⁉️って感じはしますが入試でちょこちょこ出題されているかな。
有名な応用例は複素数の絶対値かなぁ。
卵が先か鶏が先かよくわからんが思い付いたのを書き出すと

複素数で現れるのが以外かな
(1)はここまでとしといて、(2)へ
ad-bcは簡単
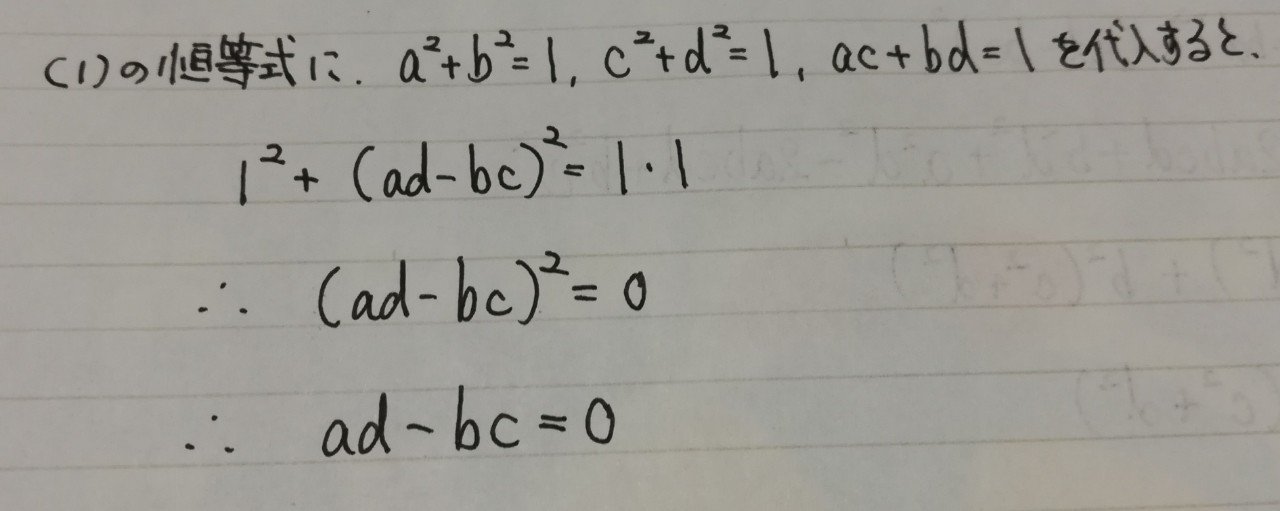
問題なのは、ここから
aとcをどうやって入れ換えるのかがポイント
そこで出てくるのが、いま求めたad-bc
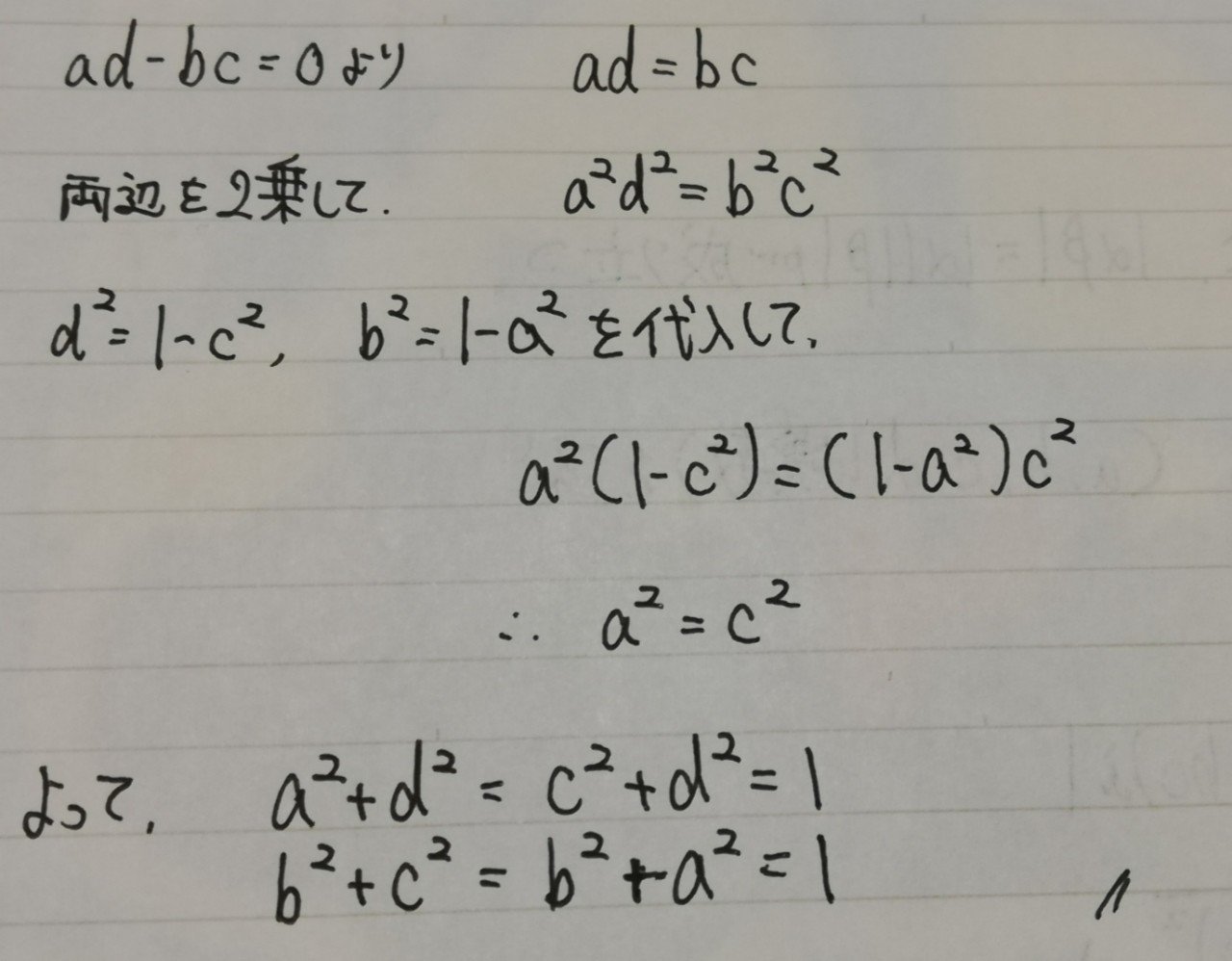
なかなか上手い解答ですなぁ~(答えの目星がついてたらナチュラルな解答なのかな⁉️)
さすらい流の解答ものしておきます。
ベタな解答ですが(高校生は中々できるようにならない…)媒介変数表示で押していきます。
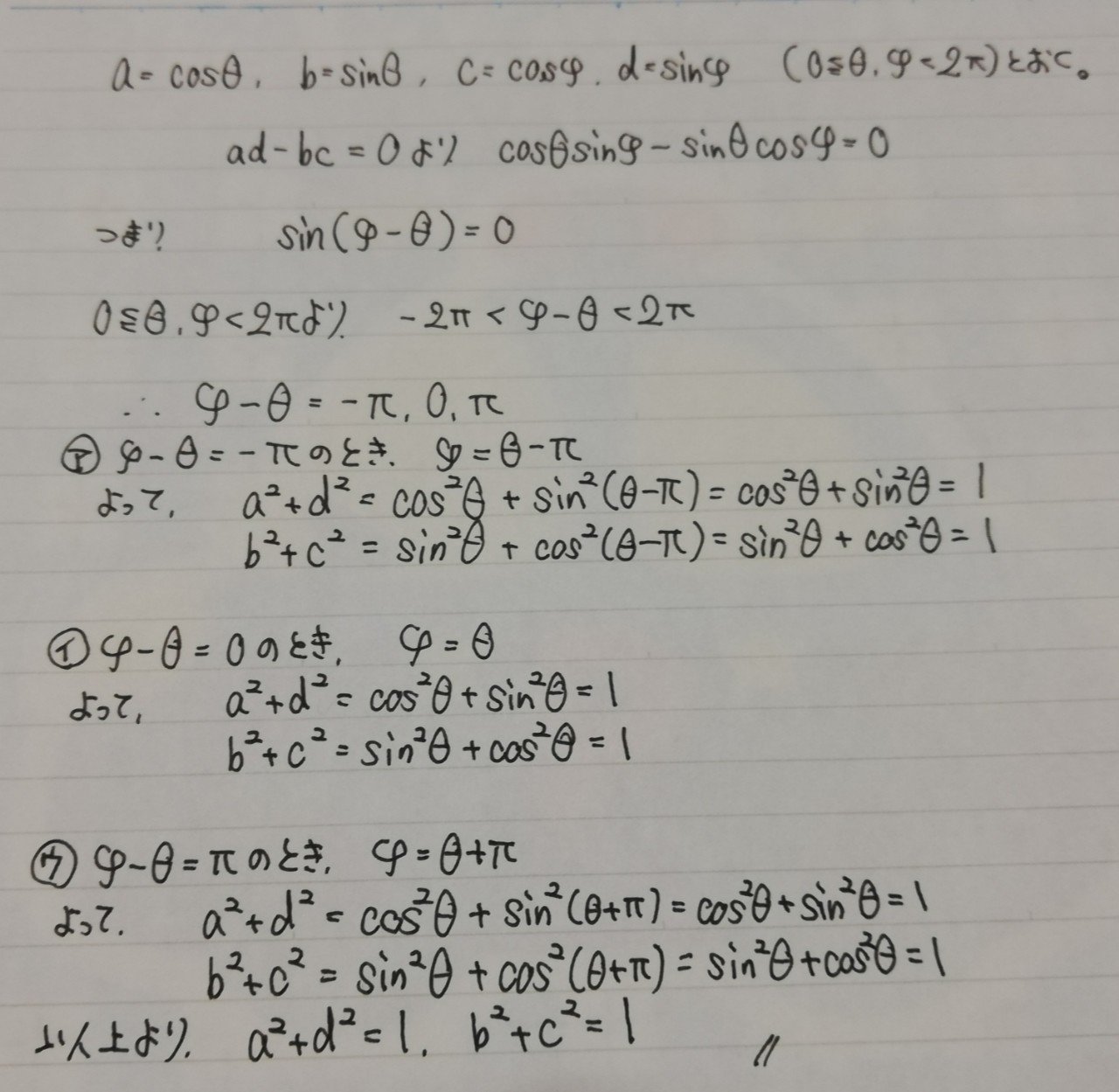
場合分けが3通り出てくるのが上の解答と比べていまいちやなぁ…まだまだ延びる余地があると思って精進します。
今週はここまで。
来週の問題はこちら

良ければ👍、フォローをお願いします。
