数学力向上のヒント#4
明日は国公立大学の入試ですね。
受験生の皆さん、今まで学んできたことをしっかり発揮して、合格をつかみとってください‼️
では、早速行ってみましょう‼️
数学力向上のヒント
敢えて、数学的帰納法を使ってみる
前回のヒントと矛盾したことを言っているような気が……
そんなことは気にせず早速、問題を紹介していきます。

いわゆる、二項定理ですね。
教科書では数学的帰納法を学ぶ前に、組み合わせ論を用いて、証明しています。ただ、n乗に関する定理なので数学的帰納法による、証明もできるようになっておくべきかと思います。
では、証明に入っていきます。
まずは、n=1のとき
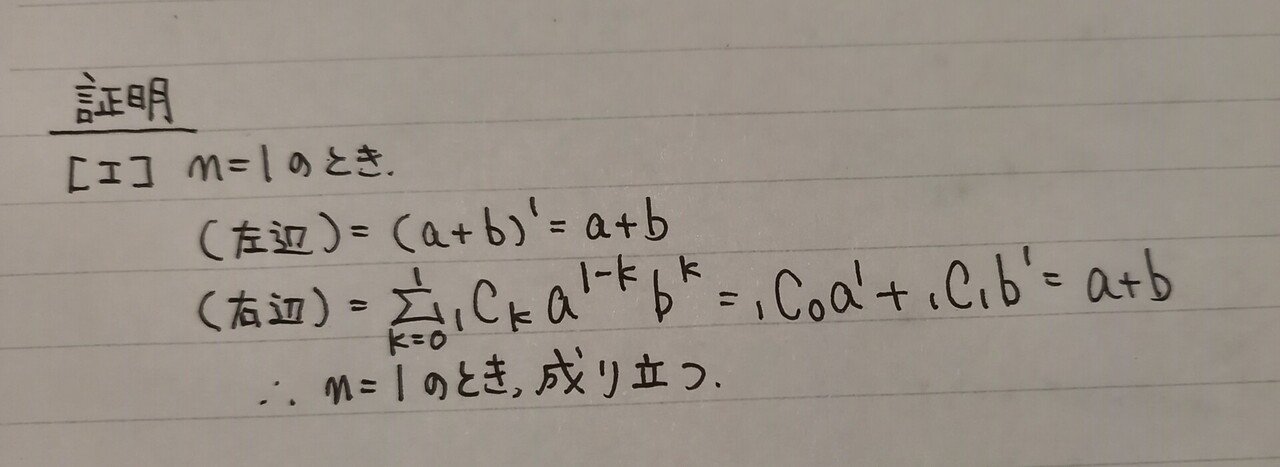
これは、あっさり解決してしまいます。
では、帰納法の本丸、仮定からの証明に入っていきます。
まずは、仮定から
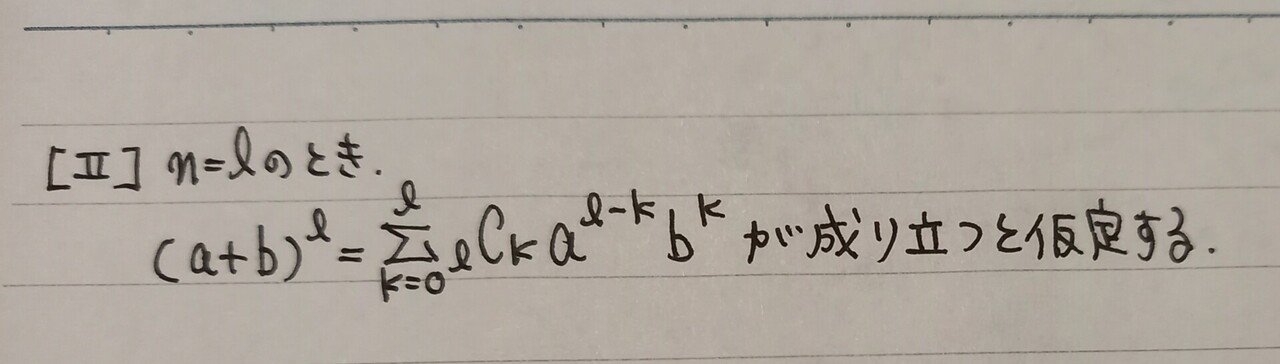
これは、簡単。
では、n=l+1の証明に入るとこのようになります。
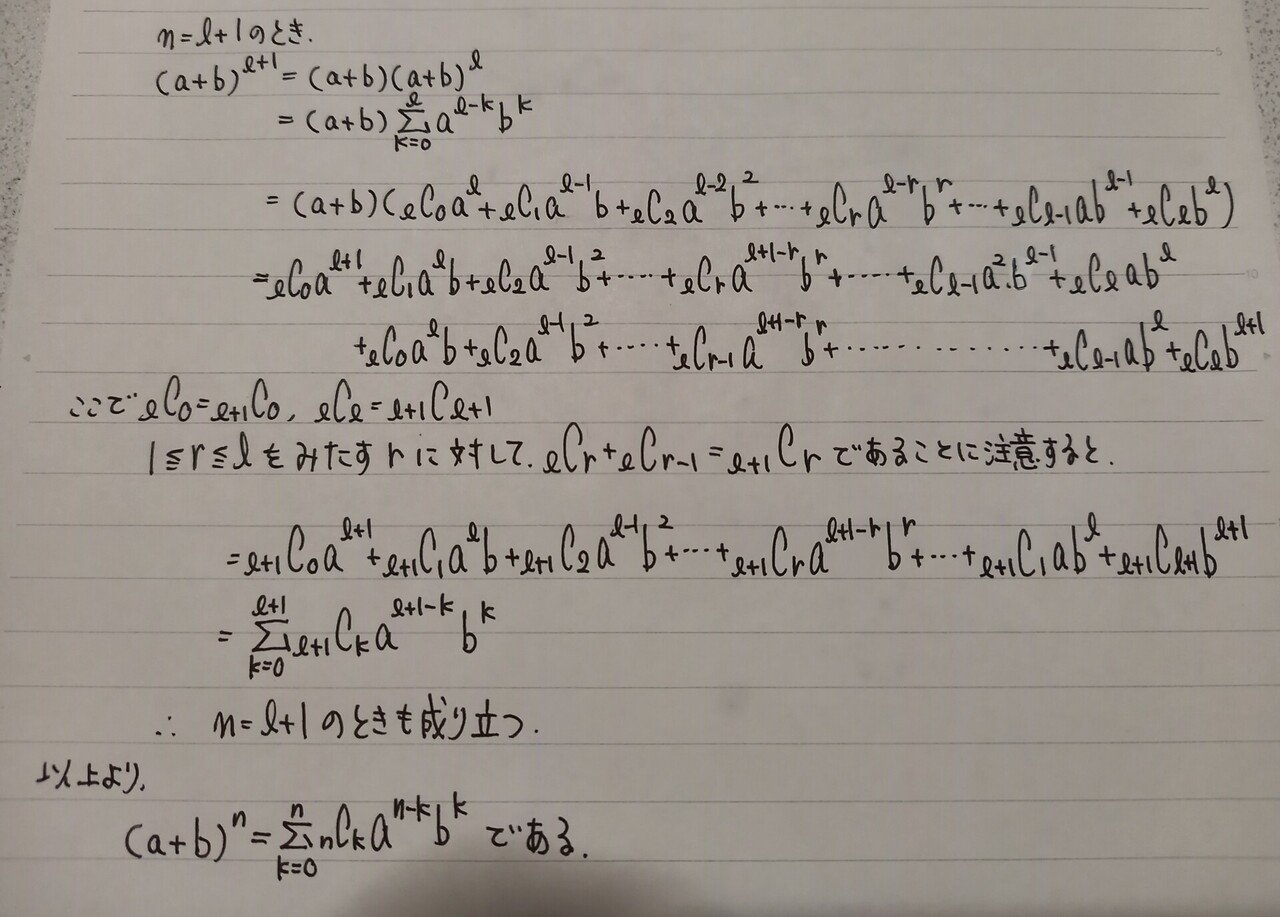
素直に展開して、数学Aで学ぶCに関しての公式を使うと証明完了となります。
Cについての公式を思い出せるのが二項定理の帰納法による証明の良いところです‼️
帰納法は記述する量が多くなることが多々あり、避けたくなりますが、帰納法を使うことで本質を浮き彫りにできることがあるので、たまには使ってあげましょう(笑)
では、今回はここまで‼️また、次回お会いしましょう‼️
この記事が気に入ったらサポートをしてみませんか?
