大学入試数学今週の一題#2

少し更新が遅くなりました(。´Д⊂)

まずは前回の出題の振り返りから

まずは(1)から

整数に関する方程式へのアプローチは

１,積の形に直す

それができなくて、現れる文字に対称性があるなら、

２、大小関係を設定し、文字の範囲を絞る

のが有効です。

本問では左辺が一次式、右辺が三次式となるので、積の形に直すのは難しい、かつ、x,y,zに対称性があるので、大小関係を設定します。

ただ、最近は大小関係が設定されている問題が多く、本問もそのようになっています。

この大小関係を定めてから数の範囲を絞るのは、
訓練が必要です。食わず嫌いせずに自分の手を動かしましょう～

するとx.yの組み合わせを考えると(x.y)=(1,1),(1,2),(1,3)の3パターン。あとは、個別にzを求めにかかります。

もしも、x,y,zの大小関係を設定した場合はx,y,zの組は1.2.3の並べ替え分、つまり3!=6通りあることを忘れないようにしましょう。

続いて(2)に進みます。

第１感としては和と積を結びつけることを考えたい‼️

そこで、和と積を結びつけるものを考えると、相加平均・相乗平均の不等式が出てきます。

実際に使ってみると鮮やかに解決します。

実は、次のような方法もあります。

そうです。有名な3次の因数分解の公式を使います。

なかなか難しいかもですが、ぜひ解けるようになってほしいです。

そしたら、今週の一題をのせて終わりにしましょう。

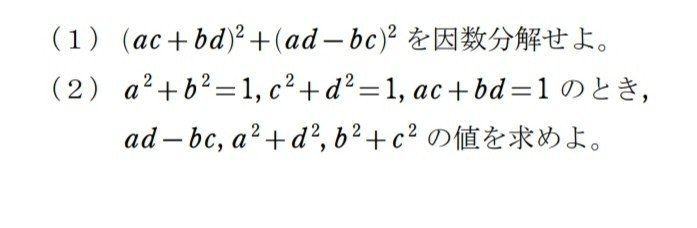
では、また来週。良ければ👍、フォローをお願いします。

#さすらいの数学者

#数学しよう

#大学入試

#高校数学

#勉強

#コロナに負けるな