
ポアソン分布
Poisson distribution(ポアソン分布)は、フランスの数学者Siméon Denis Poisson (1781 – 1840)が発表した「ランダムに発生する現象がある時間の間に何回起きるかを調べる際に用いられる確率の分布」で、ごくまれにしか起こらないような現象を大量に観測した結果が従うモデルになることが多いものです。 Frank A Haight著、”Handbook of the Poisson Distribution”, Wiley (1967) によれば、ポアソン分布とは、”a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and independently of the time since the last event.” のように説明されています。
言葉だけだと難しそうですが、例えば、新型コロナウィルスに感染する確率、きっとポアソン分布です。同じ売り場で宝くじを当てたりする確率もたぶんそうじゃないかな。他にもたくさんの事例があります。有名なものとしては、ロシアの経済学者 Ladislaus Josephovich Bortkiewicz (1868 – 1931)は、著書"Das Gesetz der kleinen Zahlen "(The Law of Small Numbers)のなかで、プロイセン陸軍の14の騎兵連隊の中で、1875年から1894年にかけての20年間で馬に蹴られて死亡する兵士の数がポアソン分布に従うことを示しました。
ポアソン分布は、「与えられた時間内に平均で λ 回発生する事象がちょうど k 回(k は自然数)発生する確率」として
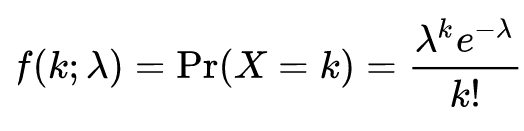
のようにあらわせます。
さて、そのポアソン分布ですが、当研究室で行っているX線スペクトルやX線イメージングの研究でも大いに関わりがあります。微弱な信号を扱うとき、あるいは、そのような条件下での雑音の影響など、ポアソン分布を考慮する必要があります。十分なカウント数が得られる時は、よく知られているガウス分布に移行するのですが、そうでないときは、注意が必要です。ところが、案外、いろいろなデータ処理を見ると、ポアソン分布を考慮せずに行われるていると思われることが多いのです。
そこで、2020年に入って、当研究室の大学院生たちは、毎週の輪講で、この問題を議論しています。テキストは、Mario Bertero, Patrizia Boccacci and Valeria Ruggiero著、"Inverse Imaging with Poisson Data: From cells to galaxies" (IOP Expanding Physics) です。
当研究室は、自分たちの専門に近いところでポアソン分布とつきあっていますが、その立場を離れ、もっと他の側面にも注目すると、面白い話がいっぱいあります。またそんなことも書いてみたいです。
※ この記事は、まったく存じ上げない不特定多数の方々にお伝えすることを意図していません。そのため、少し敷居を高くし、将来は有料とさせて頂くことを検討しています。まだ、note は始めたばかりなので、当面は、何も設定いたしておりません。
※ なお、マガジン「群盲評象」には、この記事を含めた私的ノート(有料のものも含む)を収録いたしております。ご関心のある方は、ぜひお求めください
ここから先は

群盲評象2020(580過去記事、2021年7月末まで)
本マガジンは、2019年12月29日から2021年7月31日までのおよそ580日分、元国立機関の研究者、元国立大学大学院教授の桜井健次が毎…
いつもお読みくださり、ありがとうございます。もし私の記事にご興味をお持ちいただけるようでしたら、ぜひマガジンをご検討いただけないでしょうか。毎日書いております。見本は「群盲評象ショーケース(無料)」をご覧になってください。
