
31.02 ベクトルの初歩(ベクトルの和・差)
前回はベクトルを導入し、その後、逆ベクトル、零ベクトル、実数倍されたベクトルを紹介しました。今回はベクトルに "和" と呼ばれるものを定義し、それから派生することについて話をします。
質問 幾何ベクトル (ベクトル) とは何でしたか。
こういう場合は定義を述べるものですが、その述べ方は一字一句教科書通りでなくても構いません。自分自身がどう理解しているかが大切なのです。
ポイントとなるのは、これまでの量とは異なり、2つの量を持っていたことです。その2つの量とは、向きと長さ (大きさ) でした。この2つの量が等しいものをまとめて1つのものとして考えたのがベクトルです。
幾何ベクトルと呼ばれるのは有向線分を用いて幾何的に定義したからです。そのベクトルに "和" というものを定義するのに、次のように捉え直します:ベクトルはある点から点への移動を与えている。つまり、向きは移動する方向で、長さは移動する距離を表しているとみます。
ベクトルの和(ベクトルの足し算)
2つのベクトル$${\vec{a}}$$と$${\vec{b}}$$の和を形式的に$${\vec{a}+\vec{b}}$$と書くことにし、$${\vec{a}}$$による点の移動後に続いて$${\vec{b}}$$による点の移動を行うことを意味するとします。図で示すと次のようになります。
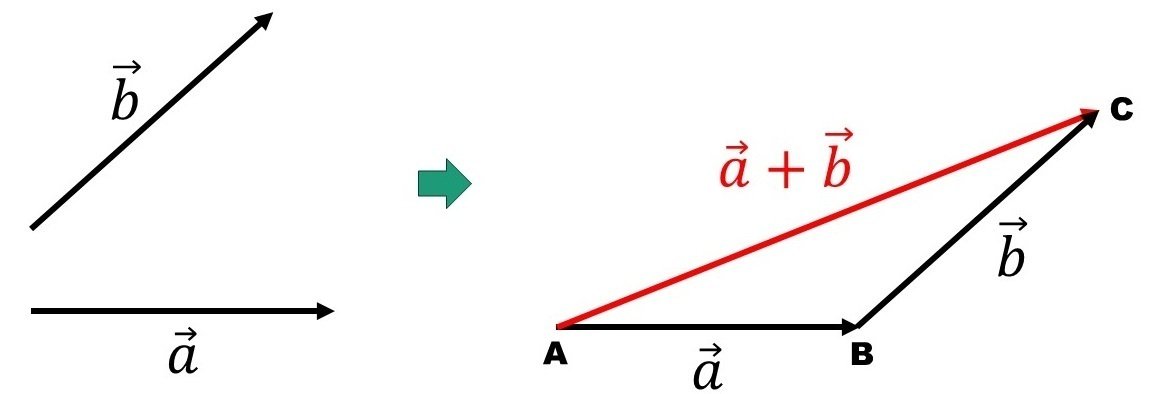
平行移動させて、$${\vec{a}}$$の終点と$${\vec{b}}$$の始点を一致させると2つのベクトルの和が得られます。上右図の点Bが結合部分に当たり、その結果として点Aを始点、点Cを終点とするベクトルが得られます。これが2つのベクトルの和$${\vec{a}+\vec{b}}$$となります。
注:上図の$${\overrightarrow{\mathrm{AB}}}$$は$${\vec{a}}$$の一つです。同様に、$${\overrightarrow{\mathrm{BC}}}$$も$${\vec{b}}$$の一つです。他にもたくさん考えられます。下図はその一例です。

$${\vec{a}=\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{DE}}}$$, $${\vec{b}=\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{EF}}}$$とすると、$${\vec{a}+\vec{b}=\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{DF}}}$$です。
なぜなら
$${\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{DE}}}$$なので AB//DE かつ AB=DE より 四角形ABEDが平行四辺形となります。四角形BCFEも同様です。これにより四角形ACFDが平行四辺形になるからです。
点Dは任意にとっても構わないので、これにより平行移動を除いて、2つのベクトルの和が一意的に決まることが分かりました。最初は、この大切さに気づけないと思いますが構いません。このことによって安心してベクトルの和が考えられるのです(※1)。
注2:ベクトルの和によって、2つのベクトルから新たなベクトルが得られます。これによって、ベクトルの和にベクトルを足すことができます:
$${(\vec{a}+\vec{b})+\vec{c}}$$
を考えることができます。
前回は実数倍されたベクトルを紹介しましたが、それはベクトルを実数倍することによって新たなベクトルが得られるというものでした。
"和"と呼ばれる所以
数の和に関してどのような性質が成り立つか覚えていますか。これに答えられるようなら数学しています。高校数学の段階では答えられる方が稀です。
数$${a, b, c}$$に対して次が成り立ちました。
$${(a+b)+c=a+(b+c)}$$ (結合律)
$${a+b=b+a}$$ (交換律)
こういうのは大学以降の数学をするとだんだん覚えられます。計算よりも成り立ちに関心が向くからです。高校までの数学はそういうことをほとんどしないので覚えられないのは当然なのです。だから無理に覚える必要はありません。
さて、ベクトルの和に関しても結合律と交換律が成り立ちます。つまり
$${(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})}$$ (結合律)
$${\vec{a}+\vec{b}=\vec{b}+\vec{a}}$$ (交換律)
が成り立ちます。これが "和" と呼ばれる所以です。
次の図は、結合律および交換律が成り立つ理由を表しています。

左図において、$${\vec{a}+\vec{b}}$$と$${\vec{c}}$$を足すと赤い矢印になり、$${\vec{a}}$$と$${\vec{b}+\vec{c}}$$を足しても赤い矢印になります。
右図は平行四辺形で、赤い矢印はその対角線です。
注3:結合律が成り立つので、括弧を省略することができます。
例1 直方体ABCD-EFGHにおいて、$${\vec{a}=\overrightarrow{\mathrm{AB}}, \: \vec{b}=\overrightarrow{\mathrm{AD}}, \: \vec{c}=\overrightarrow{\mathrm{AE}}}$$とするとき、$${\vec{a}+\vec{b}+\vec{c}}$$が表すベクトルを考えてみます。

$${\vec{a}+\vec{b}+\vec{c}}$$
=$${\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{AE}}}$$
=$${(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}})+\overrightarrow{\mathrm{CG}}}$$
=$${\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{CG}}}$$
=$${\overrightarrow{\mathrm{AG}}.}$$ ▮
注4:$${\vec{a}+\vec{b}+\vec{c}=\vec{0}}$$となることがありますが、どのような場合か見当がつきますか。
三角形ABCを考えてください。このとき
$${\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CA}}=\vec{0}}$$
が成り立ちます。左辺は結果的にAからAへの移動なので、$${\overrightarrow{\mathrm{AA}}}$$ですが、これが$${\vec{0}}$$です。前回紹介した零ベクトルは和を考えると、このように必然的に現れるのです。
ベクトルの差(ベクトルの引き算)
代数を意識して説明します。
2つのベクトル$${\vec{a}, \vec{b}}$$に対して
$${\vec{a}+\vec{x}=\vec{b}}$$
を満たすベクトル$${\vec{x}}$$が唯一つ存在し、それを$${\vec{b}-\vec{a}}$$と書くことにします。
特に、$${\vec{b}=\vec{0}}$$のとき
$${\vec{a}+\vec{x}=\vec{0}}$$
を満たす$${\vec{x}}$$は前回紹介した$${\vec{a}}$$の逆ベクトル$${-\vec{a}}$$です。$${\vec{0}-\vec{a}}$$を$${-\vec{a}}$$と書くと約束したとみることができます。逆ベクトルを表すのにマイナスを用いた理由はここにあります。
$${\vec{a}+\vec{x}=\vec{b}}$$を図で考えてみましょう:

図から
$${\vec{x}=(-\vec{a})+\vec{b}=\vec{b}+(-\vec{a})}$$
であることが分かります。つまり、差$${\vec{b}-\vec{a}}$$は
$${\vec{b}-\vec{a}:=\vec{b}+(-\vec{a})}$$
と定義されます。これより
$${\vec{a}-\vec{a}=\vec{a}+(-\vec{a})=\vec{0}}$$
となります。
和と差のポイント
長くなってしまったので、最初の段階で覚えておいてほしいことをまとめておきます。
和について:幾何ベクトルでは点の移動の結果とみる。
$${\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{AC}}.}$$
差について:逆ベクトルを利用して捉えることができる。
$${\vec{b}-\vec{a}:=\vec{b}+(-\vec{a}).}$$
具体例で確認しましょう。
例2 平行四辺形ABCDにおいて、$${\vec{a}=\overrightarrow{\mathrm{AB}}, \: \vec{b}=\overrightarrow{\mathrm{AD}}}$$とするとき、$${\vec{a}-\vec{b}}$$が表すベクトルを考えてみます。

$${\vec{a}-\vec{b}}$$
$${=\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{AD}}}$$
$${=\overrightarrow{\mathrm{AB}}+(-\overrightarrow{\mathrm{AD}})}$$
$${=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{DA}}}$$
$${=\overrightarrow{\mathrm{DA}}+\overrightarrow{\mathrm{AB}}}$$
$${=\overrightarrow{\mathrm{DB}}.}$$ ▮
注意:説明のためにこう書きましたが、図を使って考えれば結論がかんたんに得られると思います。$${\vec{b}}$$の逆ベクトルを図で考えてみてください。
例3 直方体ABCD-EFGHにおいて、$${\vec{a}=\overrightarrow{\mathrm{AB}}, \: \vec{b}=\overrightarrow{\mathrm{AD}}, \: \vec{c}=\overrightarrow{\mathrm{AE}}}$$とするとき、$${\vec{a}-\vec{b}-\vec{c}}$$が表すベクトルを考えてみます。

$${\vec{a}-\vec{b}-\vec{c}}$$
=$${\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{AD}}-\overrightarrow{\mathrm{AE}}}$$
=$${(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{DA}})+\overrightarrow{\mathrm{EA}}}$$
=$${(\overrightarrow{\mathrm{DA}}+\overrightarrow{\mathrm{AB}})+\overrightarrow{\mathrm{EA}}}$$
=$${\overrightarrow{\mathrm{DB}}+\overrightarrow{\mathrm{EA}}}$$
=$${\overrightarrow{\mathrm{HF}}+\overrightarrow{\mathrm{FB}}}$$
=$${\overrightarrow{\mathrm{HB}}.}$$ ▮
注意:上と同様、図を使って考えれば結論がかんたんに得られると思います。図で、$${\vec{a}+(-\vec{b})+(-\vec{c})}$$を考えてみてください。
安心して創作活動が続けられるよう応援してくださると助かります。いただいたチップは書籍もしくは文具の購入に当てたいと思います。

