32.07 ２次曲線（極方程式）

平面上において直交座標$${(x, y)}$$に関するいろいろな方程式を扱ったように、極座標に関する方程式を扱います。例えば、方程式$${r=\theta}$$などです。
この方程式はどのような図形を描くと思いますか。答えは後ほど。

極方程式

本題に入る前に

質問　極座標を、具体例を挙げて説明してください。

答えられましたか。例えば

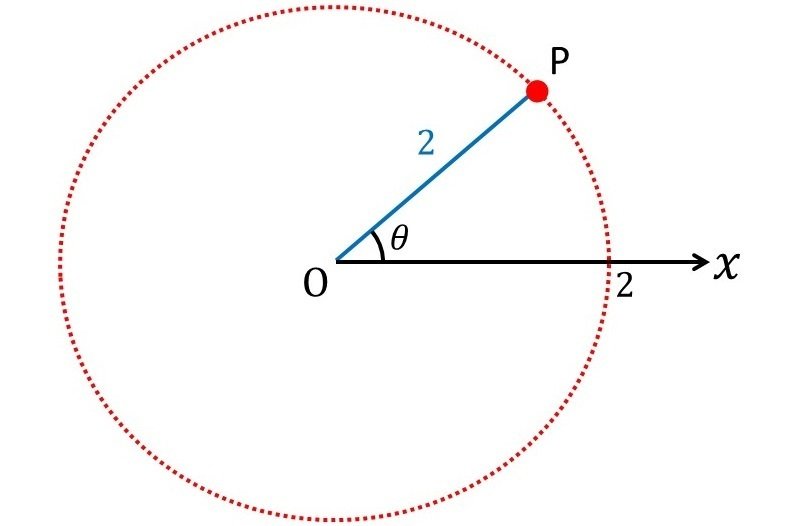
極座標が$${(2, \: \dfrac{\:\pi\:}{6})}$$は、極からの距離が２で、偏角が$${\dfrac{\:\pi\:}{6}}$$の点を表しています。偏角というのは、始線を基準にした角の大きさを表しています。
※ 図を書きながら説明できれば十分です。

極方程式

平面上の曲線は、直交座標$${(x, y)}$$を用いて

$${y=f(x)}$$　または　$${F(x,y)=0}$$

などのような形で表しました。今回紹介する極方程式というのは、極座標$${(r,\theta)}$$を用いて

$${r=f(\theta)}$$　または　$${F(r,\theta)=0}$$

のように表される方程式をいいます。冒頭で挙げた方程式$${r=\theta}$$は前者に当たり、これを

$${r-\theta=0}$$

と書けば後者になります。

極方程式の具体例

例１　極方程式$${r=2}$$の表す図形という場合、この方程式を満たす点全体のことをいいます。つまりその図形$${\text{F}}$$というのは

$${\text{F}=\{(r, \theta)\mid r=2 \quad (r, \theta\in \mathbb{R})\}}$$

のことです。ではどのような点の集まりかというと

極座標$${(2, \theta)}$$全体です。ただし、$${\theta}$$は任意の実数。

これを図示すると次のようになります：

これは極Ｏを中心とする半径２の円です。
逆に、このような円は方程式$${r=2}$$で表すことができます。

もしも極Ｏを中心とする半径５の円を極方程式で表したいなら

$${r=5}$$

となります。
では点$${(1, 0)}$$を中心とする半径１の円は･･･平行移動だからといって、直交座標のときとは違い、かんたんに表すことができません。この答えは例３をご覧ください。

例２　極座標で表された点Ａ$${(1, 0)}$$を通り、始線に垂直な直線の極方程式を求めてみます。

直線上の任意の点Ｐの極座標を$${(r, \theta)}$$とし、$${r, \: \theta}$$に関する関係式を見つけ出します。

直角三角形OAPに着目すると

$${r\cos\theta=1}$$

を得ます。これが求める極方程式です。
さて、ここで$${\theta}$$の取る得る範囲が気になりませんか。角の大きさだけに着目すれば

$${-\dfrac{\:\pi\:}{2}< \theta < \dfrac{\:\pi\:}{2}}$$

ということに気づくと思います。これをさらに一般化して

$${\theta\neq \dfrac{\:\pi\:}{2}+n\pi\:\:(n\in\mathbb{Z})}$$なる実数

とすることができます。でも$${\theta=\dfrac{\:2\pi\:}{3}}$$のときは

$${r\cos\dfrac{\:2\pi\:}{3}=1,}$$

$${r=-\dfrac{\:1\:}{2}}$$

となります。$${r}$$は$${r\geqq 0}$$で考えていたのでおかしなことが起こっていますが、次のように約束することで解決します。

約束　$${r< 0}$$の場合は　$${(r, \theta)}$$　を　$${(|r|, \pi+\theta)}$$　と考える

例えば、３点$${(-\dfrac{\:1\:}{2}, \dfrac{\:2\pi\:}{3}), \: (\dfrac{\:1\:}{2}, \dfrac{\:5\pi\:}{3}), \: (\dfrac{\:1\:}{2}, -\dfrac{\:\pi\:}{3})}$$は同じ点です。

こうすると$${r}$$も$${\theta}$$も実数全体で考えることができて、極方程式が扱いやすくなります。

例３　極方程式$${r=2\cos\theta}$$は円を表します。下図において

$${r, \: \theta}$$は極方程式$${r=2\cos\theta}$$を満たしています。このときの点Ｐは２直線OP, APが直交しているときの交点です。このような点の軌跡は、円に関する平面図形の性質から

OAを直径とする円

であることが分かります。いわゆる「円周角の定理の逆」です。
例６で円となる理由がよく分かると思います。▮

※ 例１の最後に触れましたが、直交座標のときとは違い、平行移動したときの図形の方程式がかんたんに表せないことが分かりました。

３つの例から分かるように、極方程式を必ずしも

$${r=f(\theta)}$$　または　$${F(r,\theta)=0}$$

の形で表す必要はありません。
理解を深めるために次の問題を考えてみてください。

練習問題１

次の図形を表す極方程式を求めよ．
(1)  極座標$${(2, \dfrac{\:\pi\:}{2})}$$の点を通り，始線に平行な直線

(2)  極Ｏを通り，始線との成す角が$${\dfrac{\:\pi\:}{6}}$$の直線

(3)  極座標$${(3, 0)}$$を中心とする半径３の円