
忙しい人のための中学数学【正負の数(計算ルール編)】
〜今回のテーマ〜
正負の数の計算について、ルールを覚えよう。
はじめに
このシリーズでは、各教科・各単元に登場する基本事項(用語やその定義、公式等)を中心にまとめていきます。
現役中学生・高校生の軽い予習・復習、テスト勉強の最終確認はもちろん、「社会人枠で受験することになったから入試対策をしたい」、「子どもの勉強をサポートしてあげたい」等といった大人の皆さんもよろしければご活用ください。
どの単元の学習でも基本を理解し、問題の中で使いこなせるようになることは、とても大切なことです。ある単元で学習したことが、別の単元で活かされることもたくさんあります。1つ1つ積み上げていきながら、土台を固めながら学習を進めていきましょう!
※できるだけ「わかりやすく」を目指していますが、今回のシリーズはあくまでも「忙しい人のための」シリーズなので、細かい部分まではまとめきれないこともあります。「もっと掘り下げて学習したい!」という人は、各自教科書や参考書、問題集等を活用しましょう。
文字ばかりで難しく感じるなぁという人は、声に出して読んでみることをオススメします!
その他の単元や計算問題はこちら
↓ ↓ ↓
2数の加法
○正負の数の加法の考え方
まずは、数直線を使った考え方を紹介します。
第1問 (+2)+(+3)
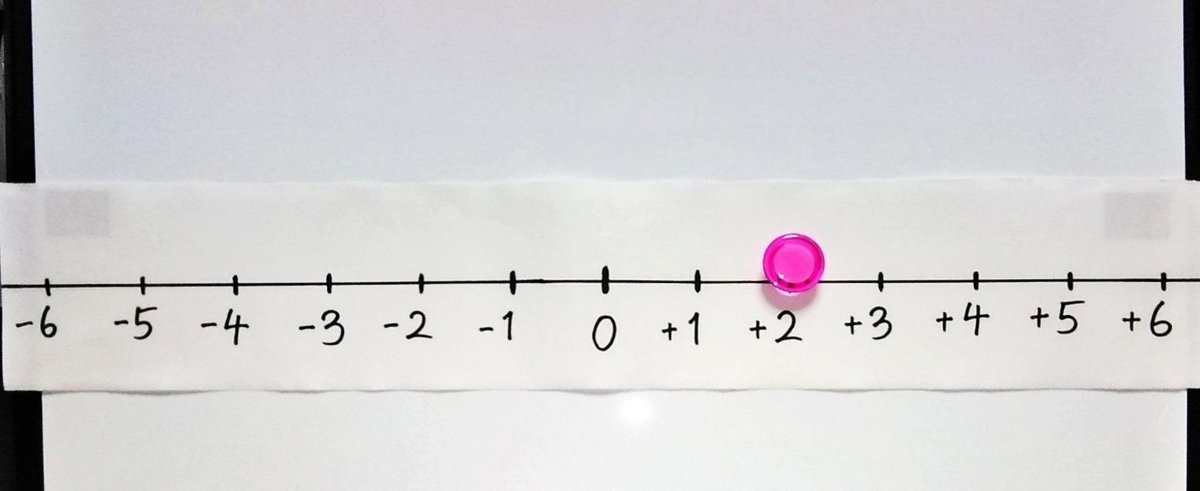
最初の問題です。数直線の(+2)からスタートします。

「(+3)をたす」ということは、スタートの(+2)から正の方向(+側、右側)に3進むということです。止まったところは+5……つまり、この問題の答えは+5です。
※別パターンの書き方↓

0からスタートして考えると、このようになります。
第2問 (−2)+(−3)

次の問題は、数直線の(−2)からスタートします。

「(−3)をたす」ので、今度はスタートの(−2)から負の方向(−側、左側)に3進むことになります。止まったところは−5ですね。これがこの問題の答えです。
※別パターンの書き方↓

0からスタートすると、このようになります。
(わかりやすいように負の方向に進む矢印を青色にしてみました。)
正負の数の加法では、正の数をたすときは数直線上を正の方向(右側)に進め、負の数をたすときは数直線上を負の方向(左側)に進める、ということになります。
第3問 (+5)+(−7)

この問題では、(+5)がスタート地点ですね。

「(−7)をたす」ので、負の方向に7動かします。そうすると、−2で止まりますね。この問題の答えは−2ということになります。
※別パターンの書き方↓

まず0からスタートして正の方向に5進み、次に負の方向に7進みます。止まったところがこの問題の答えです。「矢印で表したところは、何メモリ分はみ出している?差はどのくらいある?」と考えても良いですね。
(わかりやすいように正の方向に進む矢印を赤色、負の方向に進む矢印を青色にしてみました。)
第4問 (−4)+(+8)

最後の問題です。スタートは(−4)です。

「(+8)をたす」ので、正の方向に8動かすと……+4で止まります。この問題の答えは+4ということになります。
※別パターンの書き方↓

まず0からスタートして負の方向に4進み、次に正の方向に8進みます。止まったところがこの問題の答えです。こちらも「矢印で表したところは、何メモリ分はみ出している?差はどのくらいある?」と考えても良いですね。
(わかりやすいように正の方向に進む矢印を赤色、負の方向に進む矢印を青色にしてみました。)
「+と−をたすってどういうこと?」、「−と−をたすってどういうこと???」とごちゃごちゃしてしまったときは、この数直線を使った考えを思い出してみましょう。
しかし、「いちいち数直線書くのもめんどくさいよ!」、「大きい数の計算になったら大変だよ!」ということにもなってきますよね。そこで、次は数直線を使わずに、式を書いて答えを出していくやり方を紹介します。学校の教科書等でも紹介されているやり方になりますが、「計算のルール・手順」として確認してみましょう。
このとき、先程紹介した数直線のやり方での●の動かし方(●を動かす方向)も思い浮かべてみると良いかも……。
○同符号の2数の和は、そのまま絶対値(+や−のすぐ後ろの数字の部分)を足せば大丈夫です。符号もそのまま共通の符号を付けます。
(例題)正の数+正の数
(+5)+(+3)
=+8
→絶対値、つまり数字の部分をそのままたし算して良いので「5+3」、符号もそのまま共通で良いので「+」を付けます。
(例題)負の数+負の数
(−7)+(−2)
=−9
→こちらも絶対値をそのままたし算して良いので「7+2」、符号もそのまま共通で良いので「−」を付けます。
○異符号の2数の和は、絶対値が大きいほうから小さいほうをひきます。符号は絶対値が大きいほうの符号を付けます。
(例題)
(+6)+(−4)
=+(6−4)
=+2
→絶対値が大きいのは「6」なので「6−4」、符号は絶対値が大きいほうの符号を付けるので「+」になります。
(例題)
(+5)+(−9)
=−(9−5)
=−4
→絶対値が大きいのは「9」なので「9−5」、符号は絶対値が大きいほうの符号を付けるので「−」になります。
○絶対値が等しい異符号の2数の和は、0になります。
(例題)
(+8)+(−8)
=0
(−3)+(+3)
=0
○どんな数に0をたしても、和はその数のままです。また、0にどんな数をたしても、和はたした数になります。
(例題)
(+6)+0
=+6
(−10)+0
=−10
0+(+3)
=+3
0+(−8)
=−8
○小数・分数であっても計算の進め方は同じです。
○たされる数とたす数を入れても、和は変わりません。
2+3
も
3+2
も、どちらも5になります。この
a+b=b+a
となる法則を、加法の交換法則(かほうのこうかんほうそく)といいます。
2数の減法
減法は「符号を変えてたす」というやり方で計算します。「+7をひく」ということは「−7をたす」ということ、「−5をひく」ということは「+5をたす」ということ……といった感じ。
(例題)
(−2)−(+7)
=(−2)+(−7)
=−9
(+5)−(−5)
=(+5)+(+5)
=+10
→最初の符号を変える作業さえ終われば、あとは加法として解くだけです。
加法と減法の混じった計算
○まず、また1つ法則の紹介から……。例えば
(1+2)+3
の和も
1+(2+3)
の和も、どちらも同じ6になります。この
(a+b)+c=a+(b+c)
となる法則を加法の結合法則(かほうのけつごうほうそく)といいます。
○加法と減法が混じった式の計算は、まず減法を加法に変えるところから始めます。加法だけの式にした後は、項を符号ごとに並べ替えると計算しやすいと思います。加法の交換法則の出番です。
(例題)
(+5)−(+3)+(−6)−(−8)
=(+5)+(−3)+(−6)+(+8)
=(+5)+(+8)+(−3)+(−6)
=(+13)+(−9)
=+(13−9)
=+4
並べ替えた後は、上のように同符号同士の計算を先にして、最後に異符号の2数の加法を……という手順です。
もう一度まとめると、
①減法が混じっていたら、符号を変えて加法だけの式にする。
②符号ごとにまとまるように並べ替える。
③同符号の加法をそれぞれ。
④残った異符号の2数の加法を。
という流れです。
もう1問例題を載せておきます。
(例題)
(−11)+(+2)−(−7)−(+4)
=(−11)+(+2)+(+7)+(−4)
=(+2)+(+7)+(−11)+(−4)
=(+9)+(−15)
=−(15−9)
=−6
慣れてきたら②の過程は飛ばしても良いかもしれませんが、慣れるまではできるだけ細かく途中を書いて残しながら計算していくのがオススメです。
暗算でなんとなくそれっぽい計算を……というのはミスにつながりやすいのでオススメしません!ルールを理解して、1つ1つ計算を進めていくことが大切です。
2数の乗法
○同符号の2数の乗法は、必ず符号が+になります。あとは絶対値をそのままかけるだけ!
(例題)
(+2)×(+8)
=+16
(−5)×(−4)
=+20
○異符号の2数の乗法は、必ず符号が−になります。あとは絶対値をかけるだけ!
(例題)
(+6)×(−7)
=−42
(−4)×(+8)
=−32
○ある数と1との積は、もとの数のままです。
(例題)
5×1
=5
(−7)×1
=−7
1×11
=11
1×(−9)
=−9
○「−(−●)」というのは「(−1)×(−●)」ということであり、計算すると「(+●)」になります。
(例題)
−(+4)
=(−1)×(+4)
=−4
−(−13)
=(−1)×(−13)
=+13
→「符号を変えた数になる」と考えれば大丈夫です!
○0にどんな数をかけても、積は0です。また、どんな数でも、0をかけると積は0になります。
(例題)
0×(+6)
=0
0×(−3)
=0
(+11)×0
=0
(−9)×0
=0
3数以上の乗法
○式の中にいくつ負の符号があるかによって積の符号が決まってきます。
負の符号が偶数個なら、積の符号は+
負の符号が奇数個なら、積の符号は−
(例題)
(+1)×(−2)×(−3)×(+4)
=+24
(−1)×(−2)×(+3)×(−4)
=−24
○加法に「交換法則」と「結合法則」がありましたが、この法則は乗法でも成り立ちます。
a×b=b×a
(a×b)×c=a×(b×c)
(例題)
5×6=6×5
→どちらも積は30ですね。
(3×4)×5=3×(4×5)
(3×4)×5
=12×5
=60
3×(4×5)
=3×20
=60
→どちらも積は60ですね。
2数の除法
○整数や小数の、割り切れる計算の場合はそのままわり算の計算として進めて大丈夫です。注意しなければならないのは、やっぱり符号。
正の数÷正の数=商の符号は+
負の数÷負の数=商の符号は+
正の数÷負の数=商の符号は−
負の数÷正の数=商の符号は−
(例題)
(+16)÷(+4)
=+4
(−24)÷(−4)
=+6
(+32)÷(−8)
=−4
(−10)÷(+5)
=−2
→符号の組み合わせは、繰り返し練習して正確に覚えていきましょう。
○整数で割り切れない除法や分数を含む除法は、「逆数をかける」計算の仕方で解いてみましょう。
(個人的には分数を含むか含まないか等関係なく、こちらの計算の仕方がオススメ。)
「除法を乗法に変える」という手順は、「減法を加法に変える」という手順とよく似ていますね。
(例題)
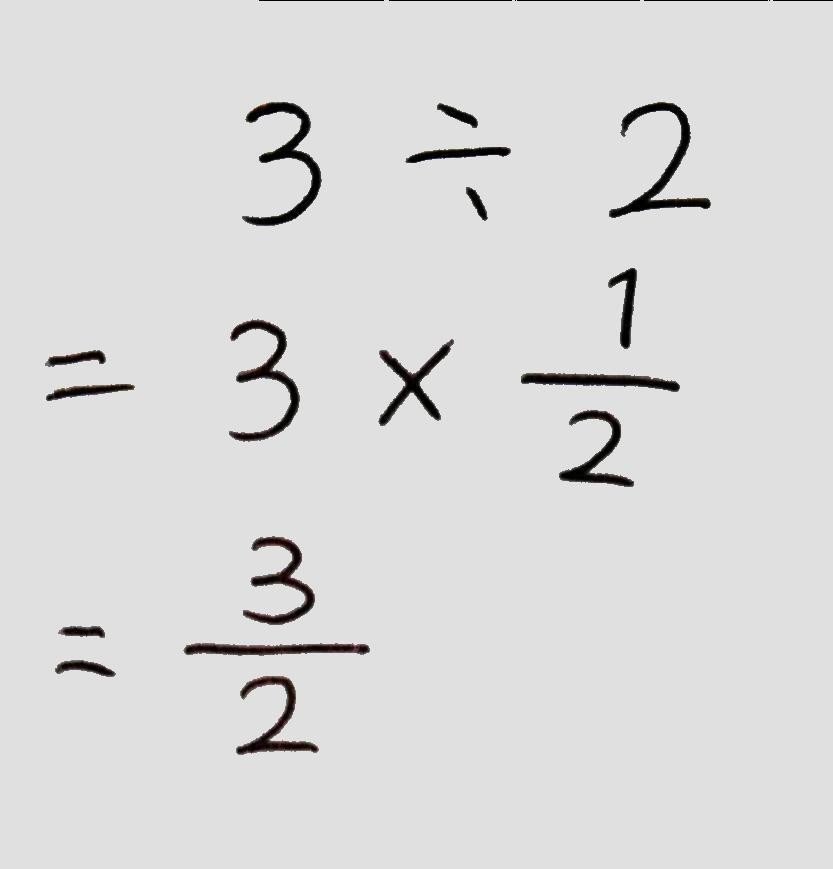
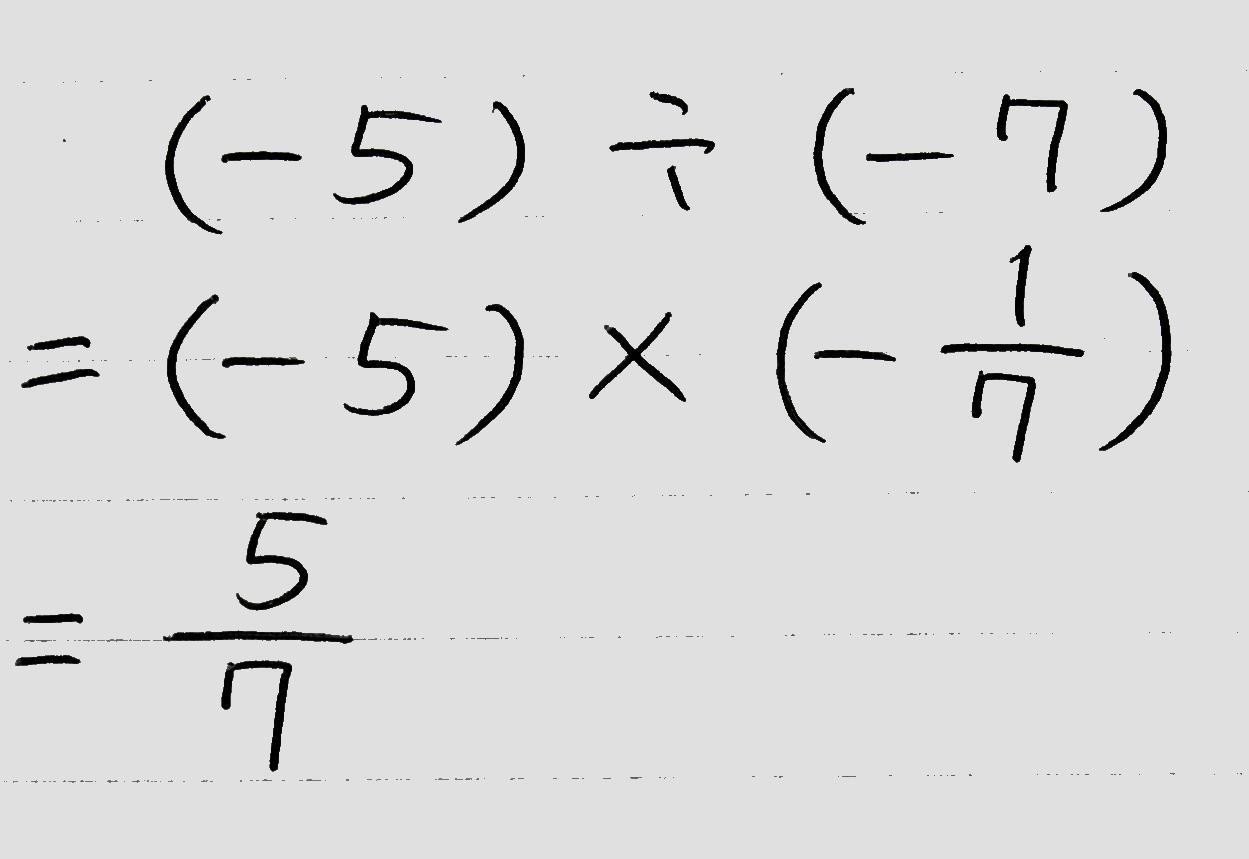
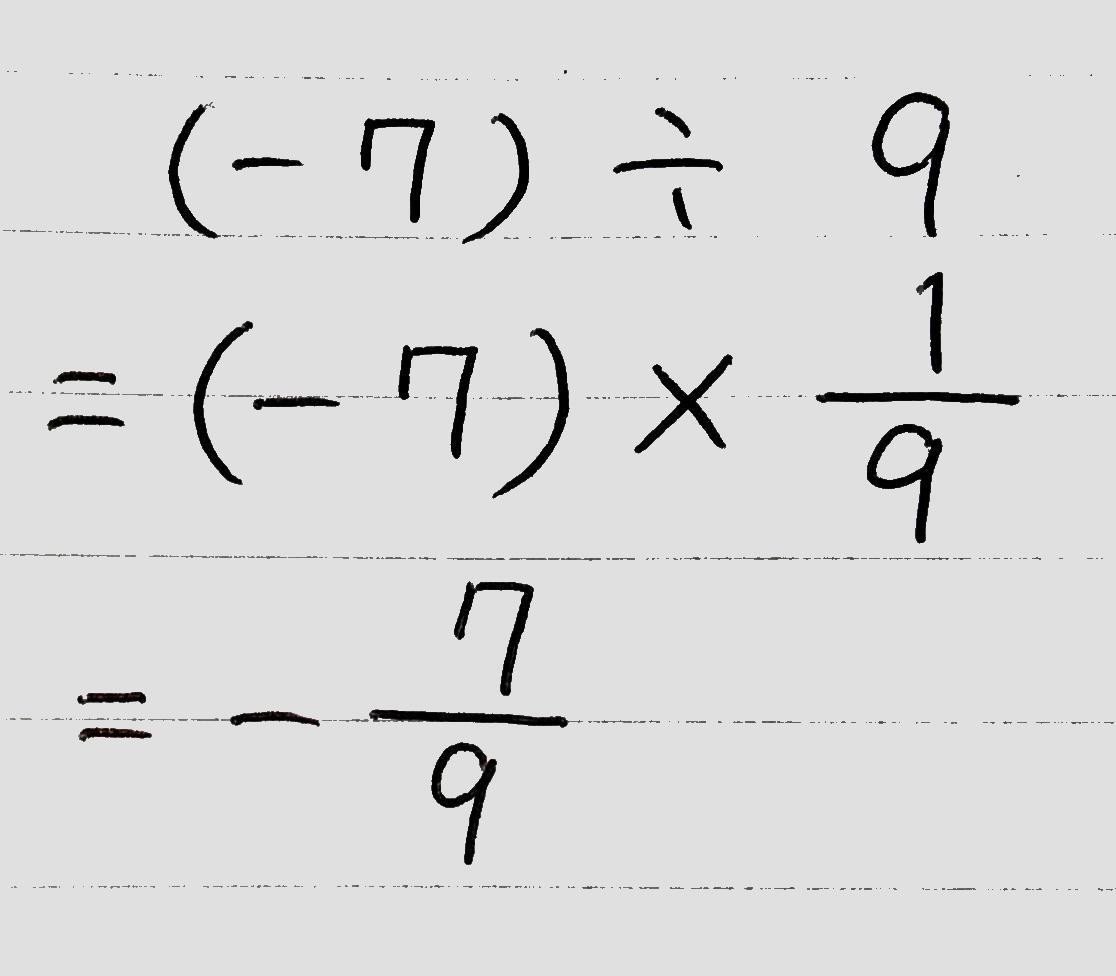
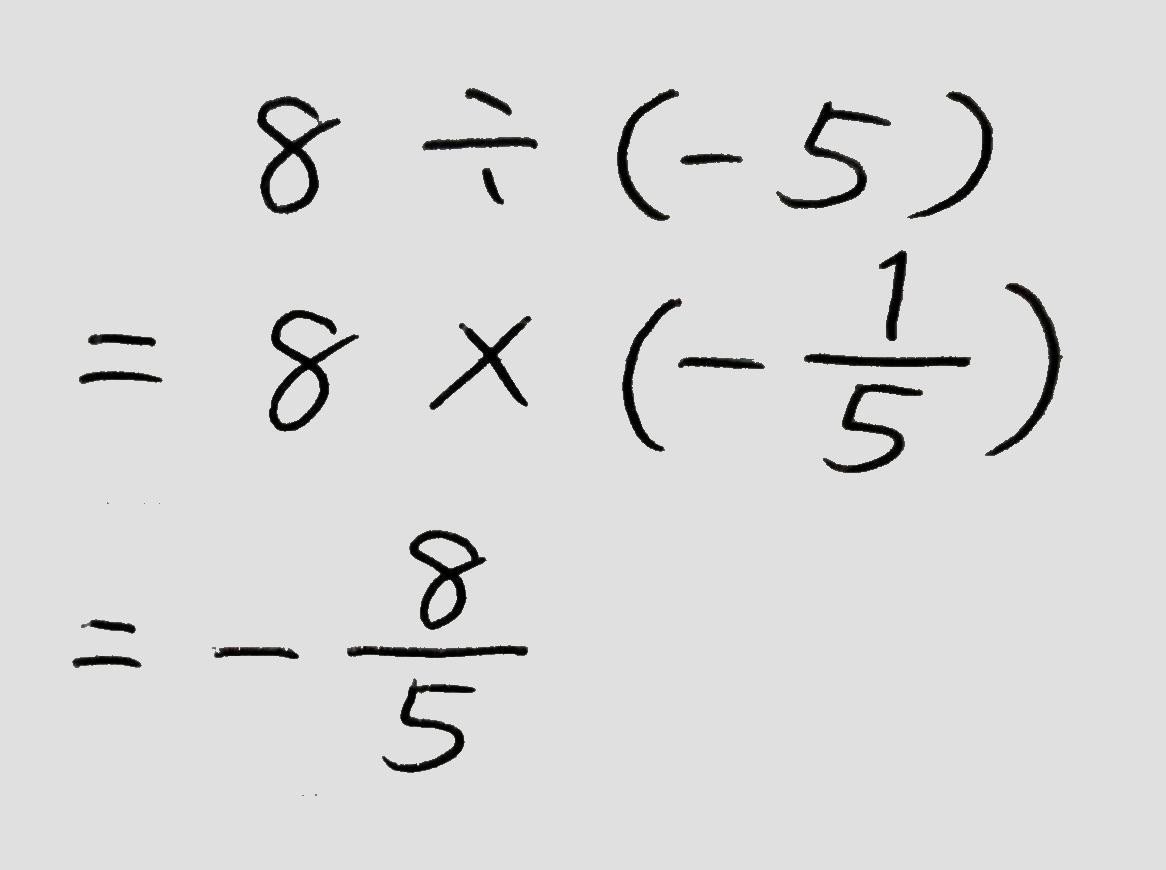
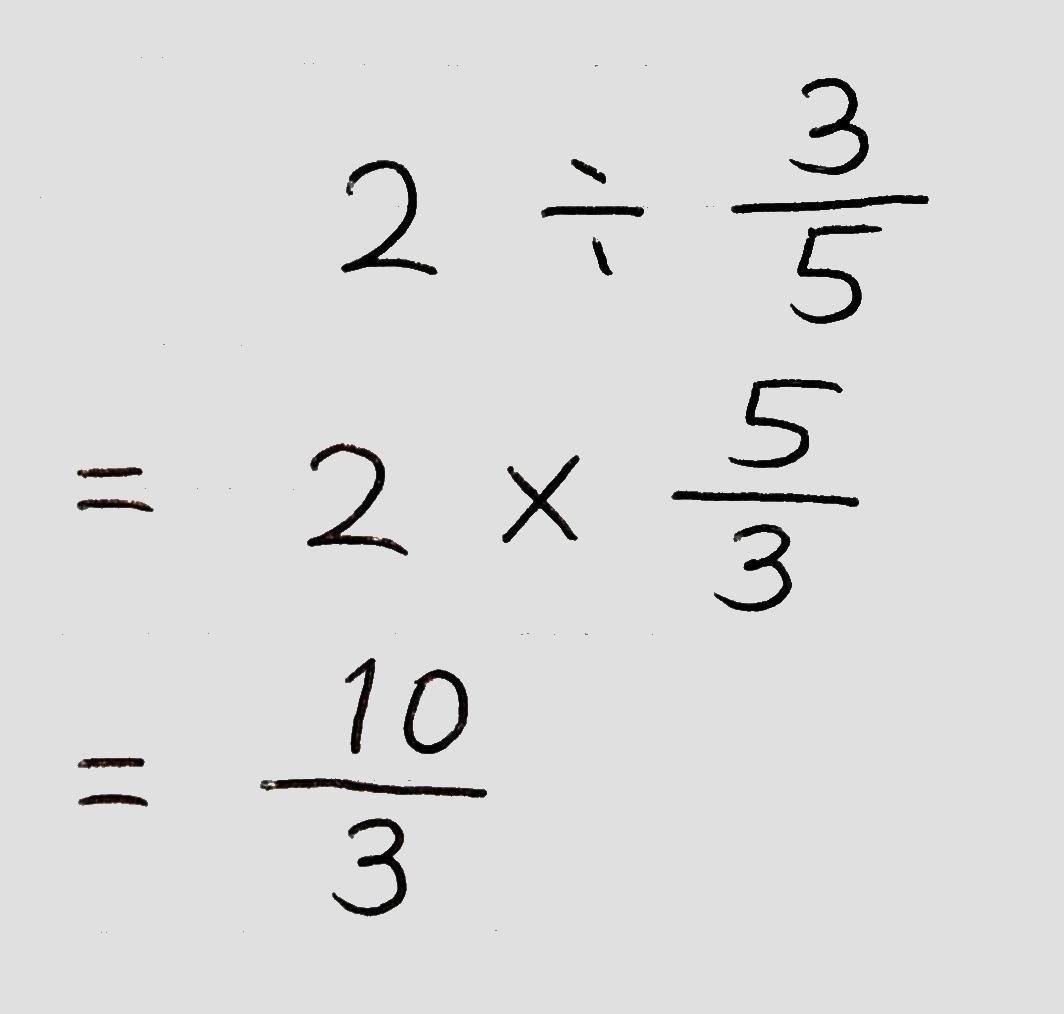
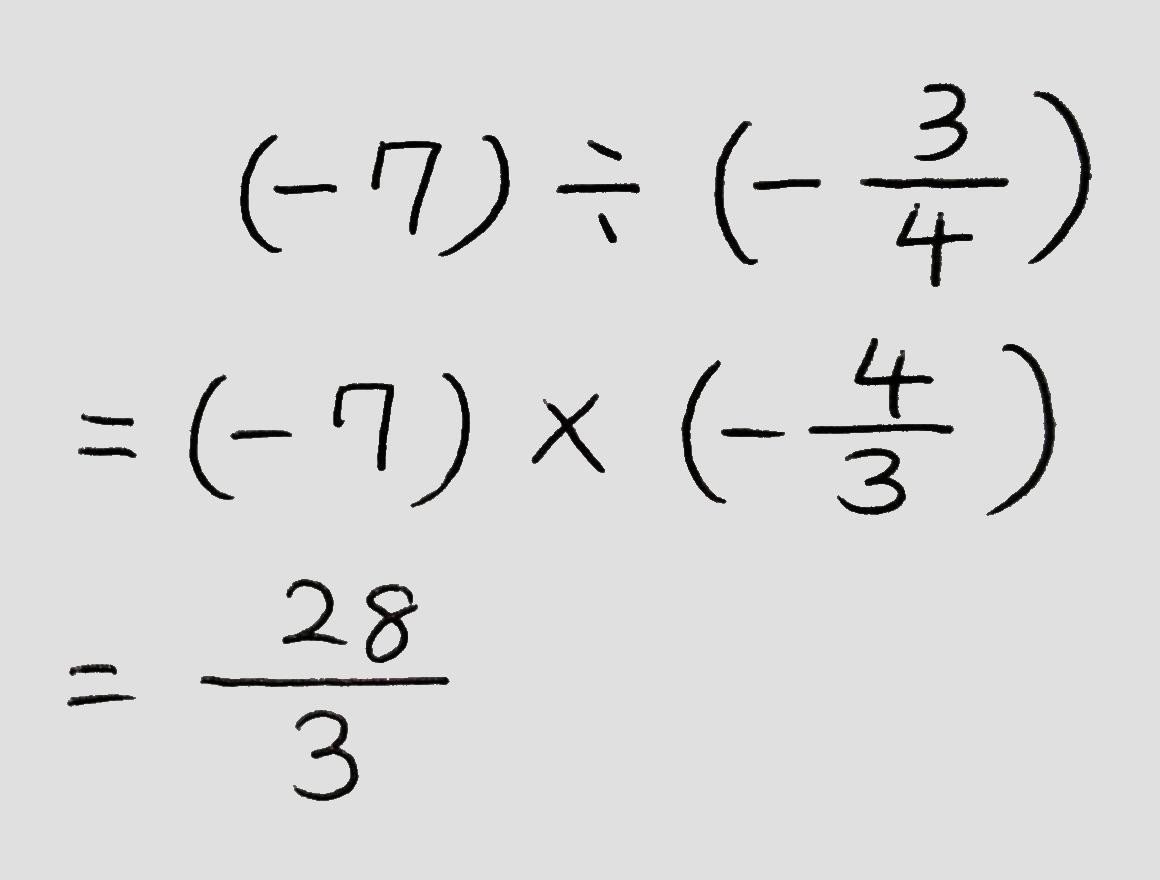
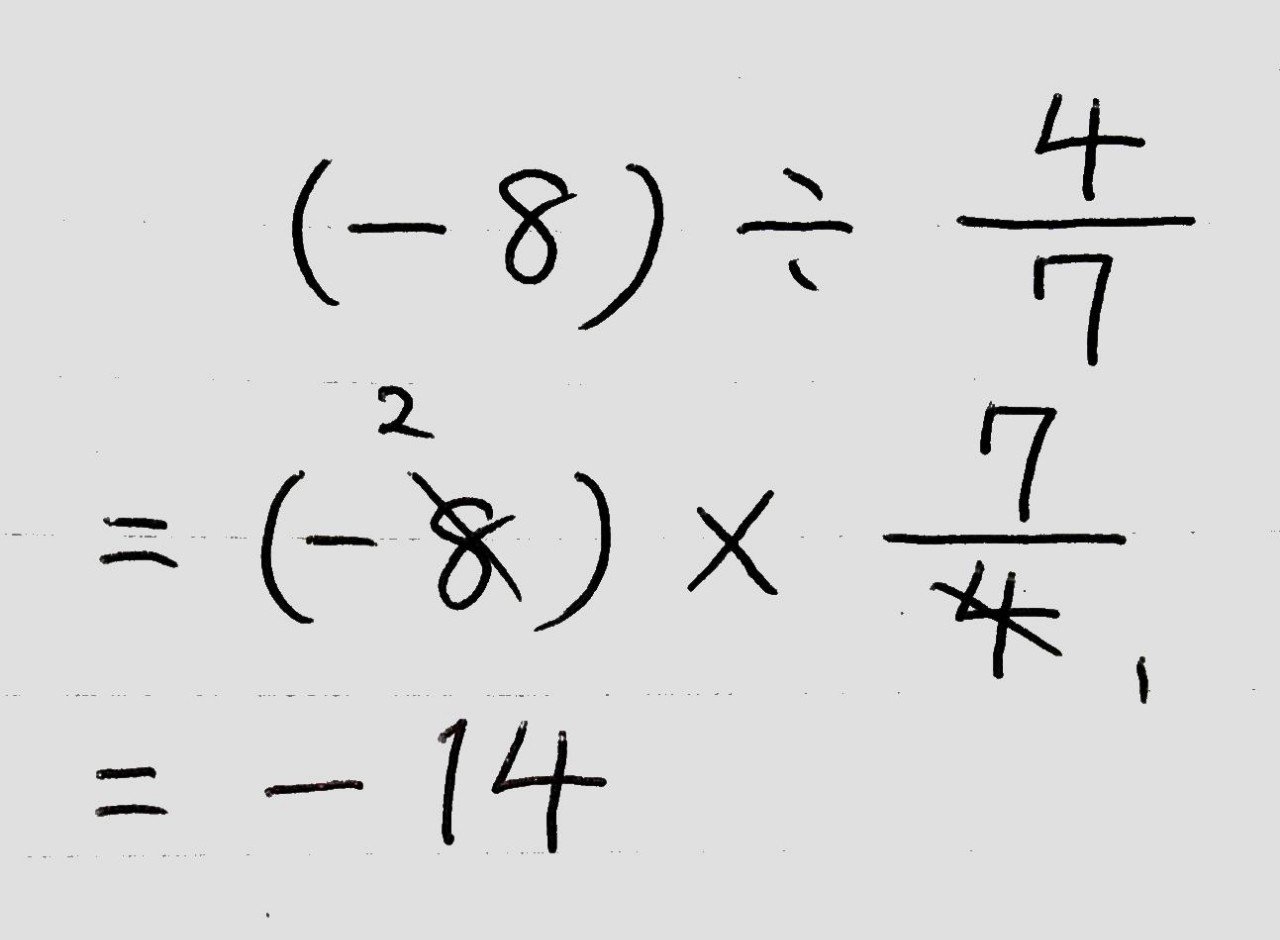
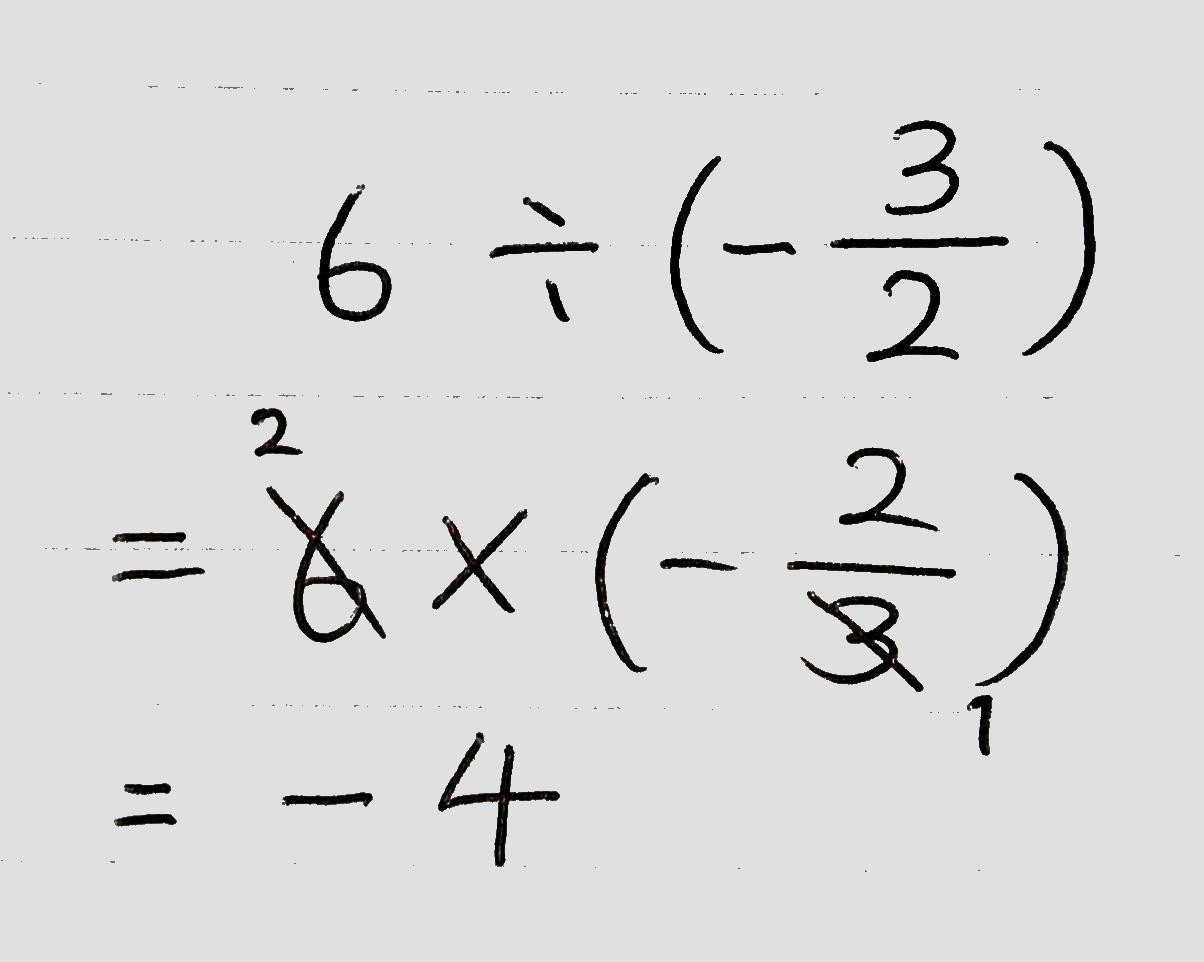
乗法と除法の混じった計算
○まず、除法を乗法に変え、乗法だけの式になおします。次に符号を決めます。「3数以上の乗法」でまとめたように、
負の符号が偶数個なら、積の符号は+
負の符号が奇数個なら、積の符号は−
です。符号が決まったら、あとは計算するだけです。
(例題)
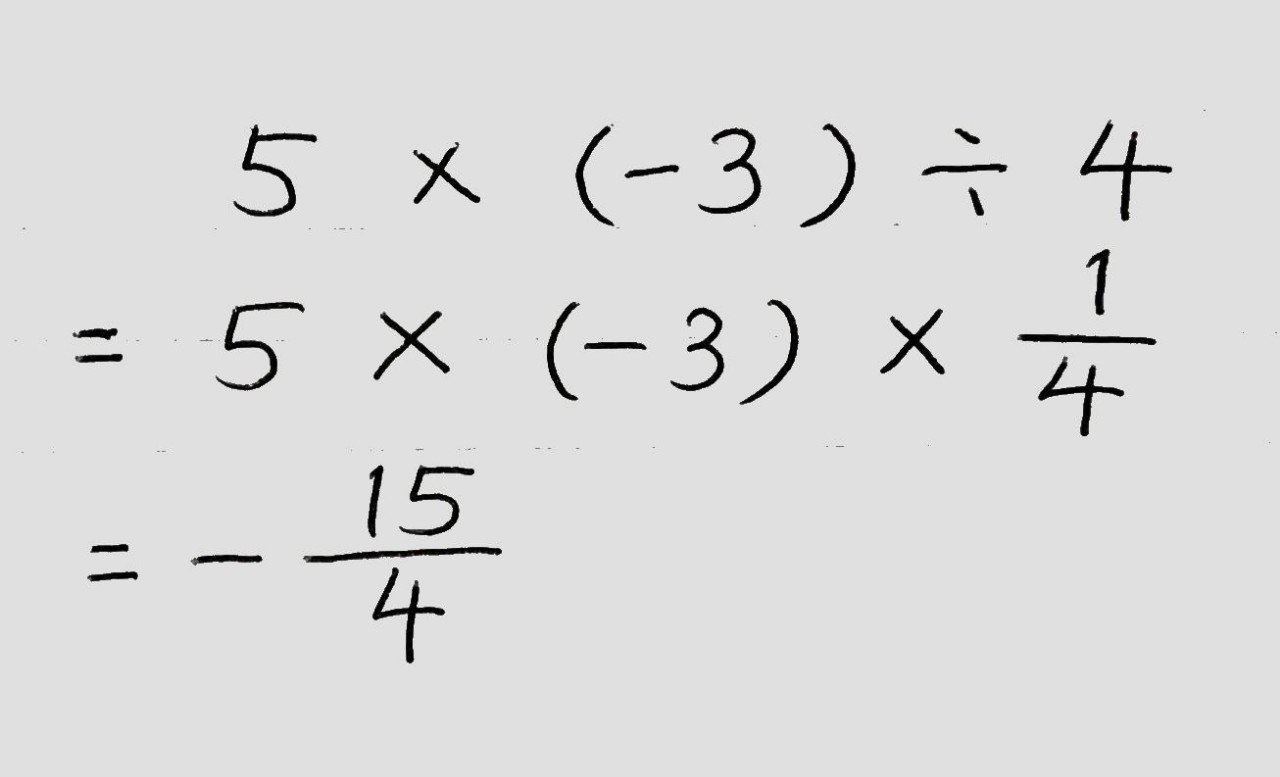
※上の解き方を少し発展させると次のような解き方も。全体を分数の形に変換し、「÷○」を分母に、頭の項と「×○」を分子に……という書き方で解くこともできます。
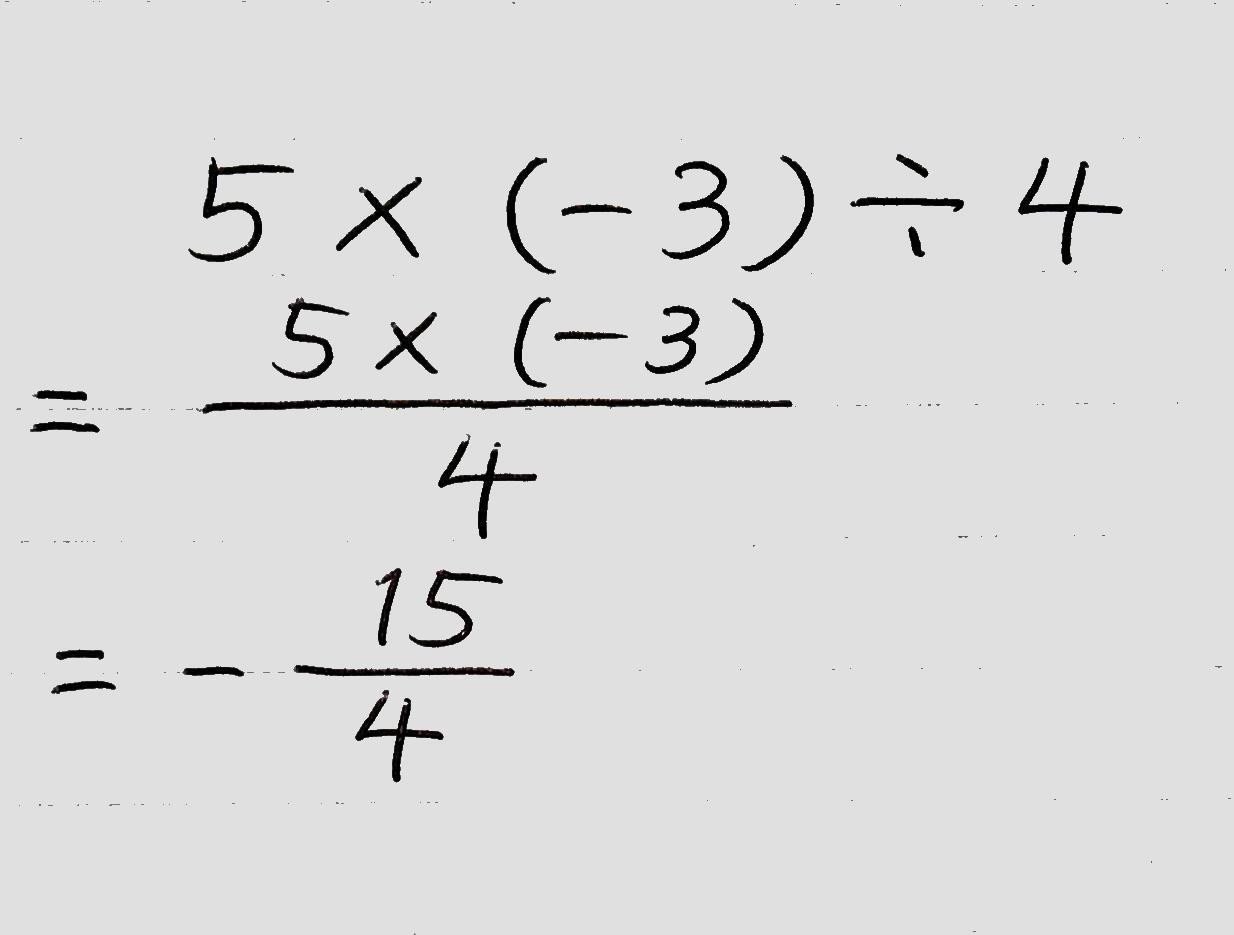
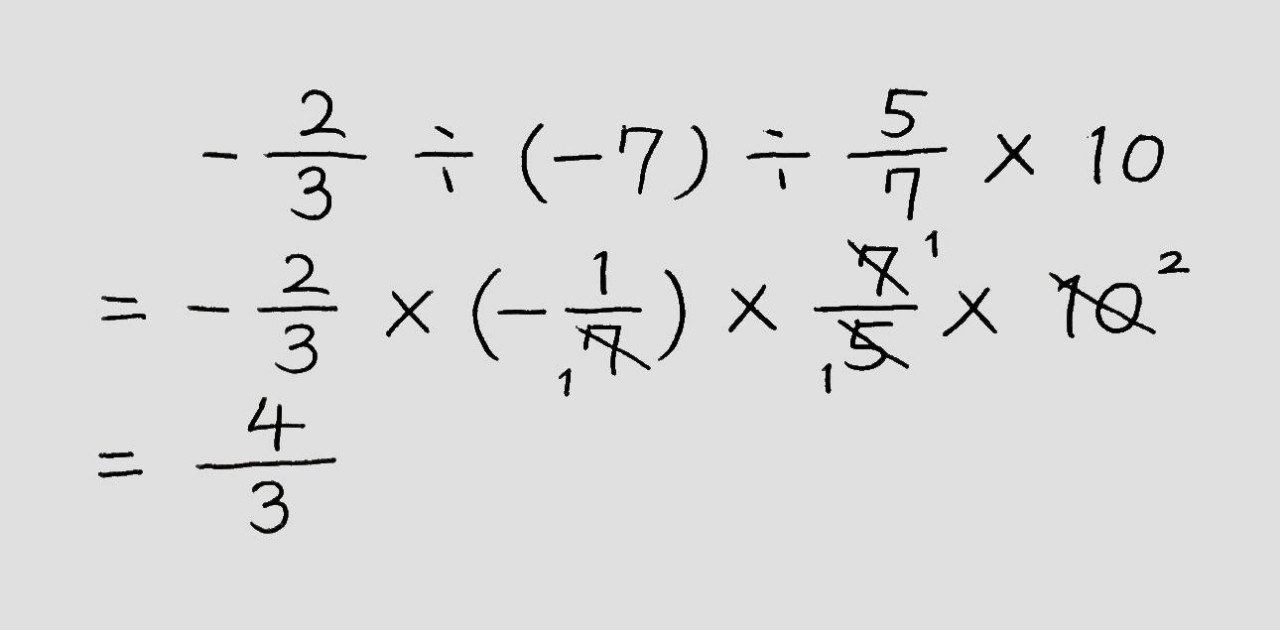
四則の混じった計算
○加法・減法・乗法・除法が混じった計算は、
①乗法・除法の計算を先に。
②残った加法・減法を計算。
(例題)
3+5×7
=3+35
=38
↑5×7から先に計算します。
10÷5−2×6
=2−12
=−10
↑先に10÷5と2×6を計算します。
○かっこのある式の計算は、かっこの中の計算を優先します。
(例題)
(3+5)×7
=8×7
=56
↑乗法・除法より、さらに優先度が高くなるのがかっこの中の計算です。なので、(3+5)のほうを先に計算します。
−10×{5−(2−4)}
=−10×{5−(−2)}
=−10×(5+2)
=−10×7
=−70
↑かっこの中にもかっこがあるときは、内側のかっこが優先です。
※内側のかっこは( )、外側のかっこは{ }……といった感じで、使うかっこの形もちょっとした決まりがあります。
○累乗のある式の計算は、基本的に累乗が先になります(かけ算なので)。ただし、累乗もかっこもある式の計算の場合は、どこに指数が付いているかによって順番が変わってきます。
(例題)
3+5×7²
=3+5×49
=3+245
=248
3²+5×7
=9+35
=44
(3+5²)×7
=(3+25)×7
=28×7
=196
↑かっこの中の数に指数が付いているときは、その累乗の計算を先にします。
(3+5)²×7
=8²×7
=64×7
=448
↑かっこのすぐ外側に指数が付いているときは、先にかっこの中の計算をします。
分配法則
○いきなりですが、まずこちらの例題を見てください。
(例題)
(3+5)×7
=8×7
=56
3×7+5×7
=21+35
=56
↑上の2つの例題は、どちらも答えが同じですよね。このような式の計算は、
(a+b)×c=a×c+b×c
a×(b+c)=a×b+a×c
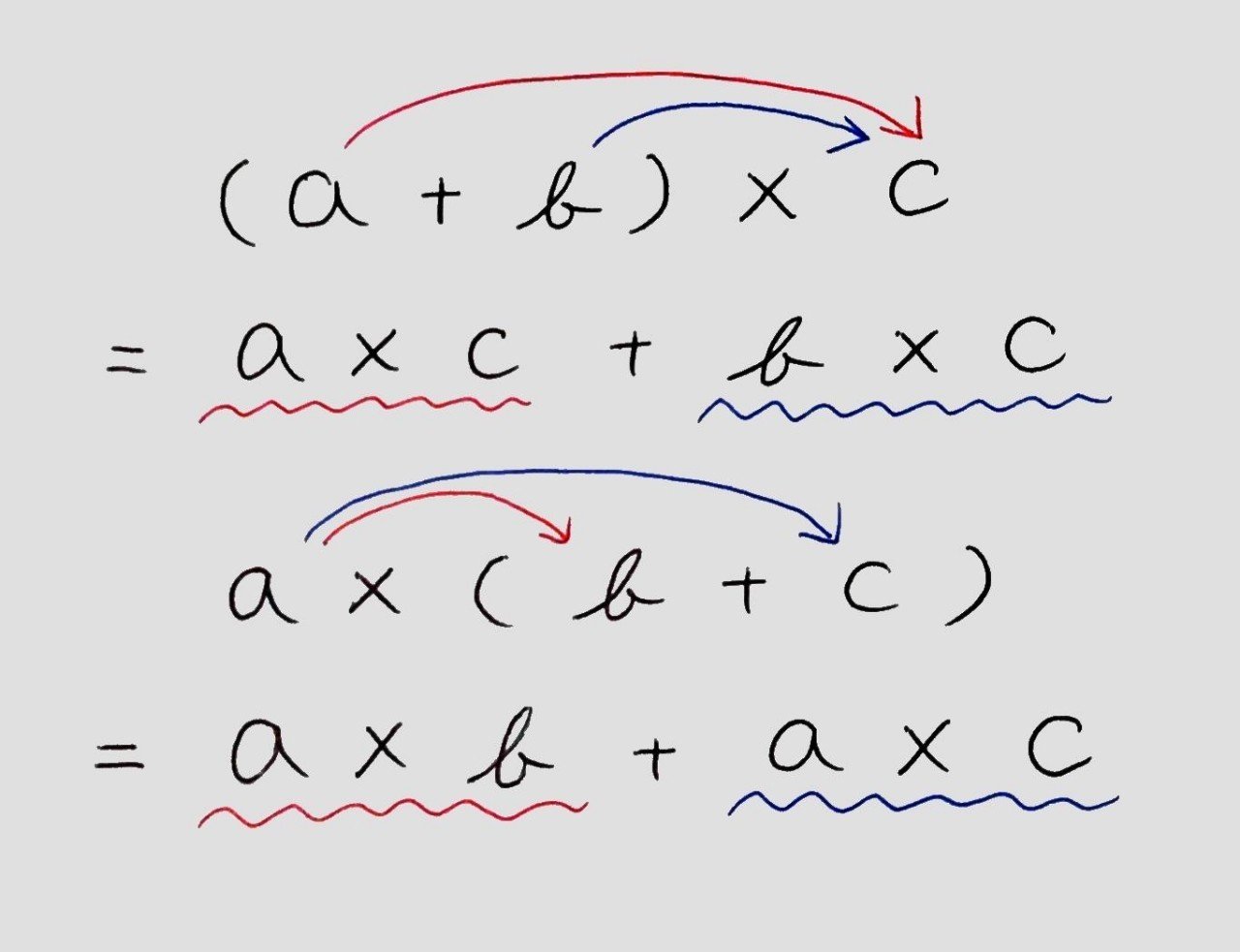
が成り立ちます。このような計算の法則を分配法則(ぶんぱいほうそく)といいます。
(例題)
(−2−4)×(−6)
=(−2)×(−6)+(−4)×(−6)
=12+24
=36
※分配法則を使わずに、かっこの中から先に解くと、
(−2−4)×(−6)
=(−6)×(−6)
=36
25×6+25×4
=25×(6+4)
=25×10
=250
※分配法則を使わずに、乗法から先に解くと、
25×6+25×4
=150+100
=250
○定期テスト等では、解き方が指定されていたら指示どおりに、特に指定されていなかった自分が解きやすいほうの解き方で計算すると良いでしょう!より自分がミスしづらいほう、計算しやすいほうを見極めることが大切です。
別noteで、正負の数の単元で登場する用語についてまとめています。よろしければこちらもどうぞ。
いいなと思ったら応援しよう!

