青チャート数学Ⅲ 186番の解説
漸近線
まず、f(x)の漸近線が何か…は、わかっていますよね。
簡単に言えば、f(x)=g(x)ではないけど、かなりf(x)に近づくg(x)のことです。
漸近線の求め方のルート
y=f(x)について、
( ⅰ ) y→±∞ となる“定数“p (x座標)が存在するか調べる
( ⅱ ) x→±∞の時、y→k(定数)となるか調べる
( ⅲ ) f(x)/xの無限極限(=aとする)とf(x)-axの無限極限を調べる
まずは問題を見てみましょう。

結構面倒くさそうですよね。(それなのに星2とか…)
(1)を解く
では、(1)からいきましょう
(1)のように、

となっている問題は、
まずは

このように変形しましょう。(計算が楽になる)
今回は、

このように変形できます。
(i)に従って、y→±∞となる定数pを探します。
そこで、xの定義域に着目します
今回は、(x^2 -4)≠0ですから、x≠±2です。
しかし、もしxが±2にかなり近づいた値を取るとしたらどうなるか調べてみましょう。

つまり、定数p=±2です。←(A)
次に(ii)について、

となるので、定数kは存在しません。←(B)
最後に(iii)について、
なんと、x軸にもy軸にも並行でない漸近線について次のことが成り立ちます。

これを用いると、

a=1,b=0となります。←(C)
(A)(B)(C)より、
漸近線は、x=±2, y=x となります。
(2)を解く
では次は(2)ですが、することはほぼ同じです。
(i)と(ii)は簡単に書いておきます。
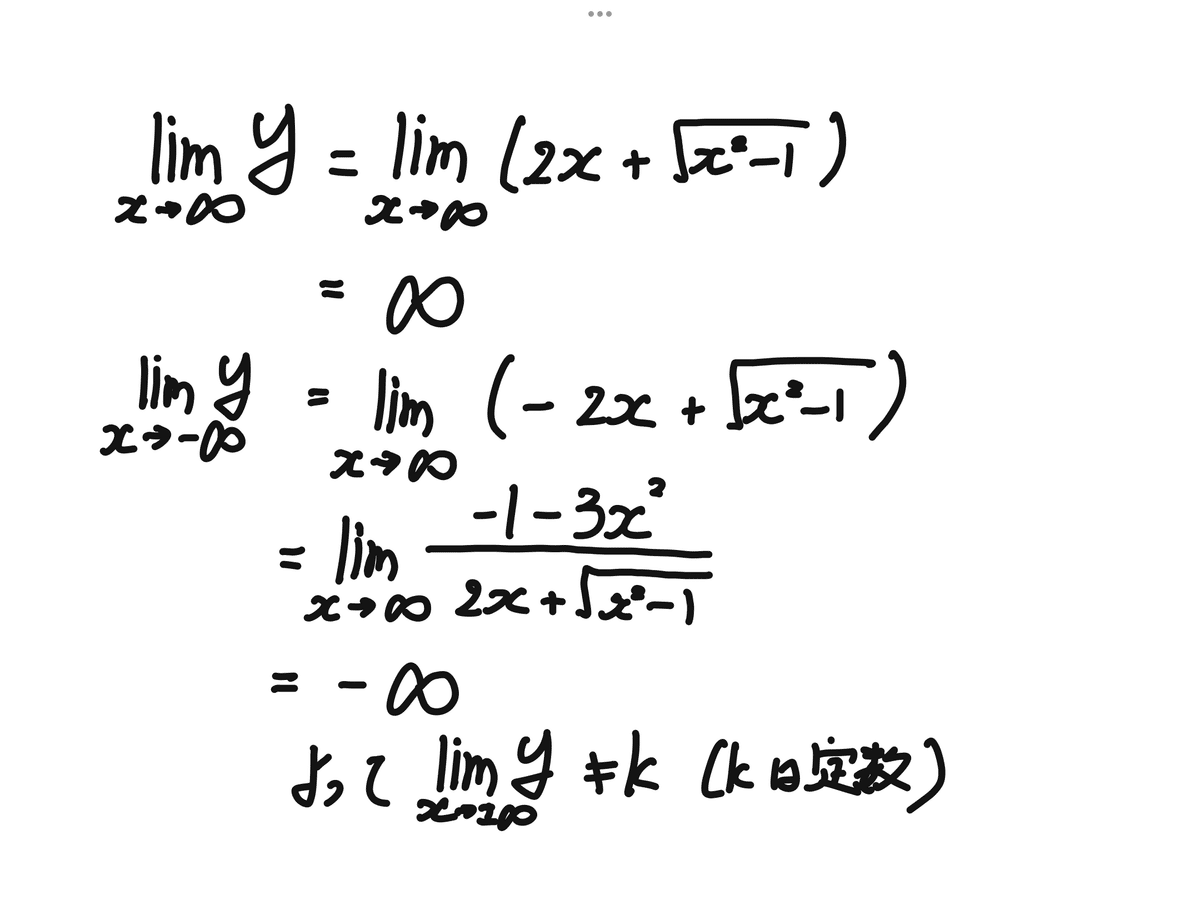

さて、問題は(iii)の時です。
今回は(1)と同じようにすんなり解けるかと思いきや、
(1)は極限値が1パターンずつだったのに対して今回は2パターンずつです。


そして考えられる漸近線(?)は以下の4通りです。

しかし、よく考えてみてください。
ウとエは切片が∞になっていますが、そんな漸近線はあり得ません。
よって、以上から漸近線は
y=3x, y=x
となります
ちなみに、最後のウとエが存在しないもう一つの理由が、xの取る値の範囲にあります。
x→∞なら当然0<xなので、aを求めるときにx→∞と置いたなら、bを求めるときもx→∞だけでいいのです。
