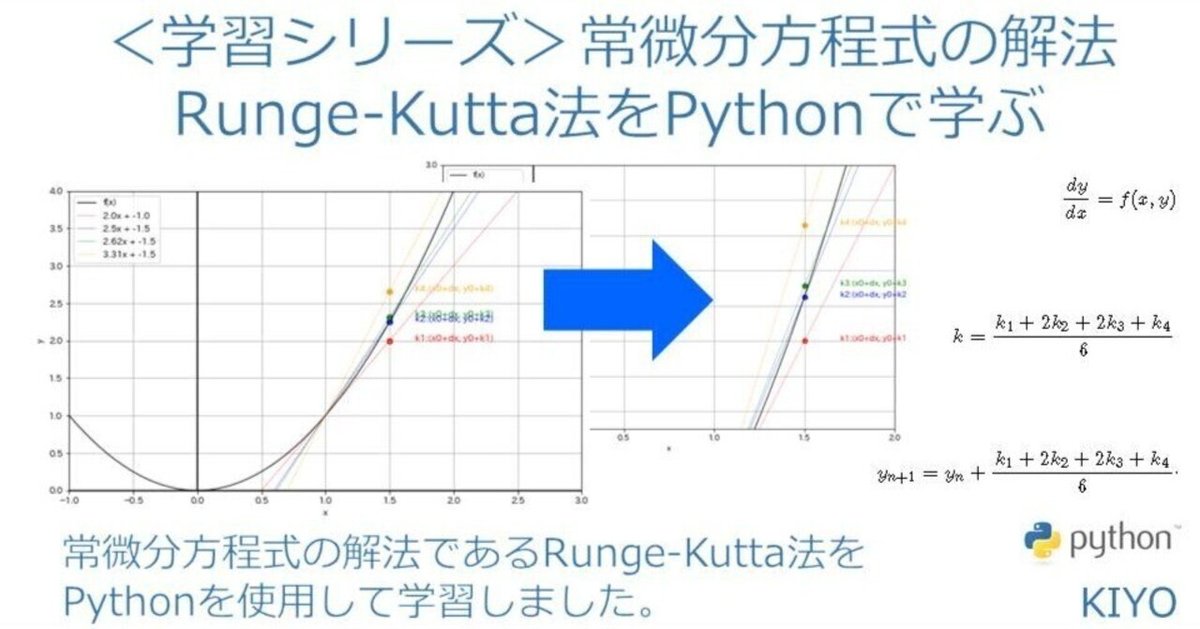
<学習シリーズ>常微分方程式の解法:Runge-Kutta法をPythonで学ぶ
1.概要
1-1.緒言
本記事は”学習シリーズ”として自分の勉強備忘録用になります。
常微分方程式の解法として下記手法がありますが、今回はRunge-Kutta法を説明します。
●Euler法:最もシンプルだが計算精度は低い
●Leap-Frog法:Euler法の時間単位を分割することで精度をあげた
●Runge-Kutta法:精度は高いが数式が複雑であり計算量も多い
1-2.サンプル問題
今回のサンプル問題は関数:$${y=f(x)=x^2}$$、初期値$${x_{0}=1.0}$$、微小変化量$${dx=0.5}$$において数値解法によりx=1.5におけるy=2.25を算出します(数式から簡単に求められるが理解のために簡単な式を使用)。
$$
f(x)=x^2 \\
f'(x)=2x \\
x=1の時、f(1)=1, f'(1)=2 \\
x=1.5の時、f(1.5)=2.25, f'(1.5)=3
$$
[IN]
def func(x):
return x**2
#初期値
x0, y0 = 1, func(1) #初期値
dx=0.5 #刻み幅
xs = np.linspace(-1, 5, 100) #プロット用のx軸データ
print(x0, y0)
[OUT]
1 12.Runge-Kutta法の理解
f(x)の微分$${\frac{dy}{dx}}$$を計算して微小変化dxをかければ変化量dyが求まります。ただし下記の通り$${x=x_{0}}$$の傾きを使用(Euler法)だと変化量が足りず、$${x=x_{0}+dx}$$の傾きを使用すると変化量が過剰になります。

X次のRunge-Kutta法では変化量$${k_{i}}$$をX個計算して(真値に近い変化量を)加重平均することでEuler法より高精度な計算をします。
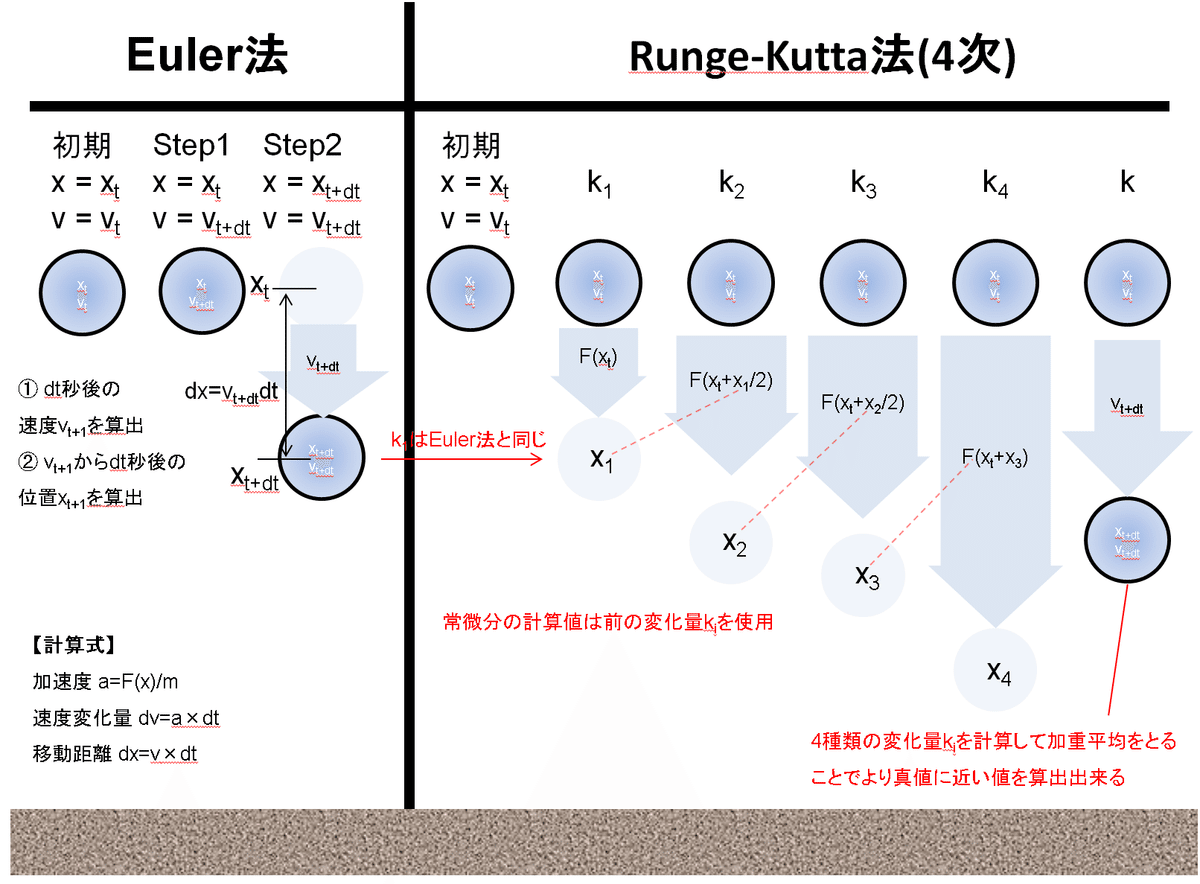
参考として自由落下問題(万有引力を考慮)時のEuler法とRunge-Kutta法の比較イメージは下図の通りです。オイラー法は1段1次のルンゲクッタ法とも呼ばれます。
2-1.基本式(4次のルンゲクッタ)
Runge-Kutta法には何種類かあり、4次のRunge-Kuttaは下記の通りです。
y:xの関数f(x)、dx:独立変数xの微小変化
$$
RungeKutta:y_{n+1}=y_{n}+\frac{k_{1}+2k_{2}+2k_{3}+k_{4}}{6}
$$
$$
dxにおける変化量dy:\frac{k_{1}+2k_{2}+2k_{3}+k_{4}}{6}
$$
$${k_{1}}$$:Euler法と同じ$${f(x+dx) = f(x) + f'(x)dx}$$であり一番小さい
$${k_{2}}$$:$${k_{1}}$$から推定して得られる変化量であり$${\frac{dx}{2}}$$の傾きが$${f(x_{n}+\frac{h}{2},y_{n}+\frac{k_{1}}{2})}$$(真値に近い)
$${k_{3}}$$:$${k_{2}}$$から推定して得られる変化量であり$${\frac{dx}{2}}$$の傾きが$${f(x_{n}+\frac{h}{2},y_{n}+\frac{k_{2}}{2})}$$(真値に近い)
$${k_{4}}$$:$${k_{3}}$$から推定して得られ$${x=x_{0}+dx}$$における傾きと近い値となり$${k_{i}}$$の中では最大値である。
【ポイント】
●$${k_{1}}$$はEuler法と同じ:残りの$${k_{i}}$$で補正させることでEuler法より高精度で推定が可能
●変化量は$${k_{1}}$$、 $${k_{2}}$$、$${k_{3}}$$、$${k_{4}}$$の順に大きくなり $${k_{2}}$$、$${k_{3}}$$は真値に近い
●4次では4種類の平均を算出する。 $${k_{2}}$$、$${k_{3}}$$は真値は真値に近いのでこの2つに重みがつくように加重平均をとる。
※$${k_{2}}$$、$${k_{3}}$$の係数が2であり全体を6で割るのは加重平均
2-2.変化量kiの詳細
2-2-1.kiの公式
Runge-Kutta法の各変化量$${k_{i}}$$は下記で表せます。
$$
RungeKutta:y_{n+1}=y_{n}+\frac{k_{1}+2k_{2}+2k_{3}+k_{4}}{6}
$$
$$
座標(x,y)での傾き(常微分方程式):\frac{dy}{dx}=f(x,y)
$$
$$
k_{1}= f(x_{0},y_{0})dx
$$
$$
k_{2}= f(x_{0}+\frac{dx}{2},y_{0}+\frac{k_{1}}{2})dx
$$
$$
k_{3}= f(x_{0}+\frac{dx}{2},y_{0}+\frac{k_{2}}{2})dx
$$
$$
k_{4}= f(x_{0}+dx,y_{0}+k_{3})dx
$$
【ポイント】
●$${k_{1}}$$はEuler法と同じであり$${f(x_{0},y_{0})=f'(x_{0})}$$と同じ
●$${k_{2}}$$は変化量dxの中央($${x_{0}+\frac{dx}{2}}$$)かつy=$${y_{0}+\frac{k_{1}}{2}}$$における傾きから算出(次項で補足)
2-2-2.常微分方程式の傾きの変換
ここが現在100%理解できていない部分となります。
上記で$${\frac{dy}{dx}=f(x,y)}$$と記載して、$${k_{2}= f(x_{0}+\frac{dx}{2},y_{0}+\frac{k_{1}}{2})dx}$$と記載しております。
f(x)の独立変数はxの一つなのに何故$${\frac{dy}{dx}=f(x,y)}$$になるのかが理解できておりませんが下記数式に展開できると思います。
関数f(x)に対して座標(x,y)における傾き$${\frac{dy}{dx}=f(x,y)}$$に対して、yの値を用いて$${f'(x)}$$の形にもっていくことができます。
$$
k_{1}= f(x_{0},y_{0})dx=f'(x_{0})
$$
$$
k_{2}= f(x_{0}+\frac{dx}{2},y_{0}+\frac{k_{1}}{2})dx =f'(x_{0}+\frac{k_{1}dx}{2})dx
$$
$$
k_{3}= f(x_{0}+\frac{dx}{2},y_{0}+\frac{k_{2}}{2})dx =f'(x_{0}+\frac{k_{2}dx}{2})dx
$$
$$
k_{4}= f(x_{0}+dx,y_{0}+k_{3})dx =f'(x_{0}+k_{3}dx)dx
$$
キーワードは中点法(修正オイラー法)、解曲線あたりだと思うのですが、明確に記載されている資料が確認できておりません。
http://www.slis.tsukuba.ac.jp/~fujisawa.makoto.fu/lecture/mic/text/08_derivative1.pdf
https://wwwnucl.ph.tsukuba.ac.jp/~hinohara/compphys2-18/doc/compphys2-11.pdf
3.Pythonコード
Pythonのコードに落とし込みます。今回は動作を理解するための関数を作成しておりRunge-Kuttaを直接計算するクラスは作成しておりません。
3-1.基礎条件・ライブラリインポート
まずは必要なライブラリのインポートや使用していく関数を作成します。
初期値は$${x_{0}}$$=1, $${y_{0}}$$=1、刻み幅dx=0.5(※$${y_{0}}$$はRunge-Kuttaの計算では使用しませんが①最終値の計算($${y_{n}=y_{0}+k_{i}}$$、②($${x_{0}}$$,$${y_{0}}$$)を通る線形プロットを作成するために出力しました。)
plot_line関数で線形プロットを記載
[IN]
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
def func(x):
return x**2
#初期値
x0, y0 = 1, func(1)
xs = np.linspace(-1, 5, 100)
dx=0.5 #刻み幅
x_next = x0 + dx #次のx座標
x_half = x0 + dx/2 #x0とx_nextの中間点
[OUT][IN]
def plot_line(xs, ys, ax, name, ls='-', c='blue', w=1.0):
ax.plot(xs,ys, label=name, linestyle=ls, color=c, linewidth=w)
ax.set(xlabel='x',
ylabel='y',
xlim=(-1,3),
ylim=(0,4))
[OUT]3-2.微分計算用のクラス:NumericalDiff
微分の計算や結果の出力をするクラスを作成しました。機能は下記の通り
インスタンス化時は指定の関数を引数に渡して、その他の計算は別途メソッドで実行させる。
numerical_diff:中心差分による傾きを計算
lin_regression:傾き、切片から線形プロット作成(可視化用)
labelmaker:MatPlotlibのラベルを作成するための関数(可視化用)
calc_slope:関数f(x)の$${x_{i}}$$における傾き$${f'(x_{i})}$$を算出
calc_intercept:note記事説明用として座標($${x_{0}}$$,$${y_{0}}$$)を通る傾き$${f'(x_{i})}$$をプロットするために、切片を計算する関数を作成
calc_diff:求めた傾きから各変化量$${k_{i}=f'(x_{i})dx}$$を算出
[IN]
#数値微分
class NumericalDiff:
def __init__(self, func):
self.func = func #f(x)
def numerical_diff(self, f, x):
h = 1e-4 #丸め誤差が出ない程度の小さな値
return (f(x+h) - f(x-h)) / (2*h)
def lin_regression(self, slope, intercept, xs):
return slope*xs + intercept
def labelmaker(self, slope, intercept):
slope, intercept = round(slope, 2), round(intercept, 1)
return f'{slope}x + {intercept}'
def calc_slope(self, x):
slope = self.numerical_diff(self.func, x) #座標xにおけるf(x)の傾き
return slope
def calc_intercept(self, x, y, slope):
intercept = y - slope*x
return intercept
def calc_diff(self, slope, dx):
return slope*dx #微分による傾きからdx変化したときの変化量
[OUT]3-3.動作確認
まずはシンプルな動作確認を実施します(※note説明用)。
[IN]
def plot_line(xs, ys, ax, name, ls='-', c='blue', w=1.0):
ax.plot(xs,ys, label=name, linestyle=ls, color=c, linewidth=w)
ax.set(xlabel='x',
ylabel='y',
xlim=(-0.5,3),
ylim=(-2,5))
#初期値
x0, y0 = 1, func(1) #初期値
dx=0.5 #刻み幅
xs = np.linspace(-1, 5, 100) #プロット用のx軸データ
# print(x0, y0)
#x=1における傾き
linear_func = NumericalDiff(func)
linear_func = NumericalDiff(func)
slope = linear_func.calc_slope(x0)
intercept = linear_func.calc_intercept(x0, y0, slope)
ys = linear_func.lin_regression(slope=slope,
intercept=intercept,
xs=xs)
#x=2(x0+dx)における傾き
x_next, _ = x0+dx, func(x0+dx)
linear_func2 = NumericalDiff(func)
slope_next = linear_func2.calc_slope(x_next)
intercept_next = linear_func2.calc_intercept(x0, y0, slope_next)
ys_next = linear_func2.lin_regression(slope=slope_next,
intercept=intercept_next,
xs=xs)
#可視化
fig = plt.figure(figsize=(10,6), facecolor='w')
ax = fig.add_subplot(111)
ax.plot([-10,10], [0,0], c='black', ls='-') #x軸を描写
ax.plot([0,0], [-10,10], c='black', ls='-') #y軸を描写
ax.set_yticks(np.arange(-2,5.5,0.5))
ax.set_ylim(-2,5)
plot_line(xs, func(xs) , ax, name='f(x)', c='black', w=1.0)
plot_line(xs, ys, ax,
name=f"f'(1)={linear_func.labelmaker(slope,intercept)}",
c='green', ls='--', w=0.5)
plot_line(xs, ys_next, ax,
name=f"f'(2)={linear_func2.labelmaker(slope_next,intercept_next)}",
c='blue', ls='--', w=0.5)
plt.grid()
plt.legend()
plt.show()
[OUT]
3-4.Runge-Kuttaの実装
Runge-Kutta法をスクラッチで実装します。手順は下記の通りです。
初期値:$${x=x_{0}}$$における傾き$${f'(x_{0})}$$からEuler法で$${k_{1}}$$を算出する
1つ目の変化量$${k_{1}}$$から変化量の中点$${\frac{dx}{2}}$$における傾き$${f(x_{0}+\frac{dx}{2},y_{0}+\frac{k_{1}}{2})=f'(x_{0}+\frac{k_{1}dx}{2})}$$を求める。その傾きにdxをかけて変化量を$${k_{2}}$$を算出する
2つ目の変化量$${k_{2}}$$から変化量の中点$${\frac{dx}{2}}$$における傾き$${f(x_{0}+\frac{dx}{2},y_{0}+\frac{k_{2}}{2})=f'(x_{0}+\frac{k_{2}dx}{2})}$$を求める。その傾きにdxをかけて変化量を$${k_{3}}$$を算出する
3つ目の変化量$${k_{3}}$$から全量変化$${x=x_{0}+dx}$$における傾き$${f(x_{0}+dx,y_{0}+k_{3})=f'(x_{0}+k_{3}dx)}$$を求める。その傾きにdxをかけて変化量を$${k_{4}}$$を算出する
最後に可視化します(①各$${k_{i}}$$で使用した傾きを用いて$${x_{0}}$$=1, $${y_{0}}$$=1を通過する線形プロットを引くことで変化量を可視化、②各$${k_{i}}$$の値がどこにあるかわかるよう散布図+テキスト追加
[IN]
def plot_line(xs, ys, ax, name, ls='-', c='blue', w=1.0):
ax.plot(xs,ys, label=name, linestyle=ls, color=c, linewidth=w)
ax.set(xlabel='x',
ylabel='y',
xlim=(-1,3),
ylim=(0,4))
#初期値
x0, y0 = 1, func(1)
xs = np.linspace(-1, 5, 100)
dx=0.5 #刻み幅
#k1
linf1 = NumericalDiff(func)
slope1 = linf1.calc_slope(x0)
intercept1 = linf1.calc_intercept(x0, y0, slope1)
ys1 = linf1.lin_regression(slope=slope1,
intercept=intercept1,
xs=xs)
k1 = linf1.calc_diff(slope1, dx)
#k2
linf2 = NumericalDiff(func)
x_k2 = x0 + k1/2*dx #k1の中間点:Runge-Kutta法のk2の計算に使う
slope2 = linf2.calc_slope(x_k2)
intercept2 = linf2.calc_intercept(x0, y0, slope2)
ys2 = linf2.lin_regression(slope=slope2,
intercept=intercept2,
xs=xs)
k2 = linf2.calc_diff(slope2, dx)
#k3
linf3 = NumericalDiff(func)
x_k3 = x0 + k2/2*dx #k2の中間点:Runge-Kutta法のk3の計算に使う
slope3 = linf3.calc_slope(x_k3)
intercept3 = linf3.calc_intercept(x0, y0, slope3)
ys3 = linf3.lin_regression(slope=slope3,
intercept=intercept3,
xs=xs)
k3 = linf3.calc_diff(slope3, dx)
#k4
linf4 = NumericalDiff(func)
x_k4 = x0 + k3*dx #k2の中間点:Runge-Kutta法のk4の計算に使う
slope4 = linf4.calc_slope(x_k4)
intercept4 = linf4.calc_intercept(x0, y0, slope4)
ys4 = linf4.lin_regression(slope=slope4,
intercept=intercept4,
xs=xs)
k4 = linf4.calc_diff(slope4, dx)
#可視化
fig = plt.figure(figsize=(10,6), facecolor='w')
ax = fig.add_subplot(111)
ax.plot([-10,10], [0,0], c='black', ls='-') #x軸を描写
ax.plot([0,0], [-10,10], c='black', ls='-') #y軸を描写
#線形プロット
plot_line(xs, func(xs) , ax, name='f(x)', c='black', w=1.0)
plot_line(xs, ys1, ax,
name=f"{linf1.labelmaker(slope1,intercept1)}", c='red', ls='--', w=0.5)
plot_line(xs, ys2, ax,
name=f"{linf2.labelmaker(slope2,intercept2)}", c='blue', ls='--', w=0.5)
plot_line(xs, ys3, ax,
name=f"{linf2.labelmaker(slope3,intercept2)}", c='green', ls='--', w=0.5)
plot_line(xs, ys4, ax,
name=f"{linf2.labelmaker(slope4,intercept2)}", c='orange', ls='--', w=0.5)
#k1の描写
y_next_k1 = linf1.calc_diff(slope1, dx)
plt.scatter(x0+dx, y0+y_next_k1, color='red')
plt.text(x0+dx+0.2, y0+y_next_k1, f'k1:(x0+dx, y0+k1)', color='red')
#k2の描写
y_next_k2 = linf2.calc_diff(slope2, dx)
plt.scatter(x0+dx, y0+y_next_k2, color='blue')
plt.text(x0+dx+0.2, y0+y_next_k2, f'k2:(x0+dx, y0+k2)', color='blue')
# #k3の描写
y_next_k3 = linf3.calc_diff(slope3, dx)
plt.scatter(x0+dx, y0+y_next_k3, color='green')
plt.text(x0+dx+0.2, y0+y_next_k3, f'k3:(x0+dx, y0+k3)', color='green')
# #k4の描写
y_next_k4 = linf4.calc_diff(slope4, dx)
plt.scatter(x0+dx, y0+y_next_k4, color='orange')
plt.text(x0+dx+0.2, y0+y_next_k4, f'k4:(x0+dx, y0+k4)', color='orange')
plt.grid()
plt.legend()
plt.show()
print(f'k1={k1:.3f}, k2={k2:.3f}, k3={k3:.3f}, k4={k4:.3f}, k={(k1+2*k2+2*k3+k4)/6:.3f}, 解析解={func(x0+dx)-func(x0):.3f}')
[OUT]
k1=1.000, k2=1.250, k3=1.312, k4=1.656, k=1.297, 解析解=1.250

結果より下記が確認できます。
4種類の変化量:$${k_{i}}$$が得られ得られ特に$${k_{2}}$$, $${k_{3}}$$の精度が高い。$${k_{2}}$$, $${k_{3}}$$に対して加重平均をとっているため真値に近い値が算出できている。
増加量の真値=1.250に対して計算増加量=1.297であり比較的高い精度で予想できている。
[IN]
import pandas as pd
import seaborn as sns
datas = {'name':['k1', 'k2', 'k3', 'k4', 'k', '真値'],
'value':[k1, k2, k3, k4, (k1+2*k2+2*k3+k4)/6, func(x0+dx)-func(x0)]}
df = pd.DataFrame(datas)
sns.barplot(data=df, x='name', y='value')
[OUT]
4.補足資料
4-1.刻み幅dxが大きい場合
先ほどはdx=0.5で非常に高精度の計算が出来ました。次にdx=1.0で計算してみます。
結果は下記の通り真値3に対して計算増加量k=6であり、理論値から2倍ずれる結果となりました。微分の大原則は「微小区間における変化」のためRunge-Kutta法をの精度が高くても刻み幅hの設定が悪いとまともな結果が出ないことが分かります。
[IN]
dx=1.0
~~~~~~その他同じ~~~~~~
print(f'k1={k1:.3f}, k2={k2:.3f}, k3={k3:.3f}, k4={k4:.3f}, k={(k1+2*k2+2*k3+k4)/6:.3f}, 解析解={func(x0+dx)-func(x0):.3f}')
[OUT]
k1=2.000, k2=4.000, k3=6.000, k4=14.000, k=6.000, 解析解=3.000
4-2.簡単な関数を使用した動作検証
最も簡単な関数で動作検証をしてみます。結論は前節と同じで「刻み幅hの設定が悪いとまともな結果が出ない」です。
例題として関数$${y=f(x)=x^2}$$を使用します。Euler法とRunge-Kutta法を使用して「微分$${f'(x)}$$のみを使用してf(x)の動作を再現」します。
下図に各アルゴリズムの動作イメージを記載しました。記載の通り今回の例ではEuler法は必ずf(x)の下を沿うような動作になります。
$$
y=f(x)=x^2 \\
f'(x) =\frac{dy}{dx}= 2x
$$

細かいコード説明はしませんので内容だけ下記記載します。
$${f(x)=x^2}$$と微分の$${f'(x)=2x}$$の関数を用意する
刻み幅dxを何パターン化で計算してEuler法とRunge-Kutta法の動作を確認する。
[IN]
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from typing import List, Dict
#関数の定義
def func(x):
return x**2 #f(x)=x^2
def diff_func(x):
return 2*x #f'(x)=2x
dx = 0.5 #刻み幅
xs = np.array([i*dx for i in range(50)])
y0 = func(xs[0]) #初期値
y = y0
y_cal = []
#Euler方
for x in xs:
y_cal.append(y)
y += diff_func(x)*dx #yの更新
#Runge Kutta法
class RungeKutta:
def __init__(self, dx, diff_func, log_verbose=True):
self.dx = dx
self.diff_func = diff_func
self.log_verbose = log_verbose #ログ出力の有無
self.output = {'k1':[], 'k2':[], 'k3':[], 'k4':[], 'k':[]}
def step_k(self, x):
k1 = self.diff_func(x)*self.dx
k2 = self.diff_func(x + k1/2*self.dx)*self.dx
k3 = self.diff_func(x + k2/2*self.dx)*self.dx
k4 = self.diff_func(x + k3*self.dx)*self.dx
#k:Runge-Kutta法による加重平均
k = (k1 + 2*k2 + 2*k3 + k4)/6
#結果の格納
if self.log_verbose:
self.logging_data(self.output, {'k1':k1, 'k2':k2, 'k3':k3, 'k4':k4, 'k':k})
return k
def logging_data(self, datas:List, params:Dict):
for key, value in params.items():
datas[key].append(value)
rungekutta = RungeKutta(dx=dx, diff_func=diff_func)
y = y0 #yの初期値
y_cal_runge = []
for x in xs:
y_cal_runge.append(y)
dy = rungekutta.step_k(x) #刻み幅hにおける変化量dyを出力
y += dy
fig = plt.figure(figsize=(10, 5), facecolor='white')
plt.plot(xs, func(xs), label='y=x^2')
plt.plot(xs, y_cal, label='Euler法', linestyle='dashed')
plt.plot(xs, y_cal_runge, label='Runge-Kutta法', linestyle='dashed')
# plt.xticks(xs)
# plt.xlim(0, 5); plt.ylim(0, 40)
plt.grid(); plt.legend(); plt.text(0.1, max(func(xs))/2, f'刻み幅h:{dx:.1f}', fontsize=14)
plt.savefig(f'savedata/EulerとRunge比較_h={dx:.1f}.png')
plt.show()
[OUT]
Runge-Kutta法ではEuler法のように必ず下は通らず、最初の方は比較的良い精度ですが、刻み幅が大きいと正しい結果は得られませんでした。
参考資料
あとがき
数式って情報を圧縮できるけど展開するための説明がないと使えないと思うのだが・・・・・
