Pythonで学ぶ統計学3:確率変数と確率分布
1.概要
本記事は統計学の学習記録用として作成しており、私が理解するのに時間がかかった場所や追って参照したい内容を中心にまとめております。
本記事のテーマは「確率変数と確率分布」になります。なお資料として下記(CC-BY)を参考にさせていただきました。
1-1.確率/確率分布とは
確率とは「事象がどの程度起きそうか」という度合いであり、確率分布は「ある試行で起こり得るすべての事象の確率を出力する関数」です。
確率分布を考える上でのポイントは下記の通りです。
記述統計では「得られたデータが全て(母集団)として計算」しましたが、標本抽出では無作為に抽出するため統計量が変化します。つまり得られる結果は(確率)分布として存在します。
自然現象としてある事象は確率分布に従うものが多いです。つまり自然現象などを確率モデルとして扱うことが出来ます。
1-2.記事説明:データとPythonライブラリ
本記事で使用したサンプルデータを紹介します。またPythonも使用していきますがライブラリの詳細説明は省きますので個別のライブラリは別記事で確認お願いします。なおScipyは(2023年1月現在)では記事を作成しておりませんがこちらも説明は省きます。
2.母集団と標本
次の記事で「推測統計学」を説明していますが、推測統計学には確率密度分布と母集団・標本の理解が重要になります。
母集団・標本は別記事にまとめましたのでご確認ください。
3.確率と確率変数
確率と確率変数について簡単に紹介します。
3-1.確率・確率変数・期待値・分散
各用語の意味は下記の通りです。
確率:物事を起こる偶然具合であり全事象の合計値は1となる。
確率変数:ある現象がいろいろな値を取り得るとき、取り得る値全体
期待値:確率とその事象で得られる値をかけたものの合計
分散:平均値との差の2乗
データの種類として、サイコロのようなとびとびの値をとる離散値と、身長のように連続的な値をとる連続値があります。各値の数式はデータの種類によって異なります。
3-2.離散型確率の数式
離散型における各項目の計算式は下記の通りです。なお$${X}$$は確率変数となります。
$$
確率関数p(x)=P(X=x)
$$
$$
期待値 \displaystyle E [X]=\sum_x x p(x)
$$
$$
分散Var(X) = E[(X-E(X))^2] = \sum_x (x-E(X))^2 p(x)
$$
【例1:サイコロを振る】
サイコロの例では下記の通りです。
$$
E(X) = \sum_x x p(x) = \frac{1}{6}\sum_{x=1}^6 x = \frac{1}{6}(1+2+3+4+5+6) = 3.5
$$
$$
\begin{aligned}
Var(X) &= E[(X-E(X))^2] \\ &= \sum_x (x-E(X))^2 p(x) \\ &= \frac{1}{6}[(1-3.5)^2 + (2-3.5)^2 + (3-3.5)^2 + (4-3.5)^2 + (5-3.5)^2 + (6-3.5)^2] \\ &= \frac{35}{12} \\ &\approx 2.9167
\end{aligned}
$$

3-3.連続型確率変数の数式
連続型における各項目の計算式は下記の通りです。
なお$${X}$$:確率変数、$${x}$$:データの値、$${\mu}$$:平均値、$${E(X)}$$:期待値、$${\sigma^2}$$:分散、$${f(x)}$$:確率密度関数(確率変数vs確率密度)です。
$$
確率密度関数f(x)の特性:\int_{-\infty}^{\infty} f(x) dx = 1
$$
$$
\mu=E(X) = \int_{-\infty}^{\infty} x f(x) dx=\int_{-\infty}^{\infty} (データ値 \times 確率密度) dx
$$
$$
\sigma^2 = E[(X-E(X))^2] = \int_{-\infty}^{\infty} (x-E(X))^2 f(x) dx
$$
$$
別Ver:\sigma^2 = E[(X - \mu)^2] = \int_{-\infty}^{\infty} (x - \mu)^2 f(x) dx=\int_{-\infty}^{\infty} ((データ値 - 平均値)^2 \times 確率密度) dx
$$
【例1_降水量:標本データ】
まず初めによくある標本データとして記述統計学的に考えてみます。降水量は連続値のため正確には確率分布を使用するのですが、とりあえずどの降水量でも同じ確率(密度)で出現すると仮定した一様分布で計算してみます(結果的には離散値と同じ扱いになってます)。
結果として記述統計量と同じ結果が得られました。
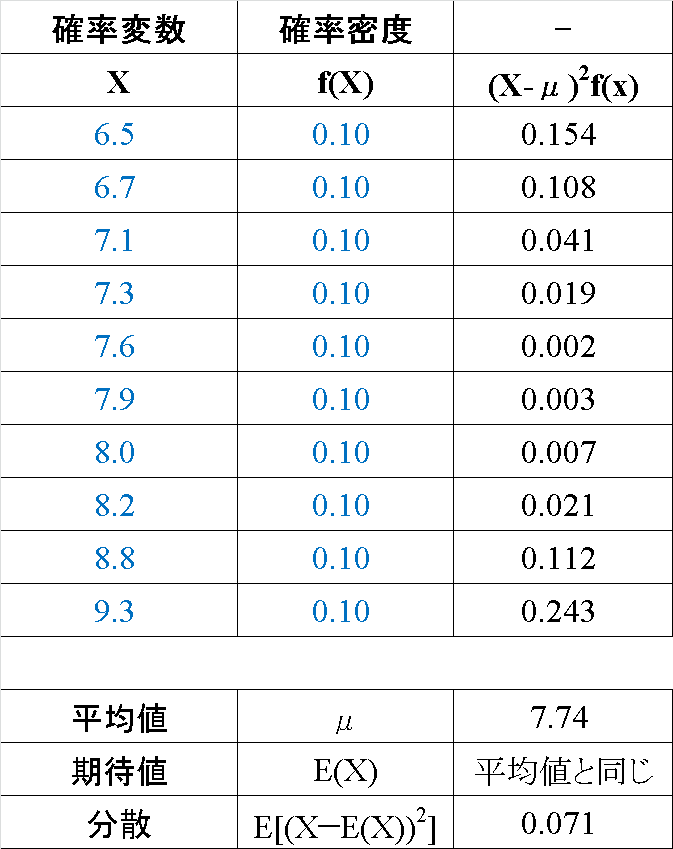
【例2_身長:確率密度分布】
次に身長の例として、データが正規分布(連続値の確率密度分布)として得られた時を考えます。
$$
正規分布:\mathcal{N}(x|μ, \sigma^2)=\dfrac{1}{\sqrt{2\pi\sigma^2}}\exp(-\dfrac{(x-\mu)^ 2}{2\sigma^ 2})
$$
身長の平均値$${\mu}$$165cm, 標準偏差$${\sigma}$$10cmとしたとき、期待値$${E(X)}$$は平均値と同じになるため165cmとなり、分散は$${\sigma^2}$$のため100となります。
(平均値$${\mu}$$は正規分布で仮定済みのため計算は不要)
$$
f(x) = \frac{1}{\sqrt{2\pi\cdot(10)^2}} e^{-\frac{(x - 165)^2}{2\cdot(10)^2}}
$$
3-4.正規分布における平均値=期待値の証明
連続型データの代表である正規分布(確率密度分布)において平均値$${\mu}$$=期待値$${E(X)}$$である証明をしたいと思います。
$$
f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x - \mu)^2}{2\sigma^2}}, E[X] = \int_{-\infty}^{\infty} x f(x) dx
$$
期待値$${E(X)}$$に確率密度関数$${f(x)}$$を代入します。
$$
E[X] = \int_{-\infty}^{\infty} x \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x - \mu)^2}{2\sigma^2}} dx
$$
この積分を解くために変数変換を行います。$${u = \frac{x - \mu}{\sigma}}$$とおくと、$${x = \sigma u + \mu}$$、$${dx = \sigma du}$$です。
$$
E[X] = \frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^{\infty} (\sigma u + \mu) e^{-\frac{1}{2}u^2} \sigma du
$$
$$
=\frac{\sigma}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^{\infty} u e^{-\frac{1}{2}u^2} du + \frac{\mu}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^{\infty} e^{-\frac{1}{2}u^2} du
$$
$$
=0 + \mu \cdot \frac{1}{\sqrt{2\pi\sigma^2}} \sqrt{2\pi\sigma^2} = \mu
$$
これより正規分布において$${E[X] = \mu}$$となります。
4.確率分布の基礎
4-1.確率分布とは
記述統計ではデータ(事実)をそのまま使用しましたが、標本には分布があるためデータ(定数)ではなく確率(分布)が重要となります。推測統計では分布を使用して標本から母集団の統計量を確率的に推定します。
得られるデータ(確率変数)の確率(密度)を分布で表現した関数を確率分布と呼びます。
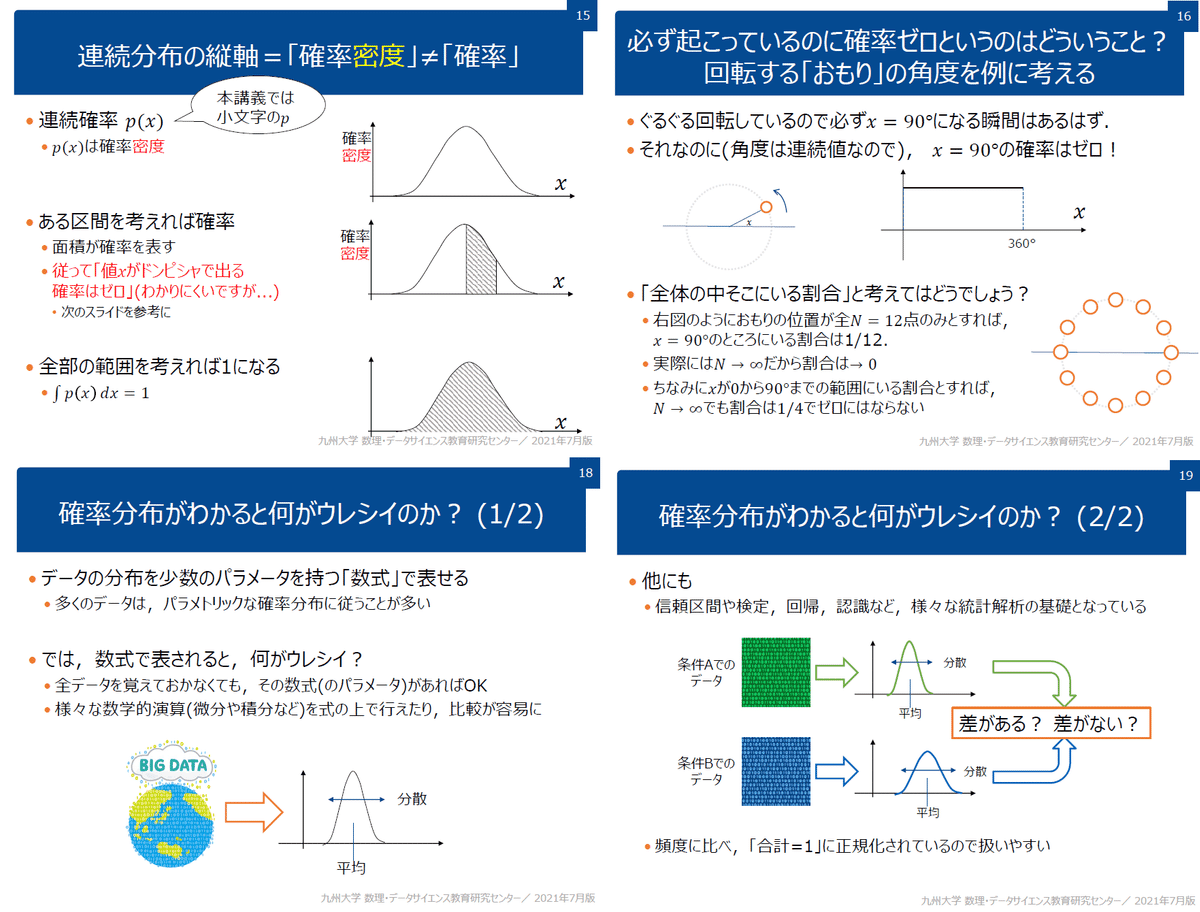
4-2.確率分布の種類:離散型と連続型
確率分布には「離散型」と「連続型」の2種類があります。
【離散型】
●事象:取りうる値がとびとび(コイントス、サイコロの目など)
●確率:縦軸の値(各値の確率(縦軸)を合計したら1となる)
【連続型】
●事象:取りうる値が連続的な値(身長・体重など)
●確率:関数(分布の曲線)の面積($${\pm\infty}$$区間で積分すると1となる)
●補足:連続型の縦軸は”確率密度”であり確率や相対度数とは異なります。
4-3.確率密度関数と確率質量関数
離散型データに対して確率をプロットした分布(関数)を「確率質量関数(pmf:probability mass function)」と呼びます。
ただ数理モデルなどでは離散値ではなく無限の値を取り得る連続値(連続確率変数)を使用します。連続値を使用する関数を「確率密度関数(PDF:probability density function」呼びます。

確率密度関数の縦軸は「確率密度」であり事象の生じやすさを表しますが確率そのものではありません。確率は確率密度関数を積分して区間内の面積から算出できます。
$$
確率密度関数f(x)
$$
$$
確率P(x≦X≦b) = \int_{a}^{b}f(x)dx (aからbの範囲に値が発生する確率)
$$
5.確率分布の紹介
確率分布の紹介と可視化を実施します。ここではPythonライブラリのScipyを使用しました。コードのベースは下記を使用して図を微調整しました。
[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import os
from scipy import stats
x = np.arange(-5, 5, 0.01)
def showGraph(x, y, label, verbose=False):
fig = plt.figure(figsize=(10, 6), facecolor='w')
ax = fig.add_subplot(111)
#確率密度分布
ax.plot(x, y, label=label)
#体裁調整
if y.max() >= 0.5:
param_ytick = 0.1
else:
param_ytick = 0.05
ax.set(xlabel='x', ylabel='確率密度f(x)',
xticks=np.arange(x.min(), x.max(), 1),
yticks=np.arange(0, y.max()+0.1, param_ytick))
plt.title(f'{label}の確率密度', y=-0.15)
plt.grid()
plt.legend()
if verbose:
if os.path.exists('image') == False:
os.mkdir('image') #imageフォルダがなければ作成
plt.savefig(f'image/確率密度_{label}.png')
plt.show()
def showGraph_mstd(x, y, mean, std, label, verbose=False):
fig = plt.figure(figsize=(10, 6), facecolor='w')
ax = fig.add_subplot(111)
#確率密度分布
ax.plot(x, y, label=label)
#平均値
_x = np.where(x <= mean)[0][-1] #平均値のxのindex
y_mean = y[_x] #平均値のy
ax.plot([mean, mean], [0, y_mean], color='red', ls='dashed', lw=1, label='平均値μ')
#標準偏差1σ
_x1_sigma1 = np.where(x <= mean-std)[0][-1] #標準偏差のxのindex
_x2_sigma1 = np.where(x >= mean+std)[0][0] #標準偏差のxのindex
ax.plot([mean-std, mean-std], [0, y[_x1_sigma1]],
color='green', ls='dashed', lw=1, label='標準偏差-σ')
ax.plot([mean+std, mean+std], [0, y[_x2_sigma1]],
color='green', ls='dashed', lw=1, label='標準偏差+σ')
#標準偏差2σ
_x1_sigma2 = np.where(x <= mean-2*std)[0][-1] #標準偏差のxのindex
_x2_sigma2 = np.where(x >= mean+2*std)[0][0] #標準偏差のxのindex
ax.plot([mean-2*std, mean-2*std], [0, y[_x1_sigma2]],
color='blue', ls='dashed', lw=1, label='標準偏差-2σ')
ax.plot([mean+2*std, mean+2*std], [0, y[_x2_sigma2]],
color='blue', ls='dashed', lw=1, label='標準偏差+2σ')
#体裁調整
if y.max() >= 0.5:
param_ytick = 0.1
else:
param_ytick = 0.05
ax.set(xlabel='x', ylabel='確率密度f(x)',
xticks=np.arange(x.min(), x.max(), 1),
yticks=np.arange(0, y.max()+0.1, param_ytick))
plt.title(f'{label}の確率密度', y=-0.15)
plt.grid()
plt.legend()
if verbose:
if os.path.exists('image') == False:
os.mkdir('image') #imageフォルダがなければ作成
plt.savefig(f'image/確率密度_{label}.png')
plt.show()
[OUT]5-1.確率分布の関係
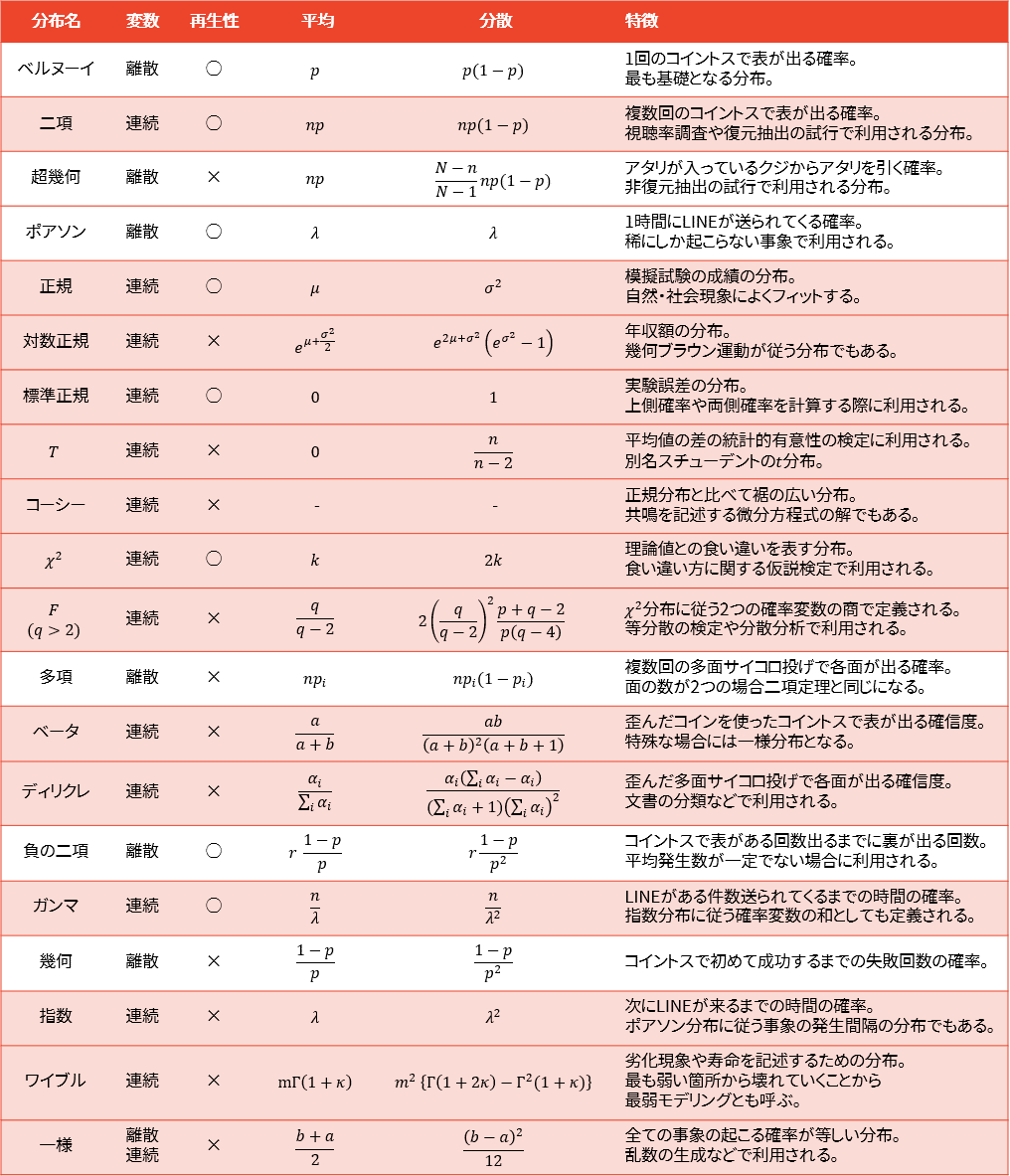
確率分布にはそれぞれに関係性があります。大きな関係性は下図の通りです(出典:【徹底解説】確率分布一覧総まとめ)。

5ー2.正規分布(ガウス分布)
正規分布(ガウス分布)の概要は下記の通りです(平均:$${\mu}$$、標準偏差:$${\sigma}$$)。
●特徴
1.平均値を中心として左右対称の釣り鐘型(Bell Curve)であり、標準偏差$${\sigma}$$間に入る確率は決まっている(例:$${\mu}$$±1.96$${\sigma}$$の範囲にデータの95%が含まれる)。
2.正規分布同士の差も正規分布となる。
●パラメータ
正規分布:平均$${\mu}$$、標準偏差$${\sigma}$$の分布
標準正規分布:平均$${0}$$、標準偏差$${1}$$
●事象例:自然現象に基づくばらつき


【正規分布の数式※表記方法が複数あるため何個か記載】
$$
正規分布:\displaystyle X\sim N(\mu ,\sigma ^{2})=\mathcal{N}(x|μ, \sigma^2)=\dfrac{1}{\sqrt{2\pi\sigma^2}}\exp(-\dfrac{(x-\mu)^ 2}{2\sigma^ 2})
$$
$$
標準正規分布f(x)=\mathcal{N}(x|0, 1)=\dfrac{1}{\sqrt{2\pi}}\exp(-\dfrac{x^ 2}{2})
$$

Pythonでの実装は下記の通りです。
[IN]
#正規分布:平均0、標準偏差1
mean, std = 0, 1
x = np.arange(-5, 5, 0.01)
y = stats.norm.pdf(x, loc=mean, scale=std)
showGraph_mstd(x, y, mean, std, '正規分布', verbose=True)
[OUT]
【コラム:正規分布を分解してみる】
下図の通り正規分布を式内の$${(x-\mu)^ 2}$$から変換して作成可能です。

上のイメージをPythonコードでも表現してみました。正規化後の分布:正規分布の面積が1であることも確認できました。
[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib
#正規分布を形状変換しながら描写
x = np.linspace(0, 10, 100)
mu, sigma = 5, 1 #平均、標準偏差
class Calc_NormDist:
def __init__(self, mu, sigma, x):
self.mu = mu #平均値
self.sigma = sigma #標準偏差
self.x = x #x軸の値
def square_curve(self, x):
return x**2 #x^2
def square_curve_slide(self, x, mu):
return (x-mu)**2 #(x-mu)^2
def square_curve_slide_scale(self, x, mu, sigma):
return -((x-mu)**2)/(2*sigma**2) #((x-mu)^2)/(2*sigma^2)
def exp_square_curve_slide_scale(self, x, mu, sigma):
return np.exp(-((x-mu)**2)/(2*sigma**2)) #exp((x-mu)^2)/(2*sigma^2)
def scaled_norm_dist(self, x, mu, sigma):
return np.exp(-((x-mu)**2)/(2*sigma**2))/(sigma*np.sqrt(2*np.pi))
def calc_integral(self, xs, yx):
total_area = 0 #積分値を格納する変数
for idx in range(len(xs)):
if idx == 0:
x, y = xs[idx], yx[idx]
continue
else:
x_next, y_next = xs[idx], yx[idx]
delta_x = x_next - x #xの変化量
y_avg = (y + y_next)/2 #yの平均値
area = delta_x * y_avg #面積
total_area += area #積分値を更新
x, y = x_next, y_next #使用した値を1つ前の値として更新
return total_area
def plot_norm_dist(ax, x, y, title):
if y.max() >= 100:
y_max = 100
elif y.max() <= 0:
y_max = 0
else:
y_max = y.max()
if y.min() > 0:
y_min = 0
else:
y_min = y.min()
sns.lineplot(x=x, y=y, ax=ax)
ax.set(xlabel='x', ylabel='y', ylim=(y_min, y_max), xticks=np.arange(x.min(), x.max()+1, 1))
ax.set_title(title, y=-0.15)
ax.grid()
#インスタンス化
normdist = Calc_NormDist(mu, sigma, x) #μ=5, σ=1の正規分布
x_square = normdist.square_curve(x) #x^2
x_square_slide = normdist.square_curve_slide(x, mu) #(x-mu)^2
x_square_slide_scale = normdist.square_curve_slide_scale(x, mu, sigma) #((x-mu)^2)/(2*sigma^2)
epx_x_square_slide_scale = normdist.exp_square_curve_slide_scale(x, mu, sigma) #exp((x-mu)^2)/(2*sigma^2)
norm_distribution = normdist.scaled_norm_dist(x, mu, sigma) #正規分布
fig, axs = plt.subplots(3, 2, figsize=(10, 18))
axs = axs.flatten()
plot_norm_dist(axs[0], np.linspace(-5, 5, 100), np.exp(np.linspace(-5, 5, 100)), r'f(x)=$\exp(x)$')
plot_norm_dist(axs[1], x, x_square, r'f(x)=$x^2$')
plot_norm_dist(axs[2], x, x_square_slide, r'f(x)=$(x-\mu)^2$$\to \mu$だけスライド')
plot_norm_dist(axs[3], x, x_square_slide_scale, r'f(x)=$-\frac{(x-\mu)^2}{2\sigma^2} \to$ 符号反転+スケーリング')
plot_norm_dist(axs[4], x, epx_x_square_slide_scale, r'f(x)=$\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) \to$指数関数化$\to$Max=1~Min=0の分布')
plot_norm_dist(axs[5], x, norm_distribution, r'f(x)=$\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$ 正規分布')
#面積確認
print(f'正規化前の面積:{normdist.calc_integral(x, x_square):.3f}')
print(f'正規分布の面積:{normdist.calc_integral(x, norm_distribution):.3f}')
[OUT]
正規化前の面積:333.350
正規分布の面積:1.000
5-2-1.多次元正規分布(多変量ガウス分布)
正規分布は多次元(ベクトルの正規分布)でも作成可能です。

$$
p(x)=f(x;μ,Σ) = \frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)
$$
$${\boldsymbol{x}}$$:確率変数の$${n}$$次元のベクトル
$${\boldsymbol{\mu}}$$:平均値を表す$${n}$$次元のベクトル
$${\boldsymbol{\Sigma}}$$:共分散行列を表す$${n\times n}$$行列
$${\boldsymbol{\Sigma}^{-1}}$$:共分散行列の逆行列
$${(\boldsymbol{x}-\boldsymbol{\mu})^{\mathrm{T}}}$$:$${\boldsymbol{x}-\boldsymbol{\mu}}$$の転置
[IN]
from scipy.stats import norm
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Create grid of x, y values
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
x, y = np.meshgrid(x, y)
# Compute z values as the normal pdf
z = norm.pdf(np.sqrt(x**2 + y**2)) #標準正規分布の確率密度関数
#統計量確認
print(f'x 平均値: {x.mean():.3f}, 標準偏差: {x.std():.3f}, 最大値: {x.max():.3f}, 最小値: {x.min():.3f}')
print(f'y 平均値: {y.mean():.3f}, 標準偏差: {y.std():.3f}, 最大値: {y.max():.3f}, 最小値: {y.min():.3f}')
print(f'z 平均値: {z.mean():.3f}, 標準偏差: {z.std():.3f}, 最大値: {z.max():.3f}, 最小値: {z.min():.3f}')
#共分散行列を計算
cov = np.cov(x.flatten(), y.flatten())
print(f'共分散行列:\n {cov}')
# 3D plot
# Create 3D plot
fig = plt.figure(figsize=(12,5),facecolor='w', edgecolor='k')
ax = fig.add_subplot(111, projection='3d')
surf = ax.plot_surface(x, y, z, cmap='jet') #3Dプロットを作成
fig.colorbar(surf) #カラーバーを表示
ax.set_xlabel('X'), ax.set_ylabel('Y'), ax.set_zlabel('Z') #ラベルを表示
ax.set_title("3次元正規分布") #タイトルを表示
plt.show()
fig, axs = plt.subplots(1, 2, figsize=(12, 5), facecolor='w', edgecolor='k')
# Contour plot
im = axs[0].contourf(x, y, z, cmap='jet') #等高線を表示
axs[0].set_xlabel('X'), axs[0].set_ylabel('Y') #ラベルを表示
axs[0].set_title("3次元正規分布を2次元に投影(x-y平面)") #タイトルを表示
plt.colorbar(im,ax=axs[0]) #カラーバーを表示
# Line plot
axs[1].plot(x, z)
axs[1].set_xlabel('X')
axs[1].set_ylabel('Z')
axs[1].set_title("3次元正規分布を2次元に投影(x-z平面)")
plt.show()
[OUT]
x 平均値: 0.000, 標準偏差: 1.749, 最大値: 3.000, 最小値: -3.000
y 平均値: 0.000, 標準偏差: 1.749, 最大値: 3.000, 最小値: -3.000
z 平均値: 0.068, 標準偏差: 0.095, 最大値: 0.399, 最小値: 0.000
共分散行列:
[[3.06091215e+00 1.49228897e-17]
[1.49228897e-17 3.06091215e+00]]

5ー2-2.対数正規分布
対数正規分布の概要は下記の通りです。
特徴:左右対称ではなく裾が重い分布となる。
パラメータ:平均$${\mu}$$、標準偏差$${\sigma}$$
事象例:所得分布など
$$
f(x) = \frac{1}{\sqrt{2\pi\sigma^{2}}x} \exp \left( -\frac{(\ln x – \mu)^{2}}{2\sigma^{2}} \right) \ ,
$$
5ー2-3.適用例:ガウジアンノイズ/フィルタ
正規分布の適用例としては「ガウジアンノイズ」や「ガウジアンフィルタ」があります。
【ガウジアンノイズ】
ガウジアンノイズとは各ピクセルごとに正規分布に従う偏差σ(20〜40)で乱数をふり輝度を変更する手法です。画像でノイズを加える時などに使用されます(AIではノイズを加えることでロバスト性を高めます)。
【ガウジアンフィルタ】
画像のフィルター処理の1つで「対象とする画素に近いほど大きい重みを付与できるように重みを設定したフィルタ」です。
平滑化(ぼかし)の機能もありますが”ガウジアンフィルタによるノイズ除去”の機能もあるみたいです。

$$
h_g=\frac{ 1 }{ 2\pi\sigma^2 }\exp{(-\frac{x^2+y^2}{2\sigma^2})}
$$
[IN]
import numpy as np
import numpy as np
import pandas as pd
def gaussian_filter(size, sigma):
x, y = np.mgrid[-size:size+1, -size:size+1]
g = 1/(2*np.pi * sigma**2)*np.exp(-(x**2 + y**2) / (2 * sigma**2))
return g/g.sum()
gaussian_kernel = gaussian_filter(size=5, sigma=5.0)
import matplotlib.pyplot as plt
plt.imshow(gaussian_kernel, cmap='jet')
plt.title('2D Gaussian filter')
plt.colorbar()
plt.show()
pd.DataFrame(gaussian_kernel).style.background_gradient(cmap='gray')
[OUT]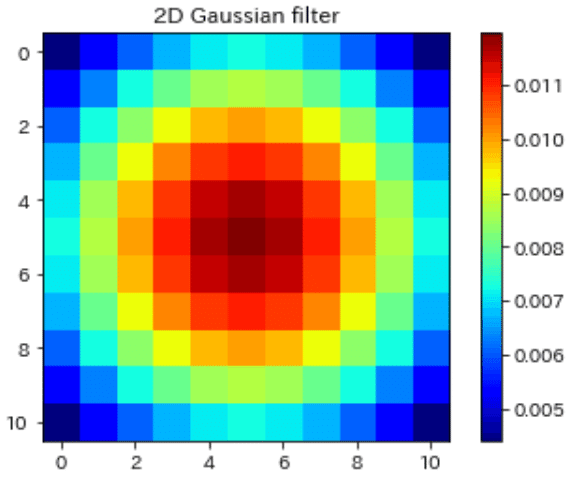

5-2-4.製造の品質管理:シックスシグマ
製造業において製品の品質(基準値)は必ずばらつきが発生し、ばらつきが大きいと不良品が発生するため無駄なコストが発生します。ばらつきの要因に直接的な因果関係がない場合、このばらつき(つまり標準偏差$${\sigma}$$)は正規分布に従います。
例えば不良品を5%以下にしたい場合はばらつきを±1.96$${\sigma}$$に抑える必要があります。製品品質を±6$${\sigma}$$内に収める管理手法をシックスシグマと呼びます。

なおシックスシグマを導入有無に限らず重要なのは「品質管理基準を保つためにばらつきが生じる原因をつぶして対策すること」です。これは用語を知っているだけでは意味がなく地道な改善が重要となります。
5ー3.べき分布
べき分布(power law distribution)の概要は下記の通りです。
特徴:中央値や最頻値の分布が左端に位置し、右に行くほどべき乗で減衰していく。平均値や分散の値に意味はない。東京電力福島第一原発のように影響が大きいリスクがある場合は確率が低くても無視できないためロングテール側の確率も考慮する必要がある。
パラメータ:分散は無限大(スケールフリー)
事象例:地震のマグニチュードに対する発生頻度
$$
べき分布p(x) = Cx^{-\alpha}
$$
Pythonでは「Scipyのscipy.stats.expon」を使用します。
[IN]
#べき分布
y = stats.expon.pdf(x, loc=0, scale=1)
showGraph(x, y, 'べき分布', verbose=True)
[OUT]
5ー4.ベルヌーイ分布
ベルヌーイ分布 (Bernoulli distribution)の概要は下記の通りです。
●特徴
ある確率で2値《正例/負例(1/0)》をとる離散分布
試行結果が0と1の2種類のみの確率実験はベルヌーイ試行と呼ばれる。
●パラメータ
成功確率:p、平均:p、分散:p-1
分散:偏差(平均との差)の2乗の期待値であり「xの2乗の平均」と「xの平均の2乗」との差が分散となる
●事象例:コイントス、消費者の購買確率
$$
成功確率P(X=1)=p
$$
$$
失敗確率P(X=0)=1−p
$$
$$
\begin{aligned}
期待値E(X)
=\sum_{x=0}^{1}xP(X=x)\\
=1\times p+0\times(1-p)=p
\end{aligned}
$$
分散の計算では上記で求めた期待値$${E(X)=p}$$より$${E(X)^2=p^2}$$、期待値の定数は定数自体になる$${E(a)=a}$$、期待値の線型性(線形性)、期待値内の定数は変数の前に出せる性質を利用して変換することで導出可能です。
$$
期待値の線型性:E(aX+bY)=E(aX)+E(bY)=aE(X)+bE(Y)
$$
$$
\begin{aligned}
分散V(X)= E[(X-E(X))^2] \\
=E[X^2 - 2XE[X] + (E[X])^2]\\
=E[X^2] - E[2XE[X]] + E[(E[X])^2\\
=E[X^2] - 2E[X]E[X] + (E[X])^2\\
=E[X^2] - (E[X])^2\\
=\sum_{k} P(X=x) \cdot x^2- (E[X])^2\\
=(P(X=0) \cdot 0^2 + P(X=1) \cdot 1^2)- (E[X])^2\\
=((1-p) \cdot 0 + p \cdot 1)- (E[X])^2\\
=p-(p^2)\\
=p(1-p)
\end{aligned}
$$
$$
標準偏差\sigma=\sqrt{V(X)}=\sqrt{p(1-p)}
$$
ベルヌーイ試行をPythonで実装しました。理論確率は$${\frac{1}{2}}$$としておりますが、(特に低試行回数n時では)ランダムのため得られる結果は$${\frac{1}{2}}$$にはなりませんでした。
なお大数の法則より、試行回数を増やすと確率は真値$${\frac{1}{2}}$$に近づいていることが確認できます。
[IN]
np.random.seed(0)
#ベルヌーイ分布
prop = 0.5 #真値(表)の確率
props = (prop, 1-prop) #表、裏の確率
coins_5 = np.random.choice([0, 1], size=5, p=props)
coins_10 = np.random.choice([0, 1], size=10, p=props)
coins_50 = np.random.choice([0, 1], size=50, p=props)
coins_1000 = np.random.choice([0, 1], size=1000, p=props)
print(coins_5)
print(f'表0の数:{np.sum(coins_5==0)}, 裏1の数:{np.sum(coins_5==1)}')
#可視化
plt.rcParams['font.size'] = 12
fig, axs = plt.subplots(2, 2, figsize=(18, 10), facecolor='w')
#サンプルサイズ5
axs[0][0].bar([0, 1], [np.sum(coins_5==0), np.sum(coins_5==1)],
tick_label=['表:0', '裏:1'], ec='k', color=['r', 'b'])
axs[0][0].plot([0, 1], np.array([prop, prop])*len(coins_5), ls='dashed', c='gray', lw=1)
axs[0][0].set(title='Sample size=5', ylabel='出現回数')
#サンプルサイズ10
axs[0][1].bar([0, 1], [np.sum(coins_10==0), np.sum(coins_10==1)],
tick_label=['表:0', '裏:1'], ec='k', color=['r', 'b'])
axs[0][1].plot([0, 1], np.array([prop, prop])*len(coins_10), ls='dashed', c='gray', lw=1)
axs[0][1].set(title='Sample size=10', ylabel='出現回数')
#サンプルサイズ50
axs[1][0].bar([0, 1], [np.sum(coins_50==0), np.sum(coins_50==1)],
tick_label=['表:0', '裏:1'], ec='k', color=['r', 'b'])
axs[1][0].plot([0, 1], np.array([prop, prop])*len(coins_50), ls='dashed', c='gray', lw=1)
axs[1][0].set(title='Sample size=50', ylabel='出現回数')
#サンプルサイズ1000
axs[1][1].bar([0, 1], [np.sum(coins_1000==0), np.sum(coins_1000==1)],
tick_label=['表:0', '裏:1'], ec='k', color=['r', 'b'])
axs[1][1].plot([0, 1], np.array([prop, prop])*len(coins_1000), ls='dashed', c='gray', lw=1)
axs[1][1].set(title='Sample size=1000', ylabel='出現回数')
[OUT]
[1 1 1 1 0]
表0の数:1, 裏1の数:4
5ー5.二項分布
二項分布の概要は下記の通りです。
特徴:ベルヌーイ試行をn回行った場合にその成功回数が従う確率分布
パラメータ:試行回数:n、成功確率:p、平均:np、分散:np(1-p)
事象例:コイントス、消費者の購買確率
$$
二項分布P(X=k)={}_nC_k p^ k(1-p)^{n-k}
$$
$$
組み合わせ_nC_r=\dfrac{n!}{r!(n-r)!}
$$
二項分布とベルヌーイ分布の比較表は下記の通りです。

5-5-1.Python実装
Pythonでは「Scipyのscipy.stats.binom」を使用します。
[IN]
prob = 0.5 #確率p
n1, n2, n3, n4= 3, 10, 30, 100 #試行回数n
#試行回数中の表が出る回数(0~n+1)
x1, x2, x3, x4 = np.arange(n1+1), np.arange(n2+1), np.arange(n3+1), np.arange(n4+1)
#二項分布
y1, y2, y3, y4 = stats.binom.pmf(x1, n1, p), stats.binom.pmf(x2, n2, p), stats.binom.pmf(x3, n3, p), stats.binom.pmf(x4, n4, p)
#可視化
plt.rcParams['font.size'] = 11
fig, axs = plt.subplots(2, 2, figsize=(18, 12), facecolor='w')
#試行回数3
axs[0][0].bar(x1, y1, ec='k', color='b')
axs[0][0].set(title=f'試行回数={n1}', ylabel='確率', xlabel='表が出る回数', xticks=x1)
#試行回数10
axs[0][1].bar(x2, y2, ec='k', color='b')
axs[0][1].set(title=f'試行回数={n2}', ylabel='確率', xlabel='表が出る回数', xticks=x2)
#試行回数30
axs[1][0].bar(x3, y3, ec='k', color='b')
axs[1][0].set(title=f'試行回数={n3}', ylabel='確率', xlabel='表が出る回数', xticks=x3)
#試行回数100
axs[1][1].bar(x4, y4, ec='k', color='b')
axs[1][1].set(title=f'試行回数={n4}', ylabel='確率', xlabel='表が出る回数')
plt.show()
[OUT]
5-5-2.コイントスでの分布シミュレーション
コイントスを実施した時に二項分布に従うことを検証してみました。条件は下記の通りです。
事象:表(0)と裏(1)
表の出る確率p:0.5、裏が出る確率=1-p=0.5
サンプルサイズ(コイントスの回数):n
試行回数(サンプル数):n回のコイントスを1試験としたときの試験数
まずはコイントスをするクラスと可視化の関数を作成しました。可視化時には赤線で二項分布の理論値をプロットするようにしています。
なおxtickとytickは各グラフで手動で微調整しております。
[IN]
class ThrowCoin:
def __init__(self, prob, sample_size):
self.p_front = prob #真値(表)の確率
self.p_back = 1 - prob #真値(裏)の確率
self.values = (0, 1) #表、裏の値
self.sample_size = sample_size
self.s_index = np.arange(0, sample_size+1, 1)
self.output = np.zeros(sample_size+1)
def __call__(self, iteration):
for _ in range(iteration):
result = np.random.choice(self.values,
size=self.sample_size,
p=(self.p_front, self.p_back))
num_True = np.sum(result==1) #正例の数
idx = self.s_index[self.s_index==num_True] #正例の数に対応するインデックス
self.output[idx] += 1 #インデックスの値を1増やす
return self.output
def showGraph_Bi(x, y, prob, sample_size, iteration, verbose=False):
plt.rcParams['font.size'] = 12
#二項分布のグラフ(理論値)
prob_binom = stats.binom.pmf(x, sample_size, prob)
value_binom = prob_binom * iteration
fig, ax = plt.subplots(figsize=(12, 6), facecolor='w')
ax.bar(x, y, ec='w', label='実験値')
ax.plot(x, value_binom, c='red', lw=1, label='二項分布')
ax.set(xlabel='表が出た回数', ylabel='発生回数',
xticks=np.arange(0, np.array(x).max()+1, 1),
yticks=np.arange(0, np.array(y).max()+1, iteration//50+1))
plt.title(f'{sample_size}回コイントスを{iteration}回実施した時の表の出現率', y=-0.18)
plt.grid(), plt.legend()
if verbose:
plt.savefig(f'image/coin_{sample_size}_{iteration}.png')
plt.show()
[OUT]初めにコイントス数n=1での試験を1回だけ実施した時の結果を確認します。結果は裏か表のどちらかであり、表の出る回数は0か1となります。今回はたまたま表が出ました。
[IN]
prob = 0.5 #正例(表)の確率
sample_size = 1 #サンプルサイズ
iteration = 1 #試行回数n
coins = ThrowCoin(prob, sample_size)
x = np.arange(0, sample_size+1, 1)
y = coins(iteration)
print(y)
showGraph_Bi(x, y, prob, sample_size, iteration, verbose=True)
[OUT]
[0. 1.]
次にコイントス数n=5, サンプル数10で試験しました。今回は「5回投げて3回表が出る回数が最も多く、4回表が出る回数は0回」となりました。
[IN]
prob = 0.5 #正例(表)の確率
sample_size = 5 #サンプルサイズ
iteration = 10 #試行回数n
coins = ThrowCoin(prob, sample_size)
x = np.arange(0, sample_size+1, 1)
y = coins(iteration)
print(y)
showGraph_Bi(x, y, prob, sample_size, iteration, verbose=True)
[OUT]
[1. 2. 2. 4. 0. 1.]
次に分布を幅広くするためにコイントス数n=100と大きくして、分布が理論値に近づくように試行回数も大きく(1万回)にしました。結果としてはかなり二項分布に近づいていることが確認できます。
[IN]
prob = 0.5 #正例(表)の確率
sample_size = 100 #サンプルサイズ
iteration = 10000 #試行回数n
coins = ThrowCoin(prob, sample_size)
x = np.arange(0, sample_size+1, 1)
y = coins(iteration)
print(y)
showGraph_Bi(x, y, prob, sample_size, iteration, verbose=True)
[OUT]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
1. 1. 2. 0. 1. 2. 5. 14. 16. 33. 38. 73. 121. 162.
214. 308. 404. 462. 611. 638. 689. 785. 765. 790. 761. 688. 590. 459.
371. 294. 275. 151. 101. 70. 37. 31. 14. 11. 8. 0. 2. 0.
1. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0.]
5-5-3.事例で確認:商品の抜き取り検査
不良品(正例)がpの確率で発生する工場で抜き取り検査をします。n個抜き出す時に不良品がk個得られる可能性を計算します。
例として抜き出し数n=5, 10において、p=0.05~0.25(不良品発生率5~25%)での不良品発生数kを出力しました。
[IN]
#Pandasの小数点以下第3位まで表示
pd.options.display.float_format = '{:.3f}'.format
class HorizontalDisplay:
def __init__(self, *args):
self.args = args
def _repr_html_(self):
template = '<div style="float: left; padding: 10px;">{}</div>'
return ''.join(template.format(a._repr_html_()) for a in self.args)
def inspect_binom(n, probs):
x = np.arange(n+1) #検査で正例になる回数
ps, nums_True = np.meshgrid(probs, x) #正例になる回数と確率の組み合わせ
y = stats.binom.pmf(nums_True, n, ps) #正例の確率pと正例の数の組み合わせに対する確率
cols = [f'p={p}' for p in probs]
df = pd.DataFrame(y, index=x, columns=cols)
df.rename_axis('正例の数k', axis=0, inplace=True) #indexの名前を変更
return df
n5, n10 = 5, 10 #試行回数
probs = [0.05, 0.1, 0.15, 0.2, 0.25] #確率p
df_n5 = inspect_binom(n5, probs)
df_n10 = inspect_binom(n10, probs)
display(HorizontalDisplay(df_n5, df_n10))
def show_binomGraph(df, verbose=False):
n = df.index[-1]
cols = df.columns
fig = plt.figure(figsize=(10, 5), facecolor='w')
ax = fig.add_subplot(111)
for col in cols:
ax.plot(df.index, df[col], label=col)
ax.set(title=f'試行回数={df.index[-1]}', xlabel='正例(不良品)の取得確率', ylabel='確率p',
yticks=np.arange(0, 1.1, 0.1))
plt.legend(), plt.grid()
if verbose:
if os.path.exists('image') == False:
os.mkdir('image')
plt.savefig(f'image/二項分布(不良品検査)_試行回数{n}.png')
plt.show()
show_binomGraph(df_n5, verbose=True)
[OUT]
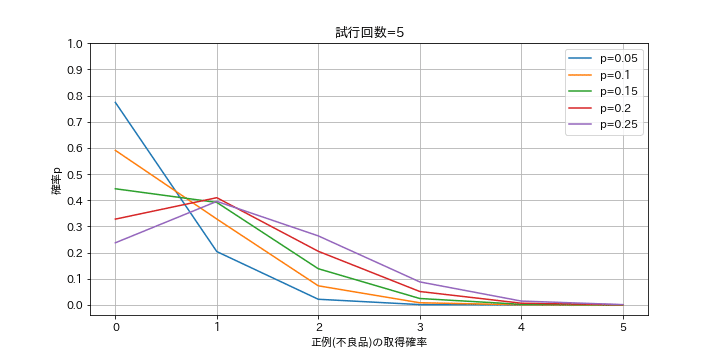
結果として抜き取り数n=5, 不良品発生率p=5%での不良品が出ない(k=0)確率は77.4%です。抜き取り数をn=5->10に増やすとk=0は59.9%、抜き取り数n=5として発生率p=5->25%に増やすとk=0は23.7%に減少しました。
5ー6.ポアソン分布
ポアソン分布の概要は下記の通りです。なおポアソン分布は二項分布の拡張版みたいなものになります。
特徴:滅多には起こらないが必ず起こる事象について、ある特定期間で何回起こるかを表す確率分布。$${\lambda}$$が大きくなるにつれて正規分布に近づきます。
パラメータ:期待発生回数$${\lambda}$$、平均:$${\lambda}$$、分散:$${\lambda}$$
事象例:飛行機事故など
$$
ポアソン分布P(X=k)=\dfrac{\lambda^ k e^{-\lambda}}{k!}
$$
Pythonでは「Scipyのscipy.stats.poisson」を使用します。事例として「(あまり発生しない)不良品の発生率」で確認します。
抜き出し数n=10、不良品発生率p=0.5%(200個に1個)の場合の不良品発生率をPythonで実装します。パラメータの期待発生回数$${\lambda=n \times p}$$で計算します。
[IN]
#ポアソン分布
x = np.arange(10) #正例になる回数
n = 10 #抜き取り検査数
p = 1/200 #不良品の確率 0.5%
p_ave = n*p #期待発生確率λ
y = stats.poisson.pmf(x, p_ave)
df = pd.DataFrame(y, index=x, columns=['確率'], dtype='float64').rename_axis('正例の数k', axis=0)
display(df.T)
showGraph(x, y, label='ポアソン分布', verbose=True)
[OUT]

上記より、10個抜き出して不良品が1個検出される確率は4.8%、2個検出は0.1%であることが計算できます。つまりバッチ数(ロット数)が10個/batchの製品があり99.9%の検出をしたいのであれば(全数ではなく)2個抜出検査すればよいと判断できます。
参考として、不良品検出数k=1個の計算値は下記の通りです。
$$
P(X=1)=\dfrac{\lambda^ k e^{-\lambda}}{k!}=\dfrac{\lambda^{1} e^{-0.05}}{1!}=0.048
$$
5ー7.カイ二乗分布
$${\chi^2}$$分布の概要は下記の通りです。
●特徴:標準分散が従う分布であり、母集団の分散を推定できる。自由度kに従い分布が変わる。
●パラメータ:ー
●事象例:ー
結果で出る期待値と現実に起こる結果の食い違い度合の分布
$$
\chi^2分布f(x;k)=\dfrac{1}{2^{k/2}\Gamma (k/2)}x^{k/2-1}e^{-x/2}
$$
5-7-1.数式詳細
Zが標準正規分布に従うとき下記式に従う分布が$${\chi^2}$$分布である。
$$
\chi^2 = Z_{1}^2 + Z_{2}^2 + \cdots + Z_{n}^2 (k:自由度)
$$
$$
= (\frac{x_{1}-\mu}{\sigma})^2 + (\frac{x_{2}-\mu}{\sigma})^2 + \cdots + (\frac{x_{n}-\mu}{\sigma})^2
$$
母集団が正規分布に従うとしても、実際には母集団の平均値$${\mu_p}$$や標準偏差$${\sigma_p}$$はわからないため、標本平均$${\overline X}$$で代用します。この時自由度k=n-1の$${\chi^2}$$分布に従います。
$$
= (\frac{x_{1}-\overline X}{\sigma})^2 + (\frac{x_{2}-\overline X}{\sigma})^2 + \cdots + (\frac{x_{n}-\overline X}{\sigma})^2
$$
5-7-2.Pythonの実装
[IN]
# カイ二乗分布
x = np.arange(0.01, 10, 0.01)
d_free1, d_free2, d_free3, d_free5, d_free10 = 1, 2, 3, 5, 10
chi_df1 = stats.chi2.pdf(x, d_free1)
chi_df2 = stats.chi2.pdf(x, d_free2)
chi_df3 = stats.chi2.pdf(x, d_free3)
chi_df5 = stats.chi2.pdf(x, d_free5)
chi_df10 = stats.chi2.pdf(x, d_free10)
fig = plt.figure(figsize=(10, 6), facecolor='w')
ax = fig.add_subplot(111)
#確率密度分布
ax.plot(x, chi_df1, label='自由度k=1')
ax.plot(x, chi_df2, label='自由度k=2')
ax.plot(x, chi_df3, label='自由度k=3')
ax.plot(x, chi_df5, label='自由度k=5')
ax.plot(x, chi_df10, label='自由度k=10')
ax.set(xlabel='x', ylabel='確率密度f(x)',
xticks=np.arange(0, x.max(), 1),
yticks=np.arange(0, 1.1, 0.1),
ylim=(0, 1))
plt.title(f'カイ2乗分布の確率密度', y=-0.15)
plt.grid()
plt.legend()
plt.show()
[OUT]
5ー8.スチューデントの t 分布
t分布(スチューデントのt)の概要は下記の通りです。
●特徴:標本平均を「標本から得た標準偏差」で準標準化した統計量 T は t 分布に従うことが分かっている
ー>少ないサンプル数から母集団の平均を推定できる。
ー>自由度(標本数)が大きくなるほど分布のばらつきが小さくなるため、推定精度が上がる
●パラメータ:自由度=標本数n-1
●事象例:ー
$$
f(x) = \frac{\Gamma \left( \frac{m_1 + m_2}{2}\right)}
{\sqrt{m\pi} \Gamma \left( \frac{m}{2} \right)
\left( 1+ \frac{x^2}{m} \right)^{\frac{m+1}{2}}}
\hspace{20px} (-\infty<x<\infty)
$$
各自由度におけるt分布の変化は下図の通りです。
[IN]
#t分布
num_sample1, num_sample2, num_sample3, num_sample4 = 2, 6, 11, 21 #標本数
d_free1, d_free2, d_free3, d_free4 = num_sample1-1, num_sample2-1, num_sample3-1, num_sample4-1 #自由度
x = np.arange(-4, 4, 0.01) #x軸の範囲
y_norm = stats.norm.pdf(x) #正規分布の確率密度関数
y1 = stats.t.pdf(x, d_free1) #t分布の確率密度関数
y2 = stats.t.pdf(x, d_free2) #t分布の確率密度関数
y3 = stats.t.pdf(x, d_free3) #t分布の確率密度関数
y4 = stats.t.pdf(x, d_free4) #t分布の確率密度関数
fig, ax = plt.subplots(1, 1, figsize=(12, 6), facecolor='w')
ys = [y_norm, y1, y2, y3, y4]
for idx, y in enumerate(ys):
if idx == 0:
ax.plot(x, y, label='正規分布', ls='--', color='black')
ax.plot(x, y, label=f't分布(自由度={idx})')
idx += 1
ax.set(title='t分布', xlabel='x', ylabel='確率密度関数')
plt.legend(), plt.grid()
plt.show()
[OUT]
各自由度におけるt分布の確率、t値は下記の通りです。
[IN]
pd.options.display.float_format = '{:.3f}'.format #小数点以下3桁表示
#信頼区間からt分布の下側2.5%点と上側2.5%点を求める
t_low = stats.t.ppf(0.025, 5) #t分布の下側2.5%点
t_upper = stats.t.ppf(0.975, 5) #t分布の上側2.5%点
print(f'自由度5のt分布 下型2.5%点={t_low:.3f}, 上側2.5%点={t_upper:.3f}')
#t値からt分布の面積を求める
p_1side_t1 = stats.t.cdf(-1, 5) #t分布の下側2.5%点の面積
p_both_t1 = stats.t.cdf(-1, 5)*2 #t分布の上側2.5%点の面積
print(f'自由度5のt分布 下側2.5%点の面積={p_1side_t1:.3f}, 両側2.5%点の面積={p_both_t1:.3f}')
#信頼区間(両側の面積)
ci = np.array([0.90, 0.95, 0.98, 0.99]) #信頼係数
d_frees = np.arange(1,31,1) #自由度
#信頼区間を片側の数値に変更
ci_oneside = ci + (1-ci)/2
ci_mesh, d_free_mesh = np.meshgrid(ci_oneside, d_frees)
t_value = stats.t.ppf(ci_mesh, d_free_mesh) #t分布の片側
df = pd.DataFrame(t_value,
index=d_frees,
columns=[f'p={p}(両側)' for p in ci],
dtype='float64').rename_axis('自由度', axis=0)
df
[OUT]
自由度5のt分布 下型2.5%点=-2.571, 上側2.5%点=2.571
自由度5のt分布 下側2.5%点の面積=0.182, 両側2.5%点の面積=0.363
キーワード一覧
カール・ピアソンの確率分布:ピアソンの論文 「進化の数学理論への貢献1)」で紹介された確率分布
推測統計:母集団から抽出した標本の情報を用いて、母集団の情報を推測する。統計学的に推測するには、データに当てはまるであろう確率分布を推定し、その確率分布を基に、母集団のデータを推測します。
大数の法則(law of large numbers):ある独立した試行においてその事象が発生する確率をpとすると、試行回数nが大きくなるにつれて事象の発生確率がpに近づいていくこと
中心極限定理:母集団が正規分布でなくても、そこから抽出したサンプルサイズNが大きくなると標本の分布は正規分布に近づく
モンテカルロ法:、乱数を用いた試行を繰り返すことにより近似解を求める手法->大数の法則を考慮すると試行回数nを大きくして近似解を取得
点推定/区間推定:点推定は母集団の平均や分散などの特性値を1つの値で推定し、区間推定は母集団が正規分布に従うと仮定できる場合に標本のデータを用いて母平均などの推定量を1つの値ではなく入る区間(幅)で推定します
標準誤差(SE:standard error):標本から測定された統計量の標準偏差であり標本統計量の精度を表す。標本平均の標準偏差を指すことが多い。
$$
不偏分散\sigma^2 = \frac{1}{n-1}\sum_{i=1}^{n} (x_i - \bar{x})^2
$$
$$
標準偏差\sigma = \sqrt{\sigma^2}
$$
$$
SE = \frac{\sigma}{\sqrt{n}}= \frac{\sqrt{不偏分散\sigma^2}}{\sqrt{n}}= \frac{\sqrt{\frac{1}{n-1} \displaystyle\sum^{n}_{i=1} (x_{i} - \bar{x})^{2}}} {\sqrt{n}}
$$
参考資料
技術関係
http://ankokudan.org/d/dl/pdf/pdf-kakuritu.pdf
筑波大が無料公開している初等確率論のコース。予備校の授業っぽい感じで数式展開の説明もわかりやすいhttps://t.co/CWTGy3QjF3
— QDくん⚡️Python x 機械学習 x 金融工学 (@developer_quant) January 9, 2023
確率変数と分布関数
期待値と積率
積率母関数
確率変数の変数変換
同時確率,周辺確率,条件付確率
共分散と相関係数
和の分布
基本的な確率分布
大数の法則
中心極限定理 pic.twitter.com/gX2t3Pvrty
Python
データ用
https://dashboard.e-stat.go.jp/

あとがき
追って追記予定
