Pythonライブラリ(数式処理)：SymPy

2022年12月11日 15:01

１．概要

　記号計算／数式処理（symbolic mathematics／computer algebra system）を扱うSymPyを紹介します。
　なお「弘前大学大学院理工学研究科：SymPy による数式処理とグラフ作成」を一度目に通しておくとより理解が深まります。

１－１．環境構築

　公式ではAnacondaを推奨しており、実行環境で使用しているのであれば環境構築は不要です。Anacondaのインストール方法は下記に記載してます。

　別環境でインストールする方は下記公式をご確認ください。

２．Sympyの基本操作：各種変数の定義

　まずはSymPyで使用する基本的な操作を学びます。各コードでも記載しますが、Sympyでは最初に下記2行(インポートと初期化）を実行します。
　またSympyとの相性がよいNumpyもインポートしておきます。

[IN]
import numpy as np

import sympy as sp
sp.init_printing() #LaTeX形式で出力

２－１．変数の定義：シンボル作成

　数値処理をするための変数を定義します。SympyではSymbolという形で格納され出力時には設定した形で出力されます。
　本節では１個ずつとまとめて定義する方法を紹介します。

　２－１－１．１つだけ定義：Symbol

　変数を１個だけ定義するには"sympy.Symbol('<変数名>')"を使用します。Pythonの変数に入れると出力時に定義した変数名が出力されます。

【引数】
●real{defalut:False}：True->求める解は実数のみ（虚数はなし）
●positive{defalut:False}：True->求める解は正の値のみ

[IN]
import sympy as sp
sp.init_printing() #LaTeX形式で出力

x = sp.Symbol('x') #変数xを定義
a = sp.Symbol('AAA') #変数yを定義

display(x)
display(a)

[OUT]
x
AAA

　２－１－２．まとめて定義：symbols

　複数の変数をまとめて定義するには"sympy.symbols('<変数1>' '<変数2> ・・・ '<変数n>' )"のように半角スペースで区切って変数名を記載します。

[IN]
x, y, z = sp.symbols('x y zzz') #変数x, y, zを定義
display(x, y, z)

[OUT]
x
y
zzz

　同じ記号の連番を作成する場合は"<記号><開始index>:<終了index+1>" で作成できます。

[IN]
A = sp.symbols('A1:4') #変数A1, A2, A3を定義
A

[OUT]
(A1, A2, A3)

　上記の通りsymbols内の変数を複数にして格納する変数が1つの場合はTuple型で出力されます。

[IN]
X = sp.symbols('x y zzz') #変数x, y, zを定義
print(type(X))
display(X)

[OUT]
<class 'tuple'>
(x, y, zzz)

　２－１－３．練習：LaTexによる表示

　参考までにSymbol内の記法をLateX形式で記載することが出来ます。

【Case1：上付き・下付きの記法】
　下記の通り下付きは何パターンか記法があります。

[IN]
x_upper = sp.Symbol('x^2')
display(x_upper)

x1, x2, x3 = sp.symbols('x0 x_0 x_{0}')

x1, x2, x3

[OUT]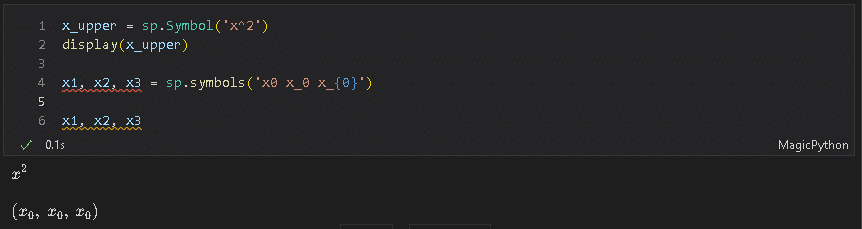

　下付きにする文字を明確にするためにはLaTex記法の方がよさそうです。

[IN]
C1, C2, C3 = sp.Symbol('CA0'), sp.Symbol('C_{A0}'), sp.Symbol('C_{A0}^*')
C1, C2, C3

[OUT]

【Case２：f-stringで記載】
　f-stringを使ったSymbolの作成もできます。

[IN]
a= 100
xa = sp.Symbol(f'x{a}')
xa

[OUT]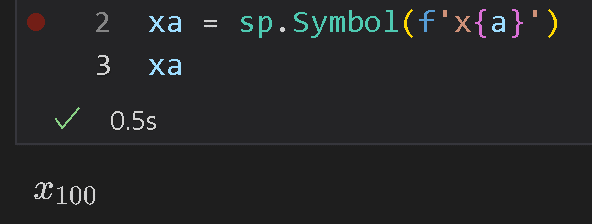

【Case３：化学式で記載】
　化学反応式もきれいに書くことができます。

[IN]
S_CH4 = sp.Symbol('CH_{4}') #Methane
S_O2 = sp.Symbol('O_{2}') #Oxygen
S_C2H4 = sp.Symbol('C_{2}H_{4}') #Ethylene
S_H2O = sp.Symbol('H_{2}O') #Water

sp.Eq(S_CH4 + 2*S_O2, S_C2H4 + 2*S_H2O) #反応式の定義

[OUT]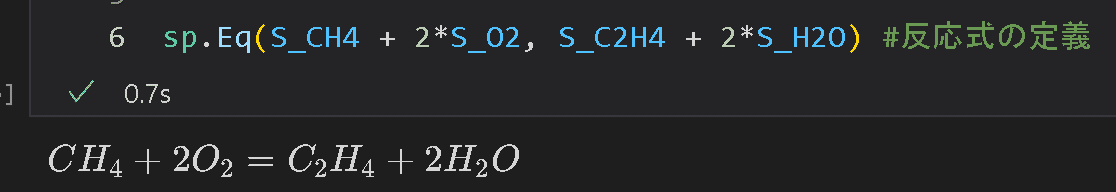

２－２．LaTeX版で表示：init_printing

　LaTex版の数式表示にしたい場合は"init_printing()"を使用します。ON/OFFは引数にBool型を渡せば切り替え可能です。
　一般的にはSympyのimportと合わせて"init_printing()"を記載します。

[IN]
sp.init_printing(False)
x = sp.Symbol('x') #変数xを定義
display(2*x**2 + 3*x + 1)
sp.init_printing(True)
display(2*x**2 + 3*x + 1)

[OUT]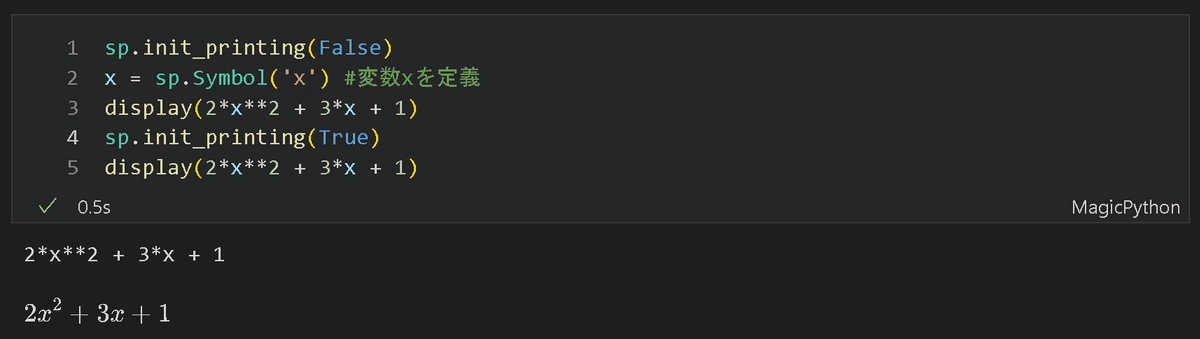

２－３．関数の定義：Function()

　Sympyクラスの関数として定義する場合は"Function(<関数名>)"を使用します。この関数は後述する微分などで使用していきます。

[IN]
x = sp.Symbol('x')
f = sp.Function('f')

print(type(f))
display(f)
display(f(x))

[OUT]
<class 'sympy.core.function.UndefinedFunction'>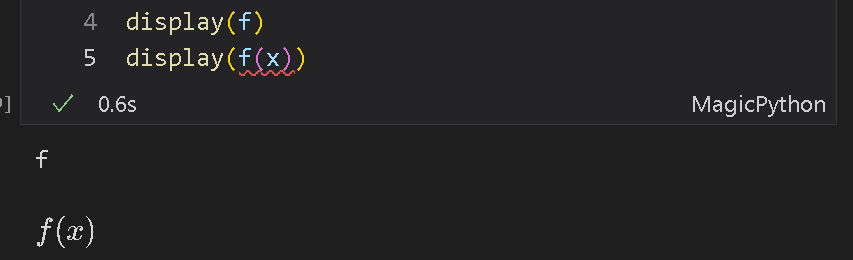

　またPythonでの関数式を作成して引数にSymbolを渡すとSymbol表示での数式を出力します。

[IN]
def func(x):
    return 10*x

x = sp.Symbol('x')
display(func(x))
display(func(10))

[OUT]
10x
100

２－４．基本的な定数：π, e, ∞, i

　Sympyでは数学で使用される各種定数を属性のAPIで呼び出せます。

[IN]
pi = sp.pi #円周率π
inf = sp.oo #無限大
Napier = sp.E #ネイピア数e
imagin_n = sp.I #虚数単位i

pi, inf, Napier, imagin_n

[OUT]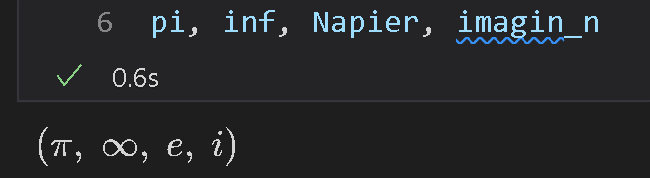

２－５．定数の小数化：sympy.Float()

　前節の定数を小数点として使用するには"sympy.Float(<変数>, <桁数>)"を使用します。なおSympyでのFloat変換はSympyクラスとなります。

[IN]
pi = sp.pi #円周率π

print(type(pi))
display(2*pi)

print(type(sp.Float(pi)))
display(2*sp.Float(pi))

[OUT]
<class 'sympy.core.numbers.Pi'>
2π

<class 'sympy.core.numbers.Float'>
6.283185307179596.28318530717959

[IN]
num1 = sp.Float(pi, 32)
num2 = float(pi)

print(f'Sympy: {type(num1)}, float(): {type(num2)}')
print(num1)

[OUT]
Sympy: <class 'sympy.core.numbers.Float'>, float(): <class 'float'>
3.1415926535897932384626433832795

３．操作の応用編

３－１．出力を非表示：symbol;

　出力を非表示にする場合は変数の直後に";(セミコロン)"をつけます。

[IN]
x = sp.Symbol('x')
x;

[OUT]
つけた場合は表示されない。なお”display(x;)”のような記法はSyntaxErrorになる

３－２．前の出力結果参照：_

　前回出力した結果を参照する場合は”_(アンダースコア)”を使用します。

[IN]
x = sp.Symbol('x')
print(x, type(x))
x = 100

print(x)
print(_)
print(type(x), type(_))

[OUT]
x <class 'sympy.core.symbol.Symbol'>

100
100
<class 'int'> <class 'int'>

４．数式の作成・整理

４－１．数式の作成

　Sympyで数式を作成するにはSympyのsymbolメソッドで定義した変数でPythonの記法通りに演算式を記載します。
　方程式の作成方法は追って紹介するEq()メソッドを使用します。

[IN]
x, y = sp.symbols(" x y ") #変数x, yを定義
eq = (x + y)**2
eq

[OUT]

４－２．数式の展開：expand()

　作成した数式を展開したいときは"expand(<数式>)"を使用します。

[IN]
sp.expand(eq)

[OUT]
※display(eq)で展開前の数式も表示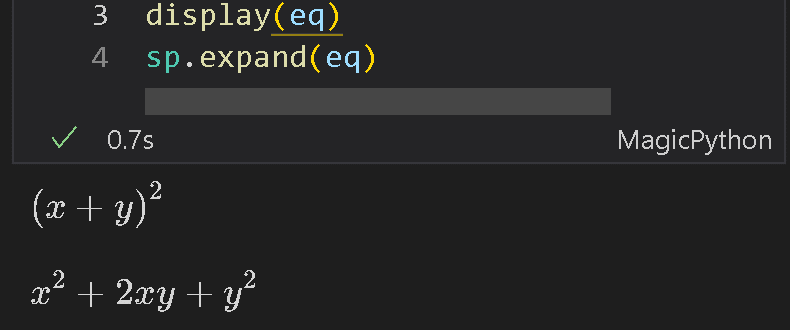

　引数"trig=True"を渡すと後述するtrigsimpと同じ簡単化の処理ができます。

[IN]
s = sp.expand((sp.cos(3*x)))
s_trig = sp.expand((sp.cos(3*x)), trig=True)

display(s), display(s_trig)
display(sp.simplify(s_trig))

[OUT]
Trigをつけないと展開されない。また展開した式はsimplify()でもとに戻る。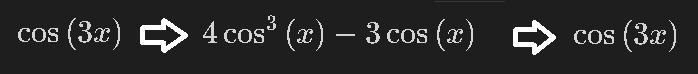

４－３．変数をまとめる：collect()

　展開された数式に対して特定の変数でまとめたい場合は"collect(<数式>)"を使用します。

[IN]
eq2 = sp.expand((x + y + 1)**2)

display(eq2)
sp.collect(eq2, x) #式をxで集める

[OUT]
※2xyと2xは一つのxとしてまとめることができる

４－４．因数分解：factor()

　因数分解（和や差の式を「積の式」に変形）するには"factor(<数式>)"を使用します。先ほど展開した数式を元に戻してみます。

[IN]
sp.factor(eq2) #因数分解

[OUT]

４－５．係数の抽出：coeff()

　数式の係数（$${ax+b}$$では$${x}$$の0乗係数はb, 1乗係数はa）を抽出するには"coeff(<変数>, <乗数>)"を実行します。

[IN]
display(eq2)
display(eq2.coeff(x, n=0)) #xの0乗の係数を取得
display(eq2.coeff(x, n=1)) #xの1乗の係数を取得
display(eq2.coeff(x, n=2)) #xの2乗の係数を取得
display(eq2.coeff(x, n=3)) #xの3乗の係数※存在しないため0

[OUT]

４－６．部分分数への展開：apart()

　分数を部分分数に展開するにはapart()を使用します。

[IN]
eq3 = 3/(x**3 - 1)
eq_apart = sp.apart(eq3)

display(eq3)
display(eq_apart)
[OUT]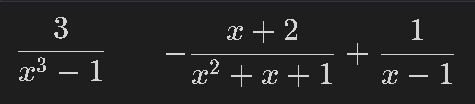

４－７．簡易化：simplify()

　数式を簡素化（綺麗にまとめる）にはsimplify()を使用します。

[IN]
display(eq_apart)
display(sp.simplify(eq_apart)) #分数を簡単にする

[OUT]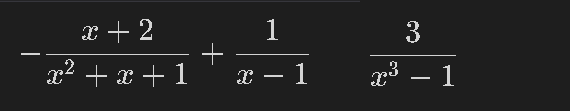

５．基本的な計算

５－１．数値の代入（上書き）

　symbolで定義したままだと記号で出力されますが、値を渡したい場合はPython記法通りに変数に対して数値を渡します。
　この方法では変数は上書きされるため一時的に値を代入する場合は後述のsubs()メソッドを使用します。

[IN]
a = sp.Symbol('a')
display(a)
a = 100
a

[OUT]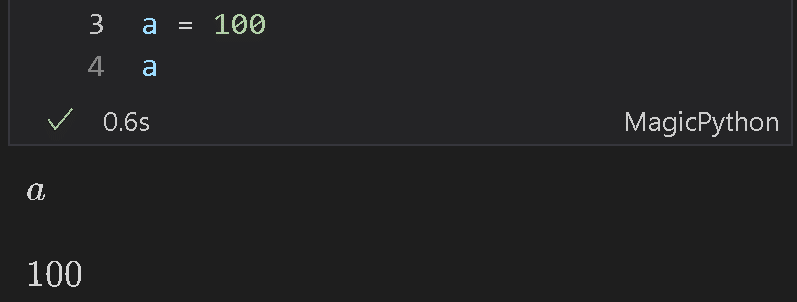

５－２．一時的な数値代入：subs()

　変数や数式に一時的に数値を代入したい場合は”subs(<変数>, <値>)"を使用します。下記の通りsubs()実行後の数式に変化はありません（上書きされていない）。
　また複数の変数に値を渡す場合は"[(<変数1>, <値1>), (<変数２>, <値２>)・・・]"のようにリストの中に変数と値をタプルで渡します。

[IN]
def func(x, y):
    return x**2 + y**2

x, y = sp.symbols('x y')
f1 = func(x, y)
display(f1.subs(x, 2))
display(f1)

[OUT]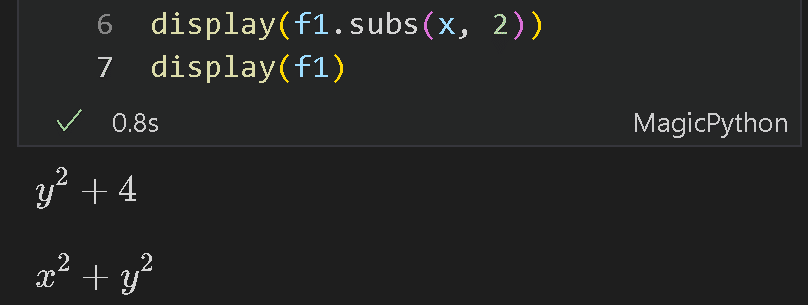

[IN]
f1.subs([(x, 2), (y, 3)])

[OUT]
13

５－３．分数：Rational()

　計算値を小数点ではなく分数で表したい場合は"Rational(<分子>, <分母>)"とします。Rational()で定義された変数で計算したものは分数として出力されます。

[IN]
quater = sp.Rational(1, 4)
print(type(quater))


display(1/4)
display(quater)
display(quater+7)

[OUT]
<class 'sympy.core.numbers.Rational'>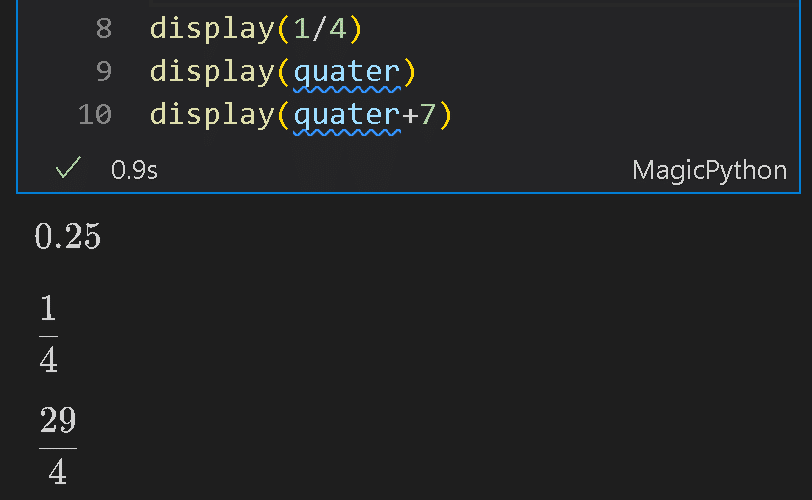

６．基本的な関数

６－１．基礎関数：log, exp, sin, cos

　Sympyでは様々な関数が使用できます。一部を下記に抜粋しました。

【関数一覧】
●sp.log(x) #対数log
●sp.codegen.cfunctions.log10(x)：$${\log_{10}}$$
●sp.exp(x) #指数exp
●sp.sin(x) #正弦sin
●sp.cos(x) #余弦cos
●sp.tan(x) #正接tan
●sp.cot(x) #余接cotangent
●sp.sec(x) #正割secant

[IN]
eq_sqrt = sp.sqrt(x) #平方根sqrt
eq_exp = sp.exp(x) #指数exp
eq_log = sp.log(x) #対数log
eq_abs = sp.Abs(x) #絶対値abs
eq_sin = sp.sin(x) #正弦sin
eq_cos = sp.cos(x) #余弦cos
eq_tan = sp.tan(x) #正接tan
eq_cot = sp.cot(x) #余接cotangent
eq_sec = sp.sec(x) #正割secant

eq_sqrt, eq_exp, eq_log, eq_abs, eq_sin, eq_cos, eq_tan, eq_cot, eq_sec

[OUT]

【参考例】
　解に虚数が入る可能性がある場合はSymbolに"real=True"を渡します（下記の通りそのままだと$${|x|}$$ではなく$${\sqrt{x^2}}$$になる）。

[IN]
x = sp.Symbol('x')
display(sqrt(x**2))
x = sp.Symbol('x', real=True) #実数のみ
display(sqrt(x**2))

[OUT]

　log↔expの変換も自動で実施してくれます。

[IN]
a=sp.Symbol("a")

display(sp.exp(sp.log(a)))
display(sp.log(sp.E**2))

[OUT]
a
2

$$
e^{\ln a} = a
$$

$$
\log e^2 = 2 \log e = 2
$$

６－２．三角関数の位相

　三角関数では位相$${\theta}$$が使用され弧度法（ラジアン）で計算されます$${2\pi=360^{\circ}}$$。角度で計算したい場合はRational()を使用してラジアンを角度に変換する係数$${\frac{\pi}{180}}$$をかけます。

[IN]
def degrad(x):
    return sp.Rational(x, 180)*pi

sin1 = sp.sin(sp.pi/3) #π/3=60°
sin2 = sp.sin(sp.Rational(60, 180)*pi) #角度をラジアンに変換
sin3 = sp.sin(degrad(60)) #sin2と同じ
display(sin1, sin2, sin3)

[OUT]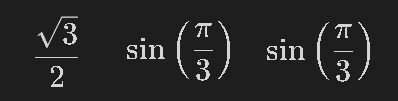

６－３．三角関数を含む数式の簡単化：trigsimp()

　三角関数や双曲線関数を含む式の簡単化には trigsimp()を使用します。

$$
\cos^2 x - \sin^2 x=\cos(2x)
$$

[IN]
x = sp.Symbol('x')
sp.trigsimp(sp.cos(x)**2 - sp.sin(x)**2)

[OUT]
cos(2x)

６－４．テイラー展開：series()

　テイラー展開とは特定の関数$${f(x)}$$に対して別の形に置き換えた近似式を作成する計算だったと思います（十分に理解できていないためURL張っておきます）。

　テイラー展開は"series(<数式>, <変数>, <展開点>, <展開項数>)"で計算でき、最後の展開項数nに合わせてn次のテイラー展開を計算します。

[IN]
x = sp.Symbol('x', real=True)
sp.series(sp.sin(x), x, 0, 6) #sin(x)の0から6次までのテイラー展開

[OUT]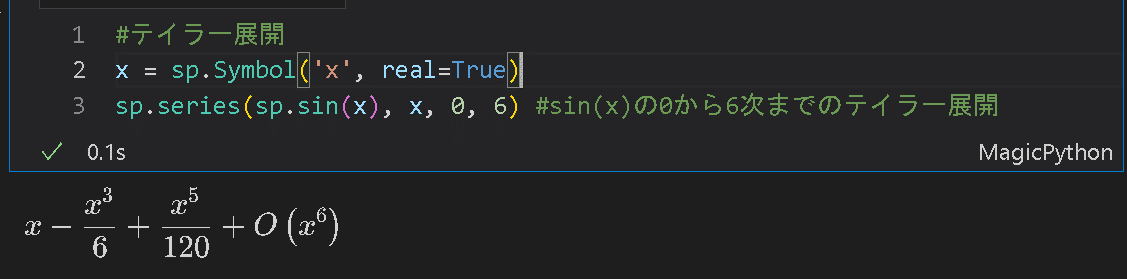

７．数列・順列

　数列の計算を説明します。説明がない限り数列の記号は下記を使用します。

$$
数列\lbrace a_n\rbrace：a_1,a_2,a_3,a_4,\cdots,a_n,\cdots
$$

$$
a_1 第1項(初項)\\ a_2 第2項\\ \vdots\\ a_n 第n項(n個の数列なら末項)\\
$$

７－１．数列の総和：summation

　数列の和は"summation(一般項 a_i, (i, 初めの i, 最後の i))"です。

$$
\sum_{k=1}^na_k=a_1+a_2+a_3+\cdots+a_n
$$

下記では$${\sum_{i=1}^{10} i^2}$$を計算しました。

[IN]
i = sp.Symbol('i')
sp.summation(i**2, (i, 1, 10))

[OUT]
385

　$${i^2}$$における N個までの数列の和は下記の通りです。この解はsummationで計算後にfactor()で因数分解することにより取得できます。

$$
\sum_{i=1}^{N} i^2 = \frac{N (N+1)(2 N + 1)}{6}
$$

[IN]
N = sp.Symbol('N')
sum_square = sp.summation(i**2, (i, 1, N)) #1からNまでの和
display(sum_square)
sp.factor(sum_square) #因数分解

[OUT]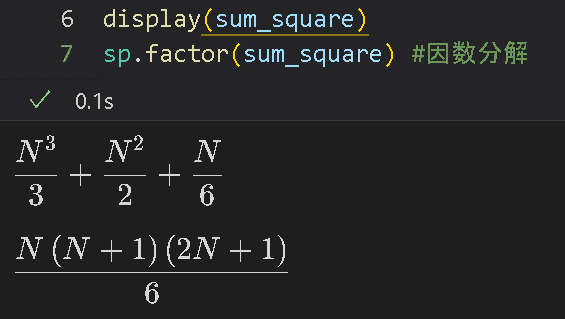

【注意点：summationでのindex】
　等差数列で再説明しますがsummationで入力する初項、末項のindexはPythonリストのスライスとは動きが違うことに注意が必要です。下記の通り初項=1, 末項=3を入力したらindex=1起点で3つの値が抽出されます。

[IN]
i = sp.Symbol('i')
print(sp.summation(i**2, (i, 1, 3)))
print(np.sum([1, 4, 9]))

[OUT]
14
14

７－２．数列の総乗：product

　数列の積は"product(一般項 a_i, (i, 初めの i, 最後の i))"です。

$$
\prod_{k=1}^{n}a_k=a_1\times a_2\times a_3\times \cdots\times a_n
$$

　コードでは$${a_k=x+1}$$を計算しました。summation同様に指定するindexの値には注意が必要です。

$$
\prod_{k=1}^{n}a_k=\prod_{k=1}^{5}(x+1)=1\times2\times3\times4\times5=120
$$

[IN]
i = sp.Symbol('i')

total_pro = sp.product(i+1, (i, 0, 4)) #1~5の積
print(f'解の計算：{np.arange(1, 6).prod()}') #array([1, 2, 3, 4, 5])の積
print(total_pro)

pro_calc = sp.product(i+1, (i, 0, N))
display(pro_calc)

[OUT]
解の計算：120
120

(N+1)!

７－３．等差数列：sequence

　等差数列とは「初項aに一定の数（公差）dを次々に加えていってできる数列」のことを言います。一般解は下記通りです。

$$
等差数列：a_n = a + (n-1)d
$$

$$
等差数列の和S_n=\frac{1}{2}n\lbrace2 a+(n-1)d\rbrace
$$

　Sympyでは"sequence(<反応式>)"で計算でき、等差数列の解は"formula"属性で確認できます。
　等差数列の合計を計算したい場合はsummationと合わせて実行します。

[IN]
n = sp.Symbol("n")
num_seq = sp.sequence(3*n+1) #等差数列

print(num_seq, type(num_seq))
display(num_seq) 
display(num_seq[0:2]) #スライスで値を抽出
display(num_seq.formula) #数列の公式表示

total1 = sp.summation(num_seq.formula, (n, 0, 9))
total2 = sp.summation(num_seq.formula, (n, 1, 10))
print(total1, total2)

[OUT]
SeqFormula(3*n + 1, (n, 0, oo)) <class 'sympy.series.sequences.SeqFormula'>

[1,4,7,10,…]
[1, 4]
3n + 13n+1

145 175

【注意点：summationでの初項・末項のindex】
　等差数列の合計を計算する場合、下記ルールが適用されます。

等差数列(formula)で出力される式の初項のindexは0
summationは初項と末項のindex指定のため「項数n=末項-初項+1」

　summationのindexは"指定したindex分だけデータを抽出する"仕様です。よって通常Pythonスライス：[0:9]だとlen()=9であり末項は[8]ですがsummationでは[9]となります。「数列式に合わせて1開始で入力したり、スライスの分だけ末尾indexを増やすと項がずれる」ため注意が必要です。

$$
a_1,a_2,a_3,a_4,\cdots,a_n,\cdots=[1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31]\\
S_{n1}=\frac{1}{2}10\lbrace2\times 1+(10-1)3\rbrace=5\times(2+27)=145\\
S_{n2}=\frac{1}{2}10\lbrace2\times 4+(10-1)3\rbrace=5\times(8+27)=175
$$　

７－３．等比数列

　等比数列とは「初項aに一定の数（公比）rを次々に加えていってできる数列」のことを言います。一般解は下記の通りです。

$$
等比数列：a_n = ar^{n-1}
$$

　メソッドが見当たらなかったため作成する場合は自作関数を作成します。

[IN]
def multiplication(a, r, n):
    n_sym = sp.Symbol("N") #項数
    r_sym = sp.Symbol("r") #公比
    a_sym = sp.Symbol("a0") #初項
    
    n_calc = n-1 #変数を代入
    total = a*sp.product(r, (n_sym, 1, n_calc)) #等比数列の和
    return  total

multiplication(a=1, r=2, n=5)

[OUT]
16

７－４．階乗：factorial()

　階乗$${n!}$$の計算は”factorial(<nの数>)”とします。1つ飛ばしの階乗を計算したい場合は"factorial2"を使用します。

[IN]
sp.factorial(4)

[OUT]
24

$$
4! = 4\times 3\times 2\times 1 = 24
$$

[IN]
sp.factorial2(5)

[OUT]
15

$$
5!! = 5\times 3\times 1 = 15
$$

８．微分（differential）

　微分とは「関数$${f(x)}$$に対して微小区間（刻み幅）hにおける$${f(x)}$$の傾き」を意味します。

$$
f'(x)=\lim_{h \to 0} \frac{f(x+h)-(x)}{h}
$$

８－１．微分計算：Derivative／diff()

　微分を計算する場合は下記を使用します。

【微分の計算】
●diff(<数式>,<変数>, <微分の階数>)：微分の計算から表示まで一括処理
●Derivative(<数式>,<変数>)：微分の記号を付けた式を表示->"doit()"メソッドで計算を実行

[IN]
x = sp.Symbol('x')
eq = x**3 + 5*x + 2 #x^3 + 5x + 2
sp.diff(eq, x) #微分

s_d = sp.Derivative(eq, x) #微分式
s_d_doit = s_d.doit() #微分処理

display(s_d), display(s_d_doit)

[OUT]

８－２．n階微分：diff(n)

　n階微分する場合はdiffに微分の階数を渡します。

[IN]
sp.diff(eq, x, 2) #2階微分

[OUT]
６

８－３．極限：limit()

　極限を求めるには"limit(<式>, <変数>, <極限の値>)"を使用します。

$$
\displaystyle \lim_{x \to 0} \frac{sin x}{x} =1
$$

[IN]
x = sp.Symbol('x')
sp.limit(sp.sin(x)/x, x, 0) #極限

[OUT]
1

　微分の理論計算も実施できました。参考例として$${f(x)=x^2}$$から$${\frac{d}{dx}f(x)}$$を求めます。

$$
\lim_{x \to 0}\frac{d}{dx}f(x)=\lim_{x \to 0}\frac{(x+h)^2-x^2}{h}
$$

$$
\lim_{x \to 0}=\frac{(x^2+2hx+h^2)-x^2}{h}=\lim_{x \to 0}(2x+h)=2x
$$

[IN]
x = sp.Symbol('x')
h = sp.Symbol('h') #刻み幅h

sp.limit(((x+h)**2-x**2)/h, h, 0) #極限
[OUT]
2x

９．積分(integral)

　積分とは「関数$${f(x)}$$に対する$${f(x)}$$の面積」です。詳細として定積分で説明すると「関数$${f(x)}$$の定積分とは、区間a-bにおける微小区間$${dx}$$と高さ$${f(x)}$$による微小面積"f(x)dx"の合計値」です。

$$
\int_{b}^{a}f(x)
$$

９－１．積分：Integral()/integrate()

　積分式の作成は下記の通りです。

【微分の計算】
●integrate(<数式>, <積分する変数>)：積分の計算から表示まで一括処理
●Integral(<数式>,<変数>)：微分の記号を付けた式を表示->"doit()"メソッドで計算を実行

【計算時の注意点】
●積分定数Cは出力されませんC＝0扱いとなる）。

[IN]
eq = x**2 * sp.cos(x) + 2*x*sp.sin(x)
eq_integrate = sp.integrate(eq, x) #積分

display(eq)
display(eq_integrate)

[OUT]

[IN]
_s = sp.Integral(eq, x) #積分式
s = _s.doit() #積分処理
display(_s, s)

[OUT]

【参考：検算】
　上記の計算は部分積分を使用した非常にややこしいものですが正しい結果が得られました。念のために検算して間違いないこと確認しました。

$$
f(x) =x^2 \cos x + 2 x \sin x \\
\int f(x)dx=\int \left(x^2 \cos x + 2 x \sin x \right)\, dx
$$

$$
{f_{1}}{\left(x \right)} = x^{2}よりf'_{1}(x)=2x \\
{g_{1}}{\left(x \right)} = \cos{\left(x \right)}よりG_{1}(x)=\int g_{1}(x)=sin(x) \\
{f_{2}}{\left(x \right)} = 2 x よりf'_{2}(x)=2\\
{g_{2}}{\left(x \right)} = \sin{\left(x \right)}よりG_{2}(x)=\int g_{2}(x)=-cos(x)
$$

$$
\int (x^2 \cos x)dx = \int f_{1}(x)g_{1}(x)dx= f_{1}(x)G_{1}(x)-\int f'_{1}(x)G_{1}(x)dx \\
=x^2sin(x)-\int 2xsin(x)
$$

$$
\int \left(x^2 \cos x + 2 x \sin x \right)\, dx=\int \left(x^2 \cos x\right)\, dx+\int \left( 2 x \sin x \right)\, dx \\
=x^2sin(x)-\int 2xsin(x)+\int \left( 2 x \sin x \right)\, dx \\
=x^2sin(x)
$$

９－２．定積分

　定積分を実施する場合は変数の引数にタプルで"(<積分する変数>, <下の定数>, <上の定数>)"を渡します。

$$
\int_0^{\pi/2} \sin x \,dx = 1
$$

[IN]
sp.integrate(sp.sin(x), (x, 0, sp.pi/2))

[OUT]
１

９－３．数値積分：evalf()

　解析的に積分できない場合"integrate()"は値をそのまま返します。数値積分によって近似値を求めるには"evalf()"メソッドを使用します。

[IN]
sp.integrate(sp.sin(x), (x, 0, sp.pi/2))
s_int = sp.integrate(sp.sin(sp.sin(x)), (x, 0, sp.pi))

display(s_int) #理論解がないためそのままで出力
print(s_int.evalf()) #数値計算による近似値

[OUT]
1.78648748195005

　参考としてガウス積分も計算してみました。

$$
ガウス積分：\int^{\infty}_{-\infty}\exp(-ax^ 2)dx=\sqrt{\frac{\pi}{a}}
$$

[IN]
#ガウス積分
a, x = sp.symbols('a x')
sp.integrate(sp.exp(-a*x**2), (x, -sp.oo, sp.oo)) #e^(-ax^2)を無限区間で積分

[OUT]

１０．方程式／連立方程式

１０－１．方程式の作成：sp.Eq()

　方程式を作成するには"sympy.Eq(<左辺>, <右辺>)"を使用します。

[in]
x1, x2 = sp.symbols("x1 x2")

eq1 = sp.Eq(x1 + 2*x2, 1) 
eq2 = sp.Eq(3*x1 + 5*x2, 2)
display(eq1, eq2)

[out]
※まとめて下図参照

　方程式の片方を表示したい場合は{左辺：lhs、右辺：rhs}を属性として使用します。

[IN]
display(eq1.lhs, eq2.lhs)
display(eq1.rhs, eq2.rhs)

[OUT]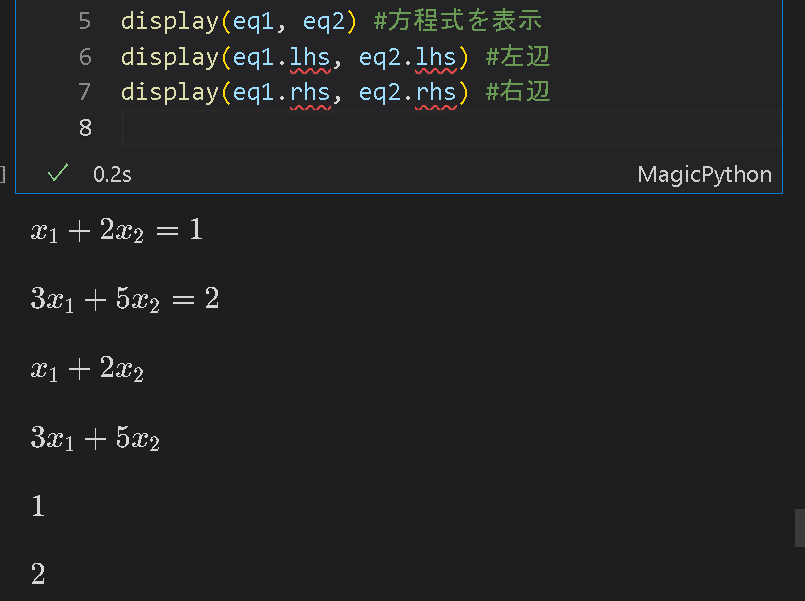

１０－２．代数方程式の解：solve()

　方程式f(x)=0の解を求めるには"solve(<方程式>, <変数>)"とします。出力はリストとして出力されます。リストのためスライスで抽出可能です。

[IN]
def func(x):
    return x**2 + 3*x + 2

sols = sp.solve(func(x), x)
print(type(sols))
print(sols)

[OUT]
<class 'list'>
[-2, -1]

１０－３．代数方程式の虚数解：real_roots

　$${x^3 = 8}$$のような方程式では虚数解が得られます。虚数解が不要な場合は"real_roots"を使用するかSymbol作成時に"real=True"を設定します。

[IN]
x1 = sp.Symbol('x1')
x_real = sp.Symbol('x', real=True)

display(sp.solve(x1**3-8))
display(sp.real_roots(x1**3 - 8))
display(sp.solve(x_real**3-8))

[OUT]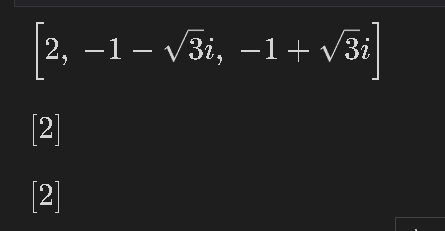

１０－４．連立方程式の解：solve()

　連立方程式も同様に"solve"を使用します。計算時は"solve(<[方程式のリスト]>, <[変数のリスト]>)"のように式と変数をリストで渡します。
　数式の渡し方としては①Eqで方程式を定義、②式を変形してf(x)=0の形で渡す　方法があります。

$$
x^2 + y^2 = 5\\
x + y =1
$$

[IN]
x, y = sp.symbols('x y')
eq1 = sp.Eq(x**2 + y**2, 5) #x^2 + y^2 = 5
eq2 = sp.Eq(x + y, 1) #x + y = 1
sp.solve([eq1, eq2], [x, y])

[OUT]
[(−1, 2), (2, −1)]

[IN]
sp.solve([x**2 + y**2 - 5, x + y -1], [x, y])

[OUT]
[(−1, 2), (2, −1)]

１０－５．方程式の数値解：evalf()/nsolve()

　$${f(x) = x^3 + 8 x -3}$$のように複雑な解をもつ場合は数値解として結果を取得します。取得は得られた解に対して”evalf()”メソッドを使用します。

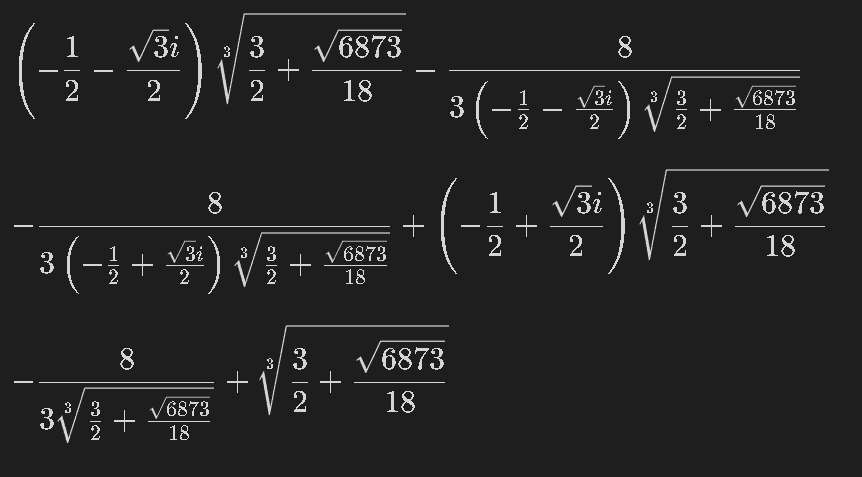
[IN]
def f(x):
    return x**3 + 8*x -3

sols = sp.solve(f(x))
print(type(sols), len(sols))

for idx, sol in enumerate(sols):
    print(f'解{idx+1}：', sol.evalf())

[OUT]
<class 'list'> 3

解1： -0.184366593784688 - 2.84639651537015*I
解2： -0.184366593784688 + 2.84639651537015*I
解3： 0.368733187569376

　多項式方程式でない場合は，nsolve 関数を使って数値解を探します。

[IN]
def g(x):
    return (x - 1)*sp.exp(x)

sols = sp.solve(g(x) - 1)
display(sols)
print(type(sols), len(sols)) #解は1つ

sp.nsolve(g(x) - 1, x, 1, prec=20)

[OUT]
[W(e^(−1))+1]
<class 'list'> 1
1.27846454276107379511.2784645427610737951

１０－６．常微分方程式の解：dsolve

【１階常微分方程式】
　常微分方程式の解を求めるには”dsolve”を使用します。解き方としては２パターンあります。

【dsolveの使い方】
●微分にDerivative使用：Eq(<Derivativeの式>, <右辺>)を使用して、解計算時にdsolve()に式と積分する変数の２つを渡す
●微分にdiff使用：Eq(<diffの式>, <右辺>)を使用し解計算時にdsolve()に式のみを渡す

$$
\frac{dy}{dx} = a yよりy{\left(x \right)} = C_{1} e^{a x}
$$

[IN]
x, a = sp.symbols('x a')
y = sp.Function('y')(x)
eq = sp.Eq(sp.Derivative(y, x), a*y)

display(eq)
display(sp.dsolve(eq, y))

[OUT]

[IN]
eq2 = sp.Eq(sp.diff(y, x), a*y)
sp.dsolve(eq2)

[OUT]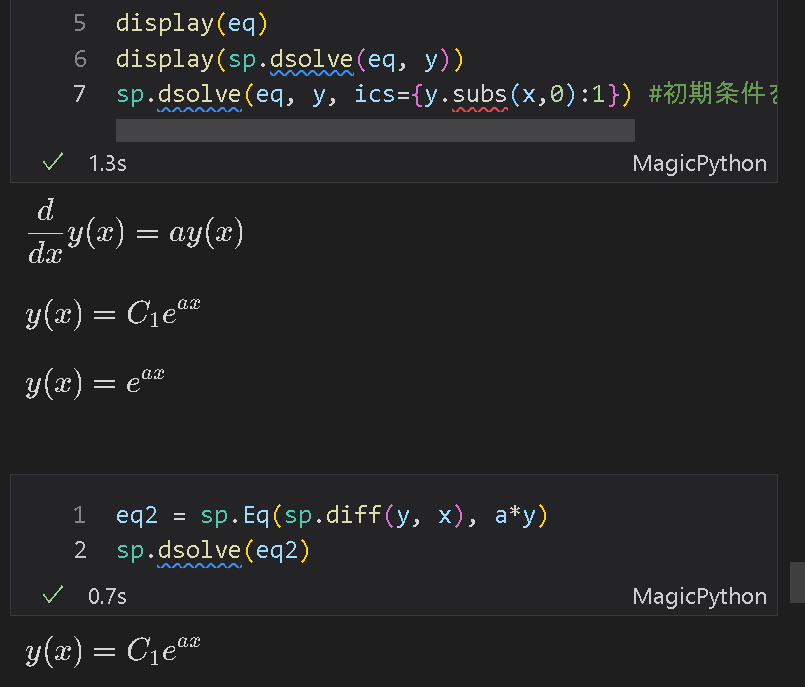

　上記の通り階には「（任意の）積分定数C」が出力されます。初期条件を”ics={...:...}”で渡すとCは任意に決まります。

[IN]
sp.dsolve(eq, y, ics={y.subs(x,0):1})

[OUT]
上記参照

【２階常微分方程式】
　２階微分も同様にdsolve()で計算できます。練習として下記を解きます。

$$
単振動の運動方程式：m\frac{d^{2}x}{dt^{2}}=-kx より \frac{d^{2}x}{dt^{2}}=-Kx
$$

$$
解：\displaystyle x{\left(t \right)} = C_{1} \sin{\left(\sqrt{K} t \right)} + C_{2} \cos{\left(\sqrt{K} t \right)}
$$

$$
時刻t=0における初期位置x=x_{0}, 初速度v=v_{0}での解：\displaystyle x{\left(t \right)} = x_{0} \cos{\left(\sqrt{K} t \right)} + \frac{v_{0} \sin{\left(\sqrt{K} t \right)}}{\sqrt{K}}
$$

x：移動距離、t：時間、m：物体の質量、K：比例定数

[IN]
t = sp.Symbol("t") #時間
K = sp.Symbol("K", positive=True) #ばね定数(正の値のみ)
x = sp.Function("x")(t) #位置
eq = sp.Eq(sp.Derivative(x, t, 2), -K*x) #運動方程式

display(eq)
display(sp.dsolve(eq, x))

#初期条件を指定
x0, v0 = sp.symbols("x0 v0")
sp.dsolve(eq, x, 
          ics={x.subs(t,0):x0,
               sp.diff(x, t).subs(t,0):v0})

[OUT]

１１．ベクトル／行列：配列の定義

　本章ではベクトル・行列を取り扱います。ベクトル・行列作成にはNumpyとの相性がよいためSympyと併用します。

１１ー１．ベクトル・行列の作成：Matrix()

　ベクトルや行列の作成は"Matrix"を使用します。リストで渡す必要があるためスカラーはなく、ベクトルは1次元配列、行列は2次元配列を渡すと作成できます。またベクトルはデフォルトでは列ベクトルが生成されます。
　値を抽出したいときは配列と同様のスライス操作で抽出や置換が可能です。
　配列作成時はNumpyを使用すると記載が楽になるためこれ以降ではNumpyのarrayを使って作成もします。

[IN]
import numpy as np

a1, a2, a3 = sp.symbols('a1 a2 a3', real=True) #実数のみ
vec_A = sp.Matrix([a1, a2, a3])

vec1 = sp.Matrix([1, 2, 3])
# vec2 = sp.Matrix([[1], [2], [3]]) #同上

mat1 = sp.Matrix([[1, 2], 
                  [4, 5]])

mat2 = sp.Matrix(np.arange(9).reshape(3, 3))

display(vec_A)
display(vec1)
display(mat1)
display(mat2)

print(vec1[0]) #1番目の要素
print(vec1[1:]) #1番目以降の要素

[OUT]
1
[2, 3]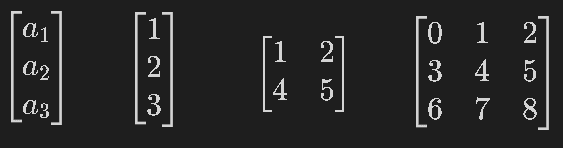

１１ー２．シンボルでの行列：MatrixSymbol()

　数値の行列ではなくSymbolでのMatrixを作成する場合は"MatrixSymbol()"でクラスを作成後に"Matrix(<作成したクラス>)"により作成します。
　出力後の値は前述の通りスライス操作で抽出・置換が可能です。

[IN]
w = sp.MatrixSymbol("w", 3, 3)
display(w), print(type(w))

W = sp.Matrix(w)
W

[OUT]
\displaystyle ww
<class 'sympy.matrices.expressions.matexpr.MatrixSymbol'>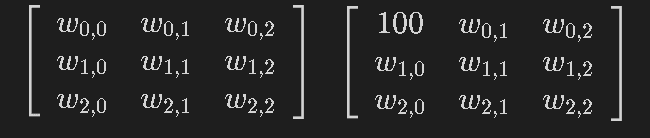

１１ー３．標準行列：eye, ones, zeros, diag

　各種行列は下記の通り作成できます。

【行列一覧】
●sp.zeros(ゼロ行列)：すべての値が0の行列を作成
●sp.ones(1行列)：すべての値が1の行列を作成
●sp.eye(単位行列)：対角成分のみ 1でそれ以外は 0である正方行列
●sp.diag(対角行列)：指定した数値で対角の値を埋めた行列

[IN]
M_eye = sp.eye(3)
M_ones = sp.ones(3)
M_zeros = sp.zeros(3)

display(M_eye, M_ones, M_zeros)

[OUT]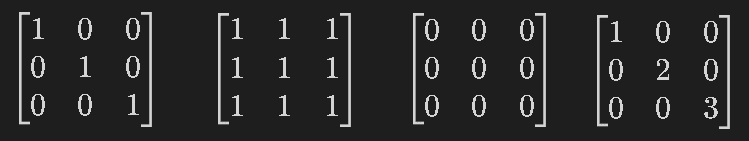

１１ー４．転置行列：transpose

　転置行列とは「行列の行と列を入れ替えた行列」です。Sympyでは"transpose"メソッドを使用しますが行列に"T"属性を渡しても同じ結果が得られます。

$$
\begin{pmatrix} a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} &a_{33}
\end{pmatrix}->
\begin{pmatrix} a_{11} & a_{21} & a_{31} \\
a_{12} & a_{22} & a_{32} \\
a_{13} & a_{23} &a_{33}
\end{pmatrix}
$$

[IN]
mat = sp.Matrix(np.arange(9).reshape(3, 3))

mat_Trans = sp.transpose(mat)
mat.T #sp.transpose(mat)と同じ

[OUT]
※転置行列、逆行列、行列式の結果をまとめて示す

１１ー５．逆行列：inv

　$${A}$$の逆行列$${A^{-1}}$$とは$${{\bf AA}^{-1} = {\bf I}}$$が成り立つ行列です（I：単位行列）。
　逆行列が存在しない行列もあるため今回か下記サンプルで計算しました。逆行列は"inv"メソッドで実行できますが"vec**(-1)"も同じ結果が得られます。

$$
\begin{bmatrix} 1 & 2 \\ 3 & 4 \\
\end{bmatrix}
\begin{bmatrix} -2 & 1 \\ 1.5 & -0.5 \\\end{bmatrix}
=\begin{bmatrix} (1×-2+2×1.5) & (1×1 + 2×-0.5) \\ (3×-2+4×1.5) & (3×1+4×-0.5) \\\end{bmatrix}
=\begin{bmatrix} 1 & 0 \\ 0 & 1 \\
\end{bmatrix}
$$

[IN]
sp.Matrix(np.arange(1,5).reshape(2,2)).inv()

[OUT]
Matrix([[-2, 1], 
　　　　[3/2, -1/2]])

[IN]
mat_2d = sp.Matrix(np.arange(1,5).reshape(2,2))
mat_2d**(-1)

[OUT]
Matrix([[-2, 1], 
　　　　[3/2, -1/2]])

１１ー６．行列式：det()

　行列式は下記記事ご参照ください。計算は”det”を使用します。

[IN]
mat.det()

[OUT]
0

１２．ベクトル／行列：配列同士の計算

１２ー１．四則演算

　Pythonの四則演算で計算した結果は下記の通りです。割り算は別のメソッドを使用しないとエラーが発生します。

[IN]
vec1 = sp.Matrix([[1, 2],
                 [3, 4]])
vec2 = sp.Matrix([[10, 20],
                  [30, 40]])

vec_add = vec1 + vec2 #要素ごとの足し算
vec_sub = vec1 - vec2 #要素ごとの引き算
vec_mat = vec1*vec2 #内積

display(vec_add)
display(vec_sub)
display(vec_mat)

[OUT]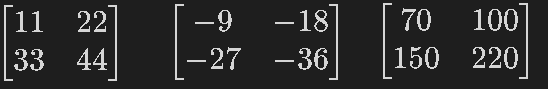

１２ー２．1次元の内積：dot()

　１次元ベクトルの内積はdot()を使用しますが注意事項は下記の通りです。

【内積の注意事項】
●ベクトルの内積はvec1.dot(vec2)で計算できる
●行列のの内積を計算する場合は”*”を使用すること。dotで計算すると1次元化されるため欲しい結果は得られない。
　ー＞詳細は「https://github.com/sympy/sympy/issues/13815」参照
●1次元ベクトルを”*”で計算する場合は行列定義の通り要素数を合わせる必要があり、sp.Matrix()では列ベクトルのため行ベクトルへの変換が必要

[IN]
A, B = sp.Matrix(sp.symbols('a1:4')), sp.Matrix(sp.symbols('b1:4'))

display(A.dot(B))
display(A.T*B) #行ベクトル×列ベクトルしないとエラー
vec1.dot(vec2) #内積

[OUT]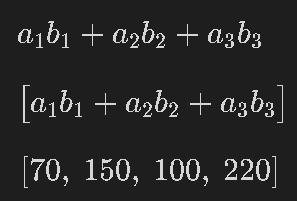

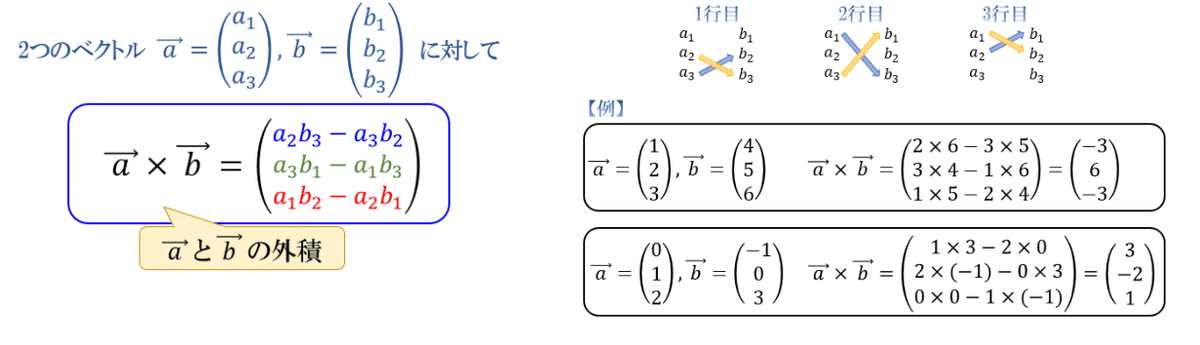
１２ー３．外積：cross()

　ベクトルの外積は"cross"メソッドを使用します。

$$
\displaystyle [ \boldsymbol{a} , \boldsymbol{b} ] = \boldsymbol{a} \times \boldsymbol{b} = \sum_{j,k} \varepsilon_{ijk} a_j b_k
$$

[IN]
A, B = sp.Matrix(sp.symbols('a1:4')), sp.Matrix(sp.symbols('b1:4'))
A.cross(B) #外積

[OUT]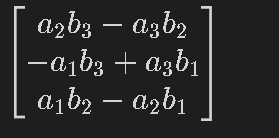

１２ー４．アダマール積：multiply_elementwise()

　内積は”*”ですがアダマール積は”multiply_elementwise”を使用します。

$$
A\bigodot B
$$

[IN]
vec1 = sp.Matrix([[1, 2],
                 [3, 4]])
vec2 = sp.Matrix([[10, 20],
                  [30, 40]])

vec1.multiply_elementwise(vec2) #アダマール積

[OUT]
Matrix([[10, 40], 
　　　　[90, 160]])

１２ー５．ベクトルの大きさ：norm()

　ベクトルの大きさ（長さ）を表すには"norm"を使用します。

$$
|\boldsymbol{a}| = \sqrt{\boldsymbol{a}\cdot \boldsymbol{a}}=\displaystyle \sqrt{a_{1}^{2} + a_{2}^{2} + a_{3}^{2}}
$$

[IN]
A = sp.Matrix(sp.symbols('a1:4', real=True))
A.norm() #ノルム

[OUT]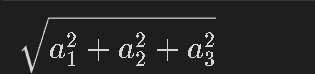

１２－６．グラムシュミットの直交化法：GramSchmidt()

　Sympyでは「グラムシュミットの直交化法」が計算できます。よく理解できていないので紹介のみです。

[IN]
vec1 = sp.Matrix([1,1,0])
vec2 = sp.Matrix([0,-1,1])
vec3 = sp.Matrix([1,1,1])

vecs = [vec1, vec2, vec3]
vec_GramS = sp.GramSchmidt(vecs) #グラムシュミット正規直交化
vec_GramS

[OUT]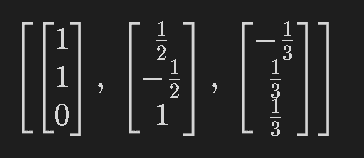

１３．グラフ作成

　Sympyを使用してグラフを作成します。グラフはMatplotlibベースで作成されており基本的な操作は下記記事をご確認ください。

１３－１．折れ線グラフ：plot

　$${y=f(x)}$$を$${a \le x \le b}$$範囲で折れ線グラフプロットするには"plot(f(x), (x, a, b))"となります。

[IN]
x = sp.Symbol("x")

sp.plot(sp.sin(x), (x, -sp.pi, sp.pi))

[OUT]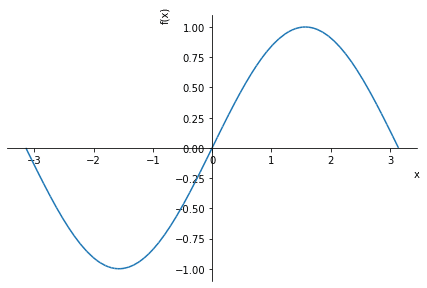

　体裁の調整はMatplotlibと同様の引数をplot()に渡します。

[IN]
sp.plot(sp.sin(x), (x, -2*sp.pi, 2*sp.pi),
     title='Fig.1 sin(x)',
     axis_center=(-2*sp.pi, -1),
     line_color='red',
     legend=True,
     xlabel='x_label',
     ylabel='y_label');

[OUT]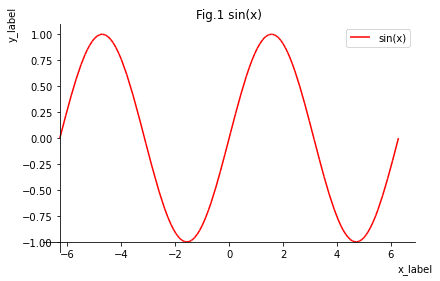

　Figの調整はMatplotlibの機能を使用して調整します。

[IN]
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] =12,8
plt.rcParams['font.size'] = 20

sp.plot(sp.sin(x), (x, -2*sp.pi, 2*sp.pi),
     title='Fig.1 sin(x)',
     axis_center=(-2*sp.pi, -1),
     line_color='red',
     legend=True,
     xlabel='x_label',
     ylabel='y_label');

[OUT]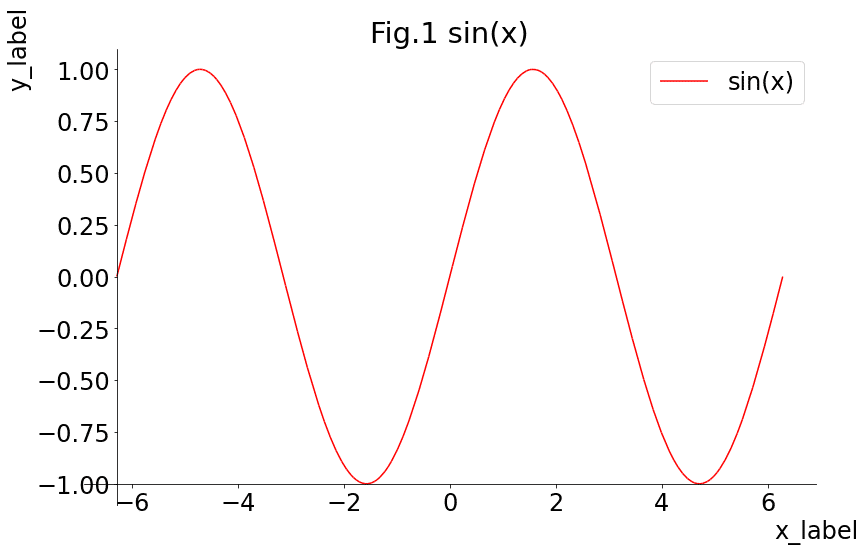

１３－２．３次元グラフ：plot3d

　３次元グラフを作成には別モジュールから"plot3d"をインポートします。

[IN]
from sympy.plotting import plot3d
x, y = sp.symbols('x y') #変数 x, y を初期化

plot3d(x*sp.sin(y), (x, -3, 3), (y, -4, 4), xlabel='x', ylabel='y')

[OUT]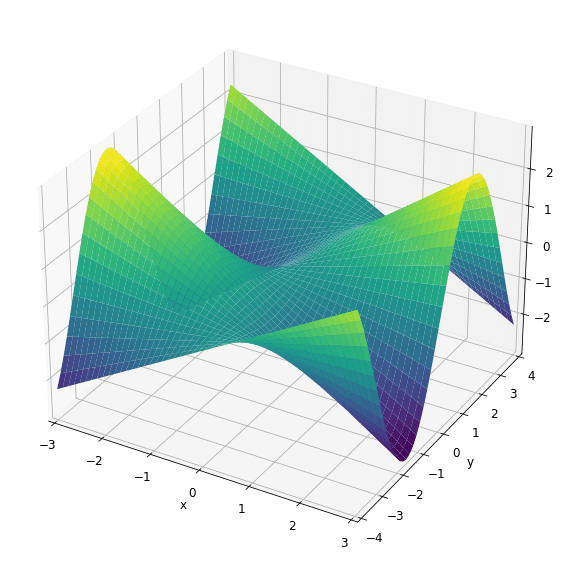

１４．コードの生成

１４ー１．C言語のコード生成：ccode()

　Sympyの数式からC言語のコード作成はccode()メソッドを使用します。

[IN]
x, y, z = sp.symbols(" x y z ")
print(sp.ccode(sp.exp(-x))) #C言語のコードに変換

[OUT]
exp(-x)

[IN]
np.random.seed(123)

x = sp.MatrixSymbol("x", 3, 1)
A = sp.Matrix(np.random.randint(15, size=(3,3)))
A_x = A * sp.Matrix(x)
display(A_x)

for i in range(3):
    code = sp.ccode(A_x[i], assign_to=f"y[{i}]")
    print(code)

[OUT]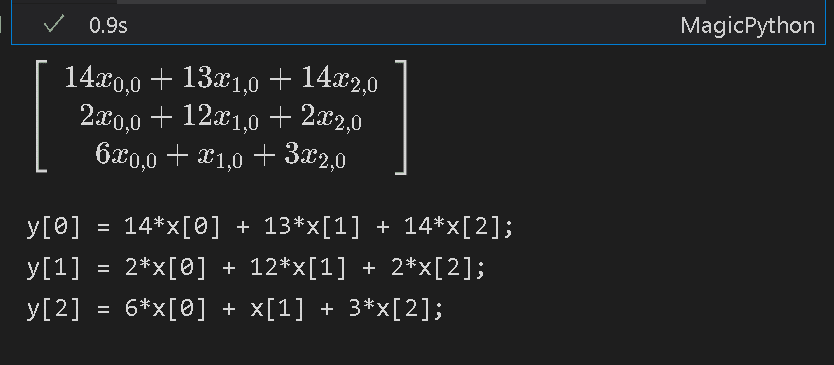

参考資料

あとがき

　Numpyと併用することでシミュレーションとかにうまく使えるかも。それにしても公式Docsが充実しているけど読みにくいな・・・・・
　あと数学は苦手意識そこまでなかったけど、だいぶ用語は忘れてるな・・・・

Pythonライブラリ(数式処理)：SymPy

１．概要

１－１．環境構築

２．Sympyの基本操作：各種変数の定義

２－１．変数の定義：シンボル作成

２－１－１．１つだけ定義：Symbol

２－１－２．まとめて定義：symbols

２－１－３．練習：LaTexによる表示

２－２．LaTeX版で表示：init_printing

２－３．関数の定義：Function()

２－４．基本的な定数：π, e, ∞, i

２－５．定数の小数化：sympy.Float()

３．操作の応用編

３－１．出力を非表示：symbol;

３－２．前の出力結果参照：_

４．数式の作成・整理

４－１．数式の作成

４－２．数式の展開：expand()

４－３．変数をまとめる：collect()

４－４．因数分解：factor()

４－５．係数の抽出：coeff()

４－６．部分分数への展開：apart()

４－７．簡易化：simplify()

５．基本的な計算

５－１．数値の代入（上書き）

５－２．一時的な数値代入：subs()

５－３．分数：Rational()

６．基本的な関数

６－１．基礎関数：log, exp, sin, cos

６－２．三角関数の位相

６－３．三角関数を含む数式の簡単化：trigsimp()

６－４．テイラー展開：series()

７．数列・順列

７－１．数列の総和：summation

７－２．数列の総乗：product

７－３．等差数列：sequence

７－３．等比数列

７－４．階乗：factorial()

８．微分（differential）

８－１．微分計算：Derivative／diff()

８－２．n階微分：diff(n)

８－３．極限：limit()

９．積分(integral)

９－１．積分：Integral()/integrate()

９－２．定積分

９－３．数値積分：evalf()

１０．方程式／連立方程式

１０－１．方程式の作成：sp.Eq()

１０－２．代数方程式の解：solve()

１０－３．代数方程式の虚数解：real_roots

１０－４．連立方程式の解：solve()

１０－５．方程式の数値解：evalf()/nsolve()

１０－６．常微分方程式の解：dsolve

１１．ベクトル／行列：配列の定義

１１ー１．ベクトル・行列の作成：Matrix()

１１ー２．シンボルでの行列：MatrixSymbol()

１１ー３．標準行列：eye, ones, zeros, diag

１１ー４．転置行列：transpose

１１ー５．逆行列：inv

１１ー６．行列式：det()

１２．ベクトル／行列：配列同士の計算

１２ー１．四則演算

１２ー２．1次元の内積：dot()

１２ー３．外積：cross()

１２ー４．アダマール積：multiply_elementwise()

１２ー５．ベクトルの大きさ：norm()

１２－６．グラムシュミットの直交化法：GramSchmidt()

１３．グラフ作成

１３－１．折れ線グラフ：plot

１３－２．３次元グラフ：plot3d

１４．コードの生成

１４ー１．C言語のコード生成：ccode()

参考資料

あとがき

いいなと思ったら応援しよう！

　２－１－１．１つだけ定義：Symbol

　２－１－２．まとめて定義：symbols

　２－１－３．練習：LaTexによる表示