
本当は面白い物理の授業 009 水平投射実践編
それでは、
「水平投射」の理解を深めるために、数値を入れて計算してみましょう。
前回の投降で、「水平投射」の概念を勉強しました。
その時、導き出された式が以下になります。

それでは実践です。
高い建物の屋上から、水平にボールを投射します。
その時の初速は20m/sです。
ボールがどの様な軌道を描くのか計算します。
また、空気抵抗は無視できるものとします。
最後にボールの位置を図示します。
よって、今回は有効数字は3桁としておきます。
(初期の鉛直方向の移動量の差を明確にするため)
重力加速もg=9.81(m/s^2)とします。
また、有効数字の考え方は別の授業で説明します。
t:経過時間
Vx : ボールの水平方向速度
Vy : ボールの鉛直方向速度
V : ボールの速度
X : ボールの水平方向移動量
Y : ボールの鉛直方向移動量
《ボールを投げ出した瞬間》
t = 0(s)
Vx = 20.0(m/s)
Vy = 0(m/s)
V = 20.0(m/s)
X = 0(m)
Y = 0(m)
《ボールを投げ出して0.5秒後》
t = 0.50(s)
Vx = 20.0(m/s)
Vy = 4.91(m/s) ←4.905
V = 20.6(m/s) ←20.59…
X = 10.0(m)
Y = 1.23(m) ←1.226…
《ボールを投げ出して1.0秒後》
t = 1.00(s)
Vx = 20.0(m/s)
Vy = 9.81(m/s)
V = 22.3(m/s) ←22.27…
X = 20.0(m)
Y = 4.91(m) ←4.905
《ボールを投げ出して1.5秒後》
t = 1.50(s)
Vx = 20.0(m/s)
Vy = 14.7(m/s) ←14.715
V = 24.8(m/s) ←24.83…
X = 30.0(m)
Y = 11.0(m) ←11.03…
《ボールを投げ出して2.0秒後》
t = 2.00(s)
Vx = 20.0(m/s)
Vy = 19.6(m/s) ←19.62
V = 28.0(m/s) ←28.01…
X = 40.0(m)
Y = 19.6(m) ←19.62
《ボールを投げ出して2.5秒後》
t = 2.50(s)
Vx = 20.0m/s)
Vy = 24.5(m/s) ←24.525
V = 31.6(m/s) ←31.64…
X = 50.0(m)
Y = 30.7(m) ←30.65…
《ボールを投げ出して3.0秒後》
t = 3.00(s)
Vx = 20.0(m/s)
Vy = 29.4(m/s) ←29.43
V = 35.6(m/s) ←35.58…
X = 60.0(m)
Y = 44.1(m) ←44.145
時間経過ごとにボールの「位置(X,Y)」と「速度」を図に描くと、下図のようになります。
Vx : 緑の矢印 ボールの水平方向速度
Vy : 青の矢印 ボールの鉛直方向速度
V : 赤の矢印 ボールの速度(合成した速度)

水平方向の速度は一定ですが、鉛直方向に加速します。よって、ボールの速度を表す赤矢印が段々と下を向いていきます。
〜〜〜〜〜〜〜〜〜〜〜〜〜〜
それでは、「水平投射」の実験してみましょう。
ここでは、
「ボールの落下位置」から「ボールの初速度」を算出してみます。
「ボール」と「タオル」を用意します。
野球やソフトボール用のボールが適しています。
できる限り空気抵抗の影響を受けないような重めのボールです。
机の横に「タオル」を敷きます。「タオル」の役目は、クッションです。無くても実験できますが、床が傷むかもしれません。
机の高さ(ボールが鉛直方向に落ちる距離)を測りましょう。
例えば、床から机の上面までの鉛直方向の距離が0.80mだとします。
次に、机の上のボールを転がして、床の上に落下させます。
「机の端」から「ボールが落下した位置」の水平距離を測ります。
例えば、この距離が0.20mだったとします。
Y = 1/2・g・t^2
t = √(2Y/g)
t = √(2✖️0.8/9.8)
= 0.40(s)
計算の結果、
ボールが床に落ちるまでの時間は0.40(s)です。
次に、水平方向の移動量から
X = Vx・t
Vx = X/t
Vx = 0.20/0.40
= 0.50(m/s)
初速は0.50(m/s)だったと推測できます。
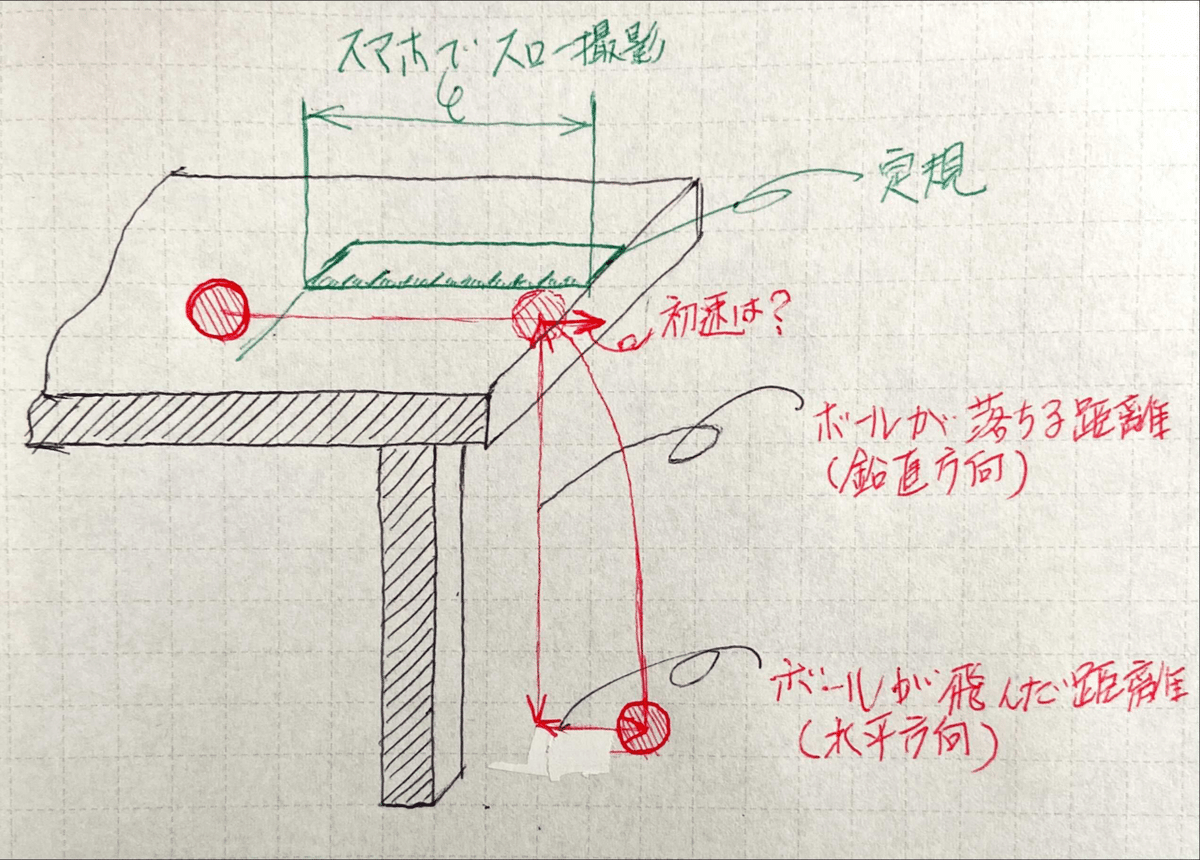
また、上記の実験と同時に、実際のボールの速度を測ってみましょう。
机の上に「定規📏」を置きます。その定規の横でボールを転がします。
スマホのスロー撮影機能で動画を撮ります。
ボールが机の上を移動する距離と時間から、ボールの速度が算出します。
ボールは机の上を転がりながら減速しています。よって、この方法で測定した速度より、実際に飛び出した瞬間の初速のほうが、やや小さくはなります。
「スマホの測定値からの計算結果(初速)」と「落下距離からの計算結果(初速)」を比べてみましょう。
もちろん、いくらか空気抵抗や測定誤差があります。
よって、完全には同じ値になりません。
しかし、近い値が出たのではないでしょうか。
「水平投射」の理解を深めることは出来たでしょうか。
本当は面白い物理の授業010へ続く。
