
【第7回】分散と標準偏差-前編
高等学校における統計教育と情報教育の有機的なつながりを考えていくシリーズの7回目で、今回は分散と標準偏差についてです。
平成30年公示の高等学校学習指導要領でも引き続き、「数学I」で扱われる内容になります。
(4)データの分析
データの分析について,数学的活動を通して,その有用性を認識するとともに,次の事項を身に付けることができるよう指導する。
ア 次のような知識及び技能を身に付けること。
(ア)分散,標準偏差,散布図及び相関係数の意味やその用い方を理解すること。
(イ)コンピュータなどの情報機器を用いるなどして,データを表やグラフに整理したり,分散や標準偏差などの基本的な統計量を求めたりすること。
(ウ)具体的な事象において仮説検定の考え方を理解すること。
イ 次のような思考力,判断力,表現力等を身に付けること。
(ア)データの散らばり具合や傾向を数値化する方法を考察すること。
(イ)目的に応じて複数の種類のデータを収集し,適切な統計量やグラフ,手法などを選択して分析を行い,データの傾向を把握して事象の特徴を表現すること。
(ウ)不確実な事象の起こりやすさに着目し,主張の妥当性について,実験などを通して判断したり,批判的に考察したりすること。
[用語・記号] 外れ値
数学Iと情報Iの関係
気になってくるのが、「数学I」と「情報I」の学習順序です。
「数学I」で分散・標準偏差や相関係数を教科書に沿って学び、「情報I」でコンピュータを利用してこれらの統計量を求めて分析するような流れが自然であると考えています。
一方で、数学の先生が授業の中で生徒に表計算ソフトを活用させながら、分散・標準偏差や相関係数の意味を伝えていくような授業も展開できるかと思います。
今回は後者を念頭において、記事を書いてみることにします。
四分位数と分散・標準偏差
四分位数が「中央値」をもとにしたデータの散らばり方の指標だったのに対して、分散は「平均値」をもとにしたデータの散らばり方の指標になります。したがって、本来は外れ値を含まないようなデータに対して使うことが有効です。次回の記事の中では四分位数を考えたときのデータと同じものを利用して比較もしてみたいと思います。
まずはシンプルなデータで
まずは、シンプルなデータを見ながら定義をします。
10名の生徒が数学と情報の5点満点の小テストを受けた結果を使ってみたいと思います。
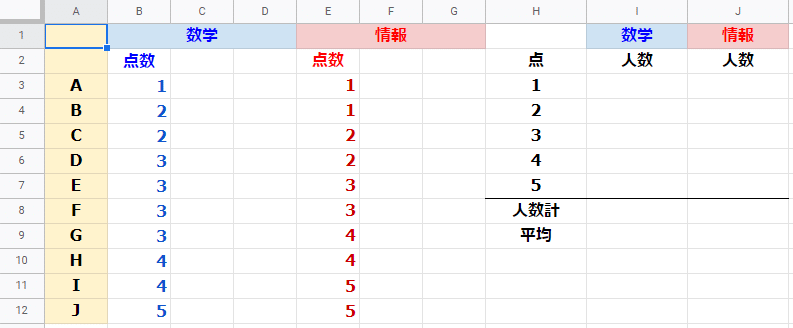
平均点を求める
まずは、平均点です。セルI9に数学の平均点、セルJ9に情報の平均点を出力させます。表計算ソフトのAVERAGER関数ですね。
セルI9 =AVERAGE(B3:B12)
セルJ9 =AVERAGE(E3:E12)
どちらも3が出力されます。平均点は3点です。
このことからも平均点だけみても、得点の分布はよく分からないわけです。
データの散らばりを可視化
それでは、次に得点分布をグラフで見てみましょう。このあたりから数学の授業でコンピュータを使う際に、情報の授業でどこまで教えられているのかという相互のカリキュラムの連関を意識することになります。
セルI3に =COUNTIF($B$3:$B$12,H3) を入力します。
セルB3~B12(10名の数学の得点)の中にある、H3(1点)の数を数えるという意味でした。
この数式をI4~I7にコピーすることも考えて、参照方式を決めます。相対参照と絶対参照の復習ですね。
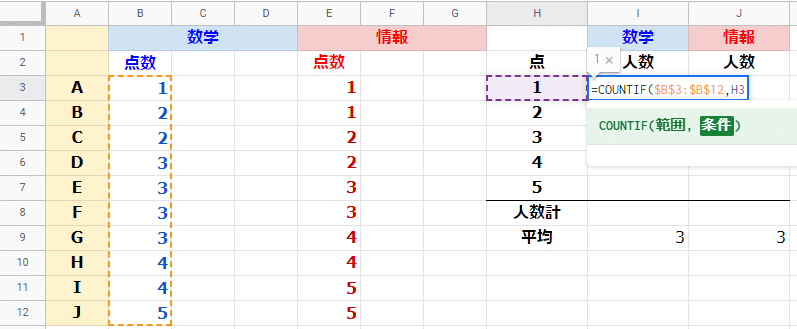
情報についても同様です。
セルJ3に =COUNTIF($E$3:$E$12,H3) を入力し、セルJ4~J7にコピーします。
あとで使う関係で、人数の合計も出しておきます。
セルI8 に =SUM(I3:I7) を入力し、セルJ8にコピーです。両方とも10が出力されます。COUNTIF関数に誤りがなさそうであることの確認にもなります。
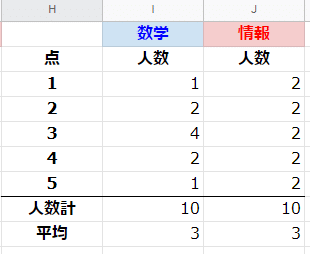
数学の得点分布の棒グラフを書いてみたいと思います。
Googleスプレッドシートでは、下記手順です。
(1) ヘッダ行を含めてデータ項目を選択(今回はH2:I7)
(2) メニューバーから[挿入]→[グラフ]を選択

(3) グラフエディタ
設定タブで次のように設定
グラフの種類:縦棒グラフ
系列から「点」を削除、X軸に「点」を追加
カスタマイズタブ
グラフと軸のタイトルのプルダウンからグラフと軸のタイトルをつける
(今回はグラフのタイトルを「数学の得点分布」としました)
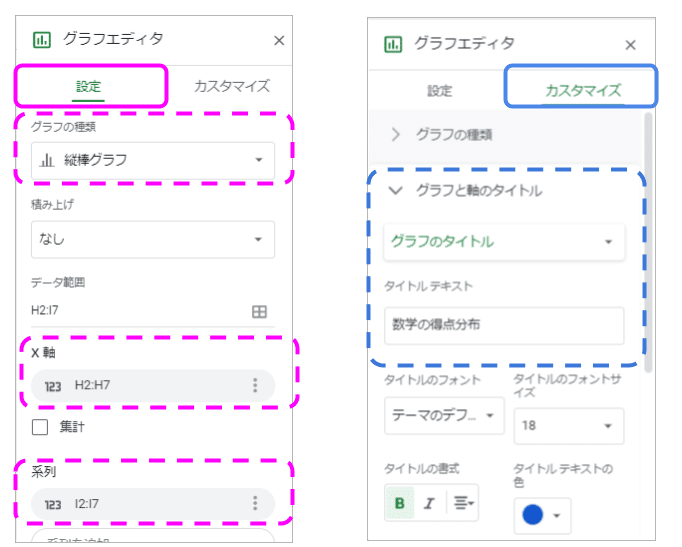
このようにして、数学と情報の小テストの得点分布の棒グラフを作成して並べてみました。

このようにしてみるとデータの散らばり方が分かりやすいですね。
数学のほうが平均点付近に値が集まっていることが分かります。
分散の定義
それではデータの散らばり方を見るには何に注目すればよいかを考えていくと、データの各値と「平均との差」に注目するのが自然であるという発想になります。その平均値との差の偏差といいます。
表計算ソフトで偏差を求めてみましょう。数学の平均点が入っているセルがI9でした。
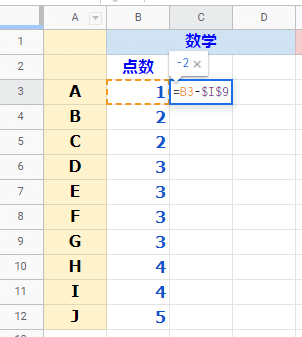
セルC3に = B3-$I$9 を入力して、セルC4~C12にコピーです。
情報についても同様の操作を行います。
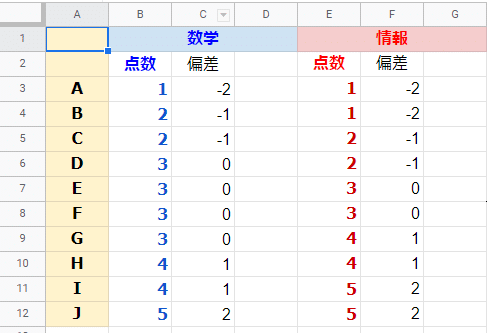
ここで、各データにおける偏差の合計はいつでも0になります。
これは平均の定義から明らかですが、文字式を使って説明すると下記のようになります。
$$
データ \ x_1,\ x_2, \cdots ,\ x_n \ の平均値 \quad m = \frac{x_1 + x_2, + \cdots + x_n}{n}
$$
なので、偏差の合計は、
$${(x_1 - m) + (x_2 - m) + \quad \cdots \quad + (x_n -m) }$$
$${=(x_1 + x_2 + \cdots + x_n) - nm}$$
$${= n \Bigl( \frac{x_1 + x_2 + \cdots + x_n}{n} - m \Bigl) = n(m-m) = 0}$$
となります。
したがって、「偏差の平均」は散らばり方を見るのには使えません。
そこで、偏差を2乗(平方)した値である偏差平方を使うことで、平均からの離れている程度をすべて0以上の数で表すことにします。偏差の絶対値を使う方法もあるのですが、平方の方がさまざまな計算を行いやすいことがその理由になります。
セルD3に = C3^2 を入力してセルC4~C12にコピー、その後、セルC3~C12をセルG3~G12にコピーします。(下図)
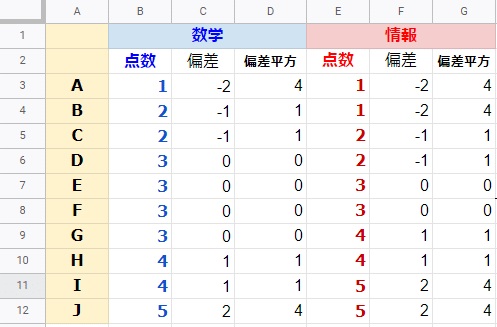
そして、この偏差平方の平均を取ったものが分散(variance)です。
それでは、セルI10に数学のデータの分散、セルJ10に情報のデータの分散を出力させてみましょう。
セルI10 = AVERAGE(D3:D12)
セルJ10 = AVERAGE(G3:G12)

分散は「偏差平方(=平均との差の2乗の値)の平均」でしたので、大きければ大きいほど、平均値から離れた値が多く、データが散らばっていると解釈します。従いまして今回の場合は、「情報のテストの点数の方が散らばりが大きい」と読み取れるわけです。
VAR.P関数とVAR.S関数
表計算ソフトで分散を求める関数も用意されています。
ただし、分散にはここで定義したもののほかに「不偏分散」と呼ばれているものがあり、求める関数が少し違います。
不偏分散については、もう少し先で記事を書きたいと思っていますが、今回はVAR.P関数を使うということを強調するに留めます。
なおPもSもついていないVAR関数は、以前のバージョン(Excelでは2007以前)と互換性を持たせるために使われるもので、VAR.S関数と同じ働きです。(なので、こちらも今回は使えません。)

比較のために、セルI11に =VAR.P(B3:B12)を、セルI12 =VAR.S(B3:B12) を入力して値を出力させてみました。
標準偏差
分散は「偏差平方(=平均との差の2乗の値)の平均」であるため、この例では点数を2乗しています。したがって、平均値の単位が「点」であるのに対して、分散の単位は「点^2」(平方点:点の2乗)になり単位がそろいません。これは次回の記事でその理由を書きますが、都合がよくありません。
そこで単位をそろえるために、分散の正の平方根をとった値である標準偏差(standard deviation)をよく利用します。
今回はSQRT関数を使って、分散の正の平方根を求めることにします。
セルI13に =SQRT(I10)を入力し、セルJ13にコピーします。
表計算ソフトで直接、標準偏差を求めるにはSTDEV.P関数を用います。
こちらについても上記のVAR.PとVAR.Sと対応しておりますので、この説明は割愛致します。
いったんまとめ
ここでは「情報I」の授業で表計算ソフトの演習をある程度行っていることを前提にし、数学の授業において生徒1人1台端末で表計算ソフトを利用しながら学習を進めていくようなことを想定して記事を書いてみました。
このあたりは学校によって、事情はさまざまだと思います。中高一貫校ですでに中学校3年生で「数学I」の内容を終えている場合などは、数学で学んだことの復習を「情報I」で行うような授業になるのかもしれません。
いずれにしましても、統計量の意味の理解とそれに基づいたデータの活用方法に対する生徒の学びを深まるためには、数学と情報のカリキュラムの連携が欠かせません。そしてさらに先には、そこで学んだデータ分析の手法を地歴科・公民科や理科などの授業、総合的な探究の時間の中で活かしていくことが望まれます。
このようにして、高等学校のカリキュラム全体の中でデータリテラシーを育てていく教育を目指していきたいというのが私の思いであります。
最後までお読みいただきありがとうございました。
次回は、標準偏差の意味を掘り下げ、データの標準化について考えてみたいと思います。
